MIMU辅助无人机相关干涉仪测向方法研究
王秋滢,匡春旭,钟万青
(哈尔滨工程大学信通学院,黑龙江 哈尔滨 150000)
1 引言
近年来,微型旋翼无人机测向技术被广泛应用于侦察、航海航空救援、抢险救灾等诸多领域,其优势在于旋翼无人机的悬停飞行能力可为测向系统提供良好的工作环境,避免了飞行位姿变化给测向系统带来的误差。然而微型旋翼无人机测向技术目前仍面临一些问题,无人机悬停状态下会因自身电机转动和气流影响而产生振动,使得与机体固连的阵列天线受角度干扰而产生相位误差,导致测向精度下降[1],直接影响无人机执行侦察和救援等任务的能力。
为保证机载测向系统在振动环境下的优良性能,关键在于对天线阵列的振动误差测量和校正,对此学者已经做了许多研究。文献[2,3]分析了振动对机载天线阵列的影响,确定振动对天线阵列的相位和幅度误差的影响,推导出共形天线失真的计算模型和相位噪声方程,并对其进行验证。在振动阵列校正方面[4-6],北约小组(NAOT)是较为知名的研究团队之一,他们采用机翼的一阶振动模式模拟测向天线阵列的结构形变,结合测向原理分析无人机振动对测向系统的影响,并利用自适应和合成波束成形法对误差进行补偿,在存在振动的情况下改进了到达方向估计。北约研究任务组SET-131则设计了一种具有主动振动补偿的天线阵列[7],用安装在天线附近的加速度计和压电陶瓷贴片的组合来感测变形,并诱导湮灭振动,可改善机载天线的抗振性能。除此之外,也有学者利用INS和万向节对误差进行测量和校正[8,9],用安装在天线平台背面的INS或载体自身INS测量其姿态信息,再通过万向节实时调节天线指向,达到校正天线相位误差的目的,但这种调节方式速度较慢,在高频振动条件下,难以进行校正。
针对上述问题,本文提出一种微型惯性测量单元(Miniature Inertial Measurement Unit,MIMU)辅助微型旋翼无人机强鲁棒性测向方法。首先,本文介绍了相关干涉仪测向原理,对微型旋翼无人机的振动形式进行建模,分析了无人机振动对测向系统的影响;其次,利用MIMU测量无人机的振动姿态角,在相关干涉仪测向原理的基础上,通过测得的振动姿态角对测向系统进行补偿;最后利用仿真验证该方法的有效性。实验结果表明该测向方法在微型旋翼无人机振动状态下有较好的测向精度。
2 基于相关干涉仪的微型无人机测向基本原理与误差分析
2.1 相关干涉仪测向原理及天线排布
目前测向体制种类众多,其中相关干涉仪测向体制适合机载测向在工程上的实现,其优点主要表现在以下几个方面:测向天线阵布阵方式灵活,可以根据飞行器的实际结构来确定天线安装的位置;可采用长短基线结合的方法来实现测向,并能保证一定的测向精度;测向原理简单,对信道的幅度及相位一致性要求较低。因此本文将在相关干涉测向系统的基础上进行分析与改进,本节首先简单介绍一维单基线相关干涉测向原理,单基线干涉仪测向原理图如图1所示。
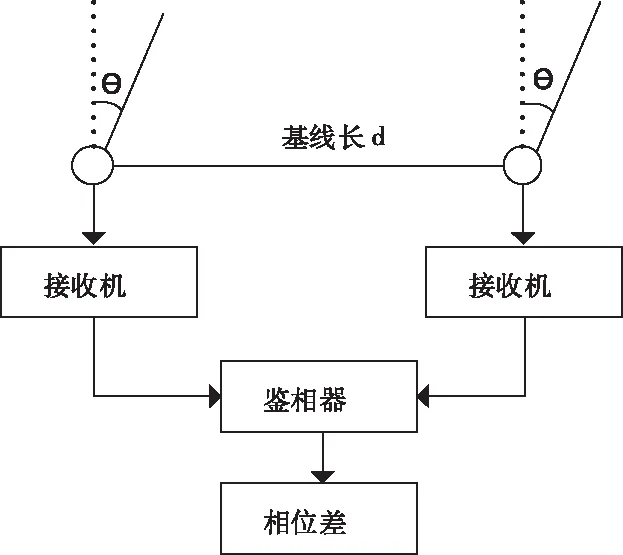
图1 单基线干涉仪测向原理图
来波信号从方位角θ射入两根天线,经接收机和鉴相器处理,得到两阵元间相位差Δφ为
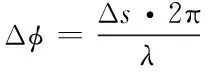
(1)
其中,波程差Δs=dsinθ,λ为来波信号的波长。
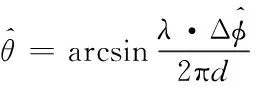
(2)
式(2)表示了来波方位角与相位差之间的数学关系。同理,在二维相关干涉系统中,来波方位角和仰角与相位差之间存在类似的对应关系,根据这种数学关系,以相等间隔分隔来波方位角和仰角,计算出每组方位角和仰角对应相位差的值,建立样本标准库。在测向时,天线间实测得到的相位差与样本标准库进行相关匹配运算,与实测相位差最接近的样本值所对应的方位角和仰角即为来波方向。为了提高相关匹配运算的准确性,相关干涉仪测向法通常采用多基线获取多个不同相位差,本文建立5天线均匀圆阵,天线排布图如图2所示。
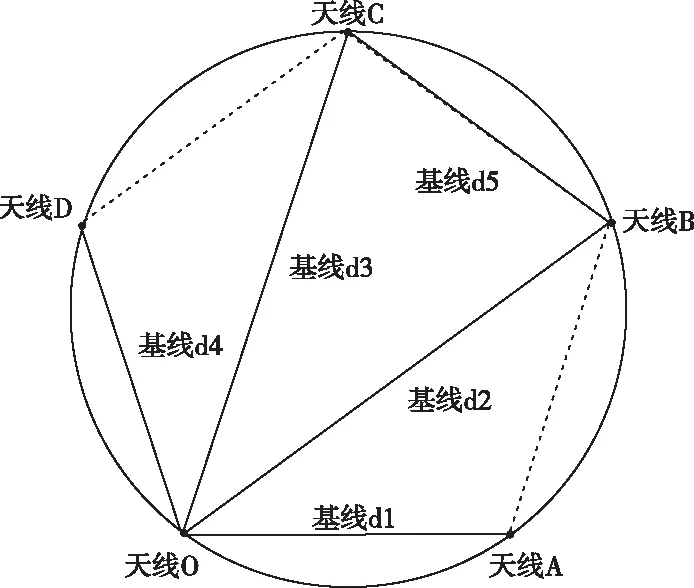
图2 天线阵元排布图
五个天线阵元(O,A,…,D)均匀排布在半径为r的圆环上,构成正五边形,共组成五条基线(d1,d2,…,d5)。来波信号从某一方向入射到天线阵列,阵列实际可测得的基线相位差分别为1、2、3、4、5,将其记为矢量形式。将与样本标准库中的数据依次进行相关匹配运算,找到与测量值最接近的样本值,该样本值所对应的方位角和仰角即为来波方向。
相关匹配过程中,用来度量数据之间相近程度的函数称为相关函数,记为J,形式如下
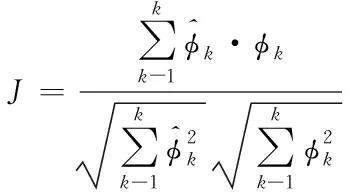
(3)
其中,φk表示样本数据的第k个值,k表示的第k个值。
2.2 无人机悬停振动对测向精度的影响
微型旋翼无人机因其体型小巧,更易受到电机转动影响产生振动,给其搭载的测向系统带来误差,因此本节首先对无人机悬停状态的振动形式进行分析,微型旋翼无人机在悬停过程中的最主要振源是作为驱动源的电机,同时气流和地面效应等因素也会对无人机产生干扰。H Schippers等学者对无人机上合成孔径雷达的振动问题做了大量实验研究,并通过实验的方式给出了无人机的一阶振动模型,本文将利用该数学模型模拟无人机的振动形式,进而分析振动对测向精度的影响。
本节中假设无人机的振动是非常理想化的单频振动[10],由强制振动激励引起的天线阵列单元位置误差Z(t)如下
Z(t)=a(t)+Z0+m1(t)Z1
(4)
其中,a(t)=ω0cos(ωt)为强制振动,ω0为振动幅度,ω为振动角频率;Z0代表弯曲模型
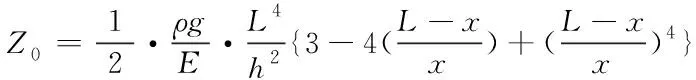
(5)
其中,L为机翼长度,h为机翼厚度,系数ρg/E=0.38×10-6;Z1代表第一振动模型
Z1=(cosh(z1)+cos(z1))(sin(z1)-sinhz(z1))
- (sinh(z1)+sin(z1))(cos(z1)-cosh(z1))
(6)
其中,z1是与材料有关的系数;m1(t)代表振动模态系数
m1(t)=Re(Q1eiωt)
(7)
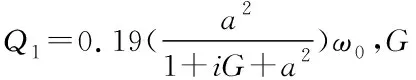
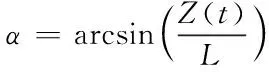
(8)
得到无人机振动所产生的姿态角变化后,本文将姿态角信息与二维相关干涉仪测向系统结合,分析振动对微型旋翼无人机测向系统精度的影响。首先在图2基础上建立右手笛卡尔直角系,Z轴垂XOY面向下,如图3所示为测向示意图,设OA基线长度为1。
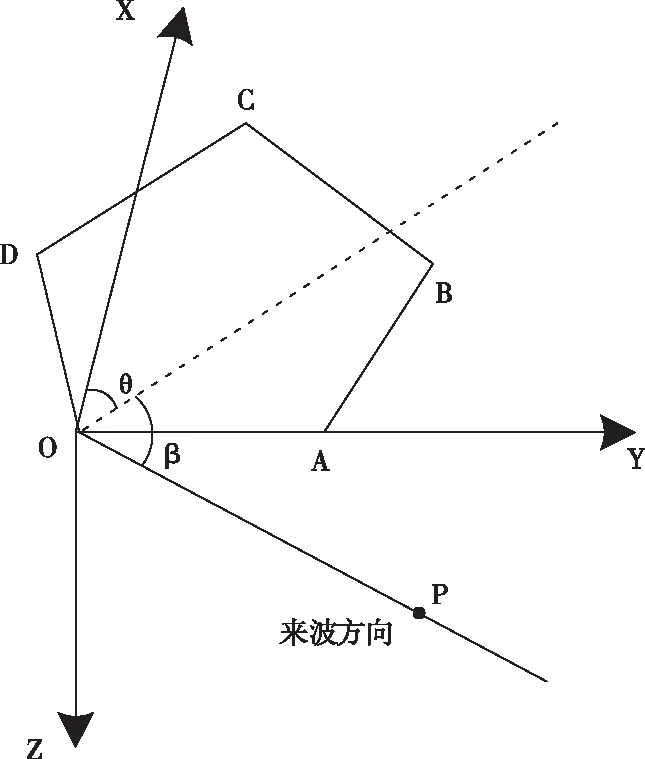
图3 测向示意图
则五基线的矢量表示形式
ΟΑ=[0,1,0]
OB=[sin 72°,1+cos 72°,0]
OC=[sin 36°+cos 18°,0.5,0]
OD=[cos 18°,-sin 18°,0]
CB=[-sin 36°,cos 36°,0]
设信号来波方向方位角为θ,仰角为β,则来波方向矢量形式为
OP=(cosβcosθ,cosβsinθ,sinβ)
(9)
设待解量为波程差Δsi,以基线d1为例进行解算,令Δs1表示基线d1的波程差
Δs1·OP(OA-Δs1·OP)=0
(10)
(Δs1)2·OP2=Δs1·OA·OP
(11)
其中OP2=1,则有
Δs1=OA·OP
(12)
推广至五条基线,令Δs=(Δs1,Δs2,…,Δs5)则有
Δs=M·OP
(13)
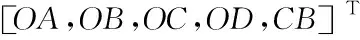
Δs=MC·OP
(14)

解算得到波程差后,通过相位差与波程差的数学关系可计算出各基线间的相位差。根据第2节所介绍的相关匹配算法,将得到的相位差与标准库进行相关匹配运算,最终得出辐射源的方位信息。由式(14)可以看出,鉴相器输出的相位差包含了因无人机振动带来的姿态误差矩阵,根据无人机一阶振动模型,振动姿态变化幅值较小,因此对测向误差近似为线性关系,且测向误差随时间的变化趋势基本与无人机振动姿态变化一致。
3 基于MIMU的振动姿态实时测量及补偿
微型旋翼无人机的悬停振动导致测向结果出现误差,解决这一问题首先要对振动姿态进行实时测量。近年来,MIMU精度和稳定性逐步提高,被广泛应用于无人机导航定位领域,其核心组件是加速度计和陀螺仪,分别用来获取加速度和角速度信息,加速度和角速度信息经连续的积分运算,最终输出载体的位置、速度、姿态等导航信息。下面将说明MIMU测量无人机振动姿态的原理。
图4为MIMU的测姿算法流程图。常用的捷联矩阵更新算法欧拉角法、方向余弦法和四元数法,其中欧拉角和方向余弦法都存在计算量大难以实现的弊端,而四元数法师利用四元数对坐标系间的旋转进行描述,具有原理简单计算量小的优点,因此,本文采用四元数法对捷联矩阵进行更新。
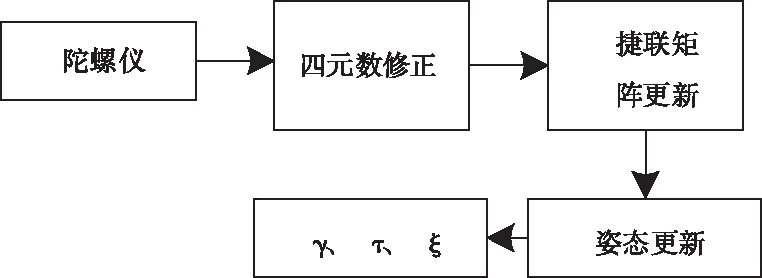
图4 MIMU测姿算法流程图
四元数的定姿公式如下
Q=q0+q1ib+q2jb+q3kb
(15)
四元数的实时更新可通过求解四元数微分方程而得到,四元数微分方程为
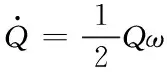
(16)
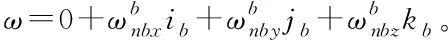
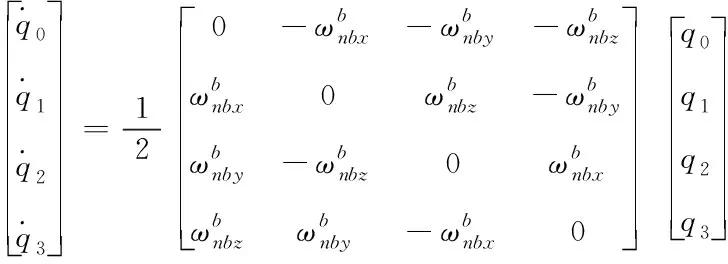
(17)
求解四元素微分方程得到q0、q1、q2、q3,根据下式可得系统的捷联矩阵
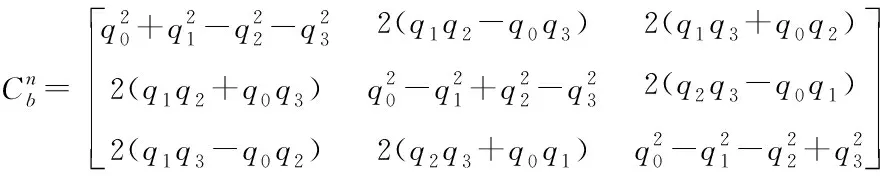
(18)
传统惯性导航系统中的捷联矩阵表示载体坐标系b相对导航坐标系n的转换关系,微型旋翼无人机振动产生是测向开始t0时刻的载体坐标系b0相对tk时刻的载体坐标系bk之间的姿态变化,因此可得到以下关系
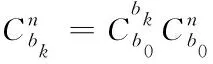
(19)
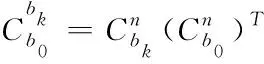
(20)
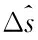
(21)
由上式可知,相位差中包含振动姿态误差,随后与样本标准库进行相关匹配运算,得出不准确的方位值[,],由此辐射源辐入射方向的矢量形式可表示为
OP=[coscos,cossin,sin]
(22)
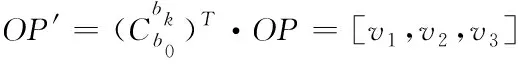
(23)
则通过式(23)进行简单解算得到校正后的方位角和仰角信息

(24)
β=arcsin(v3)
(25)
4 仿真与分析
为验证本文方法的有效性,将进行三项仿真:①微型旋翼无人机振动仿真;②振动条件下相关干涉仪测向仿真;③MIMU辅助无人机测向仿真。
实验1:根据第2.2节中给出的微型旋翼无人机振动的数学模型对其进行仿真。仿真条件见表1,无人机振动姿态变化仿真结果如图5所示。

表1 无人机振动仿真条件
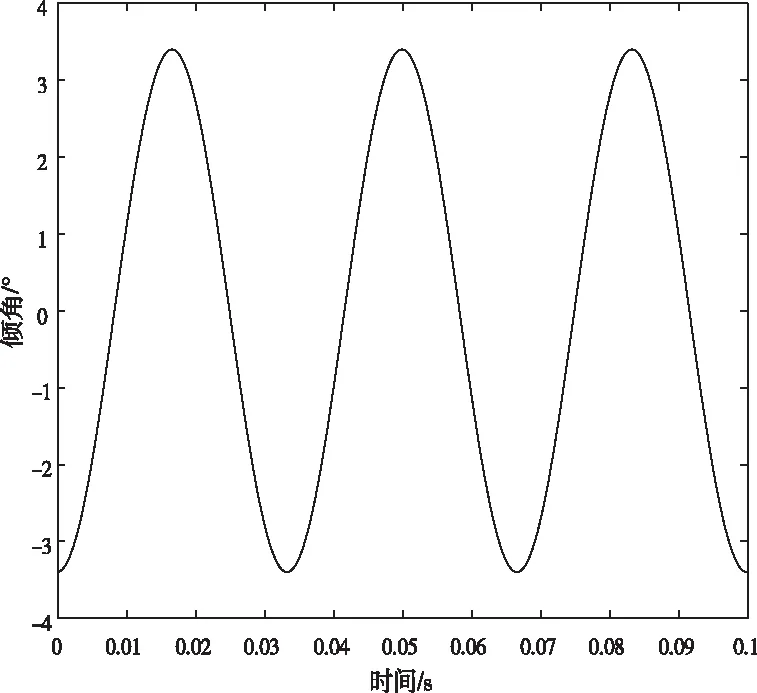
图5 无人机振动姿态变化
图5表示的是由微型旋翼无人机振动在0.1s时长内所产生的姿态角变化,可以看出微型旋翼无人机受自身电机转动的影响所产生的振动满足一阶振动模型,姿态角的变化周期与振动周期一致,其姿态角变化范围在(-3°,3°)之间,则与微型旋翼无人机固连的测向平台将具有同样的姿态变化,根据第2节中的推导可知,载体平台基准误差必然导致测向结果不准确。
实验2:根据第2.2节的推导,对振动环境下的无人机相关干涉测向系统进行仿真,分析振动对测向系统的影响。仿真条件见表2,本文以测向结果的均方根误差作为衡量标准,其定义形式如式(26)

表2 测向仿真条件
(26)
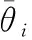
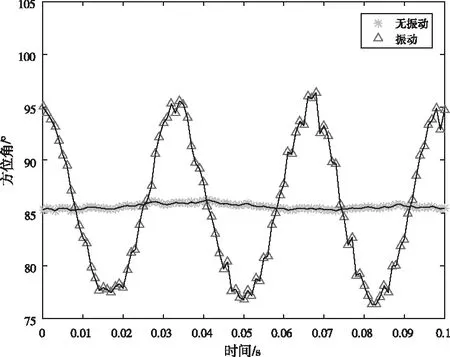
图6 有/无振动时方位角测向结果
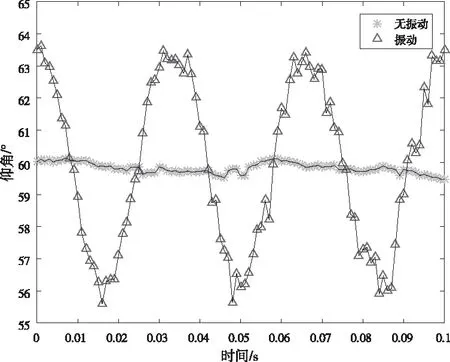
图7 有/无振动时仰角测向结果
图6、7分别表示方向角和仰角在有无振动情况下的测向结果,可以看出微型旋翼无人机测向系统存在振动时方位角测量最大误差可达到8.8°,仰角测量最大误差可达到3.2°,且测向误差的趋势与姿态变化趋势基本一致,振动所产生的姿态角越大,则测向结果偏离真实值也越大。由表3得到的REMS数值可以看出,在振动环境下,方位角的均方根误差从无振动时的0.37增至13.88,仰角的均方根误差从无振动时的0.15增至7.01,可见载体振动给测向系统带来较大误差,导致无人机测向无法完成既定任务,因此本文对测向系统的误差校正是有必要的。
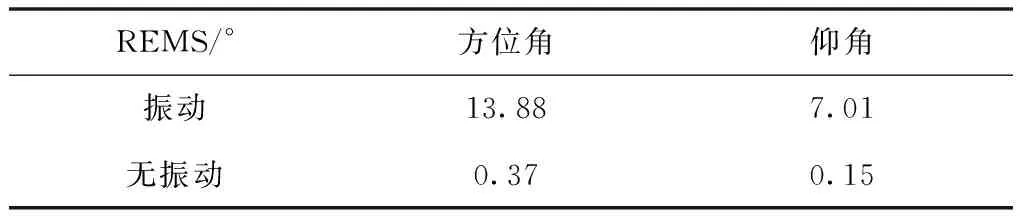
表3 有/无振动时测向RMES
实验3:最后验证基于MIMU的微型旋翼无人机测向系统的性能,根据第3节中给出的推导进行仿真,MIMU陀螺漂移0.1°/h,其它仿真条件见表2,仿真结果如图8、9所示。
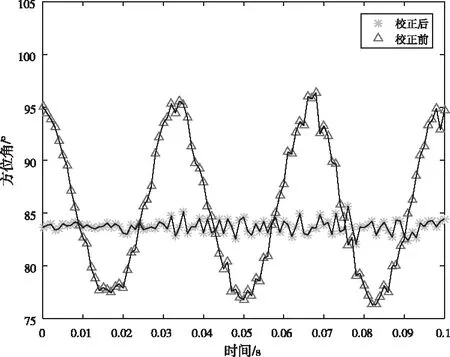
图8 校正前/后方位角测向结果
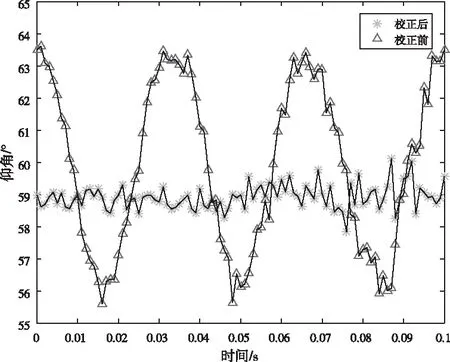
图9 校正前/后仰角测向结果
图8、9分别表示方向角和仰角在校正和未校正情况下的测向结果,由图可见校正后的测向结果比未校正的测向结果在精度上有明显提升。表4表示测向结果的均方根误差值,其中,校正后相对未校正的方位角的均方根误差减小了57.13%,仰角的均方根误差减小了54.81%。通过上述实验与分析可以看出,利用MIMU辅助无人机相关干涉测向系统后,测向精度明显提升,较好的抑制了振动给系统带来的误差,有效的提高了该系统在振动环境下的鲁棒性。
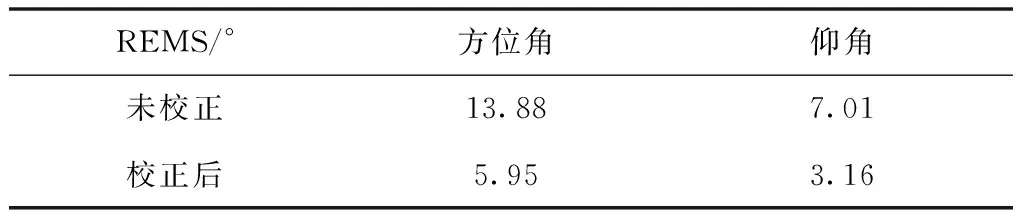
表4 校正前后测向RMES
5 结论
在微型旋翼无人机测向系统中,自身电机转动产生的振动会给测向系统带来误差,本文针对这一问题,提出了一种基于MIMU的无人机强鲁棒性测向方法。本文首先建立了相关干涉测向系统模型及无人机振动模型,并推导出振动所产生的姿态角变化,将其作为误差输入相关干涉测向系统,分析了振动对无人机测向系统的影响;然后,利用MIMU测量无人机姿态变化,通过振动姿态信息和校正算法对测向系统进行补偿;最后,利用仿真验证该方法的有效性,仿真结果表明,利用MIMU辅助的强鲁棒性微型旋翼无人机测向方法,来波信号方向角和仰角的测向误差明显降低,较好的补偿了振动所带来的测向误差,该测向方法在微型旋翼无人机测向技术中具有一定应用价值。

