基于CCA差异图融合的SAR图像变化检测算法*

曲长文，李 智，周 强，刘 晨，邓 兵

（1.海军航空大学电子信息工程系，山东 烟台 264001；2.海军航空大学科研部，山东 烟台 264001）

0 引言

合成孔径雷达（Synthetic Aperture Radar，SAR）因其具有全天时、全天候、远距离、高分辨等优点，已经成为军事、农业、海洋等领域不可或缺的侦察手段[1]。SAR 图像变化检测[2]，是对经过配准的同一地点的多时相SAR图像进行对比分析研究，目的是获取此地区在形状、位置、数量及其他属性的变化情况。

由于SAR图像受到相干斑噪声[3]的影响非常严重，光学遥感的变化检测技术直接应用于SAR图像，效果不太理想[4]。SAR图像变化检测技术发展至今，比较后分类应用最为广泛[5]。比较后分类的关键是首先构造差异图，然后再对其进行分类进而得到最终的变化检测结果。差异图的构造[6-8]方法主要有图像比值法、图像差值法，图像直接融合方法等等。后来，有学者针对各种差异图存在各自的优缺点提出了将差异图融合的方法，并且取得了不错的效果。文献[9]中提出了基于参数权重的差异图融合方法，其中心思想为对同一地点两时相的两幅SAR图像构造差值图和对数比值图，取差值图中保留细节较好的部分及对数比值图中抗噪性能较好的部分按照不同的权重参数融合，得到融合后的差异图具有两者的优点，而后再进行变化检测处理。但是文中提出的方法，参数不能自适应地选取，使得此方法操作繁琐，具有一定的局限性。文献[10]中对差异图的融合做了进一步的改进，改进后的方法利用图像中像素点的灰度统计特性自适应地选取差异图融合的权值，方法更加简单易操作，并且提高了SAR图像变化检测的精度。受上述融合思路的启发，本文提出了一种基于典型相关分析的差异图融合SAR图像变化检测方法，实验验证了融合方法简单，运行效率高，在提高变化检测精度的同时有效地抑制了斑点噪声。

1 思路框架

本文提出了一种基于典型相关分析[11]差异图融合的SAR图像变化检测方法，该方法首先用经过配准后的同一地点两时相SAR图像构造比值图、对数比值图，然后将两幅差异图经过中值滤波[12]去除部分独立像素点，之后将滤波后的比值图和对数比值图转化为列向量，将两组列向量进行线性组合，在典型相关极大的条件约束下，得到最佳的线性组合，即融合后的列向量，再将此列向量转化为原差异图大小的矩阵，即可得到融合后的差异图。对融合后的差异图应用FCM聚类[13]得到初始聚类效果图，再经过Growcut[14]算法处理得到最终的变化检测结果。本文流程图如图1所示。

图1 本文算法流程图

2 算法原理

2.1 差异图构造

假设I1和I2分别是t1和t2时刻获得的，经过辐射校正、配准后的同一区域的SAR图像，图像大小为和分别是对应图像上第i行、第j列像素的灰度值，其中，。比值图D1构造如式（1）所示，对数比值图D2构造如式（2）所示：

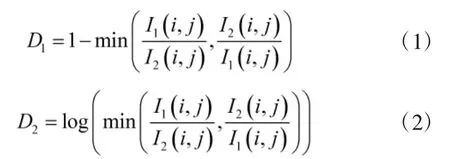
2.2 差异图融合

典型相关分析可以去除两组变量中一些必要的变量，找出具有最大相关性的变量进行融合，而通常进行变化检测的两时相SAR图像中发生变化的部分占整幅图像的比例不超过20%，也就是说差异图中的未变化部分通常占80%以上，差异图中的未变化部分具有最大的相关性。基于此本文欲使用CCA将比值图和对数比值图进行融合，融合后的图像更加突出未变化部分，取反便得到了变化的部分。下面给出比值图和对数比值图CCA融合的算法步骤。

1）将维数大小为M×N的比值图和对数比值图矩阵分别转化为大小为1×（M×N）的列向量x和y，构成原模式变换后的训练样本空间A与B；

2）计算A与B中样本的总体协方差矩阵Sxx，Syy及互协方差矩阵Sxy；

3）计算G1与G2的非零本征值以及对应的标准正交的本征矢量，其中，，，应用奇异值分解可得；

4）计算所有的典型投影矢量αi和，其中，，。取前d对投影矢量构成变换矩阵Wx与Wy；

5）利用线性变换公式抽取组合特征，即新的列向量Q；

6）将列向量Q转化为大小为M×N矩阵，即得到比值图和对数比值图融合后的差异图。

2.3 FCM聚类及Growcut分割算法

得到融合后的差异图后，对其进行FCM聚类算法处理，具体步骤为：

1）首先设置类别数、模糊度参数、容许误差；

2）从融合后的差异图中任意挑选两个像素点作为初始的聚类中心；

3）然后依次计算融合后差异图中每一个像素点到两个初始聚类中心的隶属度函数，使得目标函数最小化，得到初始变化检测结果；

4）将FCM聚类结果看作是M×N的网格，每个像素点对应于元胞自动机（Cellular Automaton，CA）中的一个细胞，根据当前的元胞状态及其邻域的状况决定下一时刻该元胞的状态，直至算法收敛，得到最终的变化检测结果。

3 实验结果与分析

为检验本文所提基于CCA典型相关分析的差异图融合的变化检测算法的可行性与适用性，并定量分析其精度，采用渥太华地区的SAR图像数据集进行验证，该数据集由在同一地点拍摄的两时相Radarsat SAR 图像组成，如图2（a）、图2（b）所示，分别拍摄于1997年5月和8月，大小均为290×350像素，图2（c）为该数据集的标准变化检测图。实验在Matlab7.1编程环境下进行。

图2 实验数据集

将数据集按照本文的算法步骤，先构造比值图、对数比值图，然后将两幅差异图进行中值滤波，再经过CCA将值滤波后的比值图与对数比值图融合得到新的差异图。实验仿真图像如下页图3所示，其中，（a）、（c）为构造比值图、对数比值图，（b）、（d）为比值图、对数比值图经过中值滤波的图像，（e）、（f）为融合差异图及其融合图直方图。最后进行FCM聚类及Growcut分割算法处理得到最终的变化检测结果，实验仿真结果与其他算法的对比效果如下页图4所示。

为定量评估变化检测的精度，同时由于Kappa系数[15]的定义中包含了更多的细节分类信息，故选用Kappa系数对其进行评价，Kappa系数定义如下：

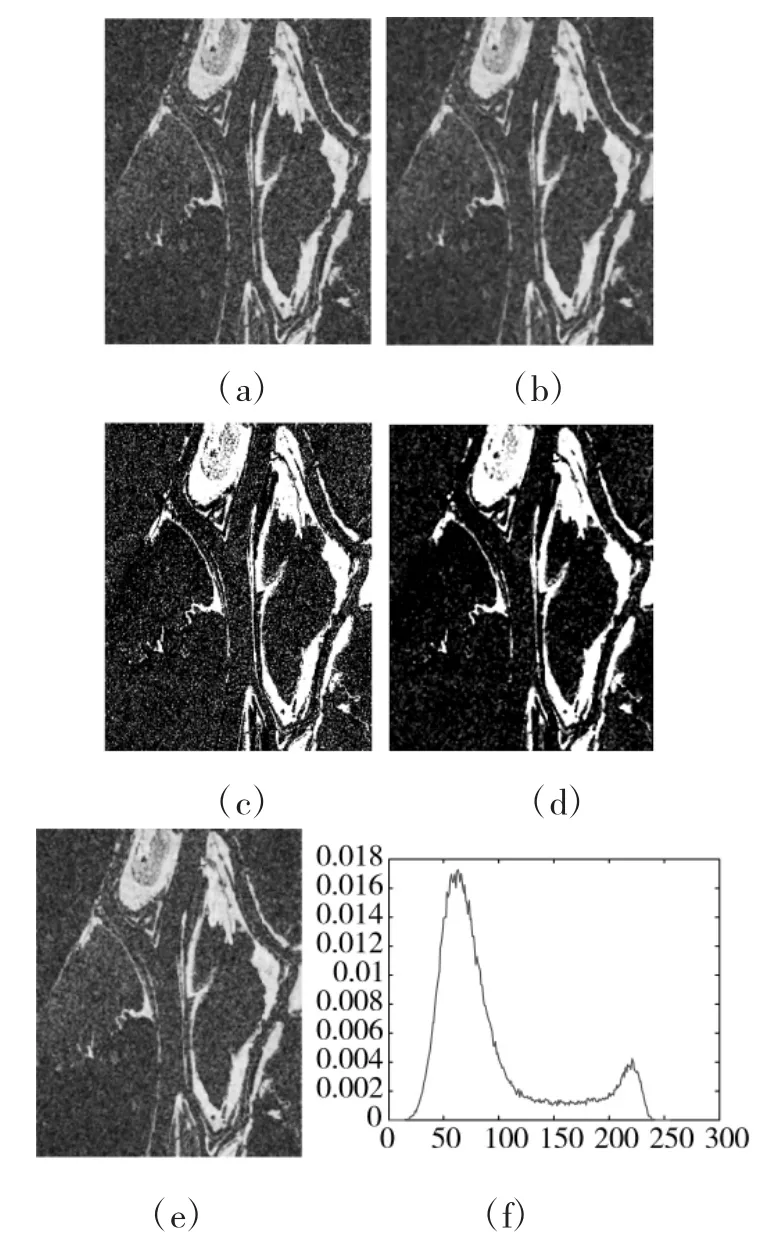
图3 差异图构造、滤波、融合图

图4 多种算法实验对比效果图

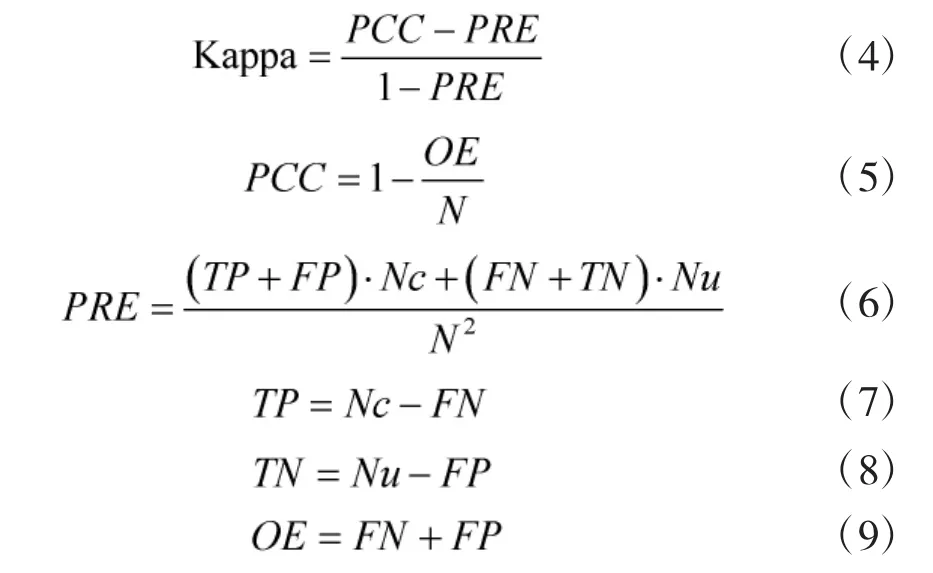
其中，FN为漏检数，FP为误检数，N为总像素数，Nc为总变化点数，Nu为总未变化点数，OE为总错误数，TP为正确检测出的变化数，TN为正确检测出的未变化点数，PCC为正确检测率。这里，Kappa系数越接近1，表明变化检测结果的精度越高，各方法变化检测精度数据如表1所示。

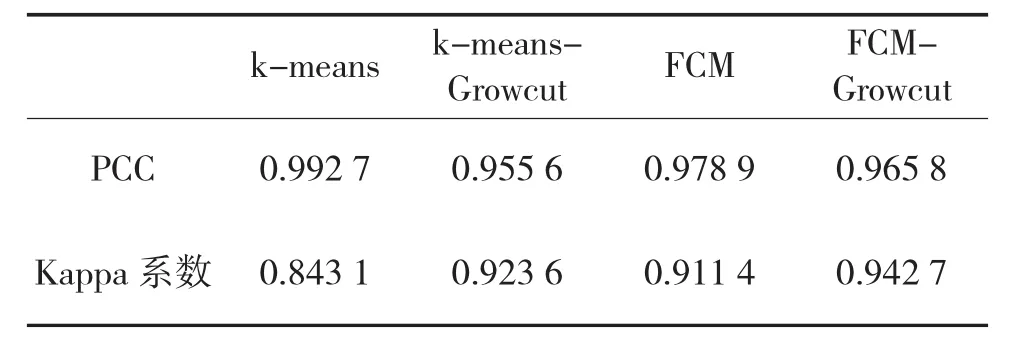
表1 各方法变化检测精度评价表

由表中数据可以得出，k-means聚类的PCC虽然最高，但是其漏检数和误检数过大，导致其Kappa系数减小。而 k-means-Growcut、FCM、FCM-Growcut在保证PCC的基础上，Kappa系数也能保持较高的水平，其中，FCM-Growcut精度评价效果最优。

4 结论

针对SAR图像差异图融合方法操作繁琐、参数不能自适应选取、计算复杂这一问题，本文提出了基于典型相关分析（CCA）差异图融合的SAR图像变化检测算法。该算法首先构造比值图、对数比值图，然后经过中值滤波，将滤波后的比值图和对数比值图转化为列向量并将两组列向量进行线性组合，在典型相关极大的条件约束下，得到最佳的线性组合，即融合后的列向量，再将此列向量转化为原差异图大小的矩阵，即可得到融合后的差异图。对融合后的差异图应用FCM聚类得到聚类效果图，而后对聚类效果图应用Growcut分割算法处理得到最终的变化检测结果。实验采用渥太华地区的SAR图像数据集进行验证，由实验仿真结果可以得出本文所提基于CCA差异图融合的SAR图像变化检测算法，具有很高的变化检测精度，是适用可行的。下一步研究的方向是从差值图、比值图、对数比值图、模糊相似度贴近图、杂波分布比值图、似然比图等各类差异图中寻找合适的差异图进行两两融合，经过FCM聚类及Growcut分割算法处理，以期获得更高的变化检测精度。