一类杀虫剂具有残留和滞后效应的害虫治理模型的研究
赵美华,刘 兵,刘海波,胡 雪
(1.辽宁师范大学 数学学院,辽宁 大连 116029;2.鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007)
随着农业经济的发展,人们越来越关注害虫种群的控制问题.喷洒化学杀虫剂和投放天敌是比较常用的两种方法.文献[1-6]假设杀虫剂是瞬时成比例杀死害虫的,考虑到害虫对杀虫剂的抗性发展,文献[6]建立了周期轮换使用杀虫剂并考虑不同时刻脉冲作用下的害虫综合治理模型.文献[7-8]在抗性基础上引入杀虫剂作用函数,但只考虑到杀虫剂对害虫具有残留效应.由于许多杀虫剂对害虫具有残留作用的同时往往还有一定的滞后效应[9],喷洒杀虫剂之后,一旦这种滞后效应发生,害虫种群密度不会立刻下降,反而会继续保持原有的上升趋势,直到滞后效应消失,害虫种群密度才会下降,并且这种滞后效应一般会使害虫种群密度超过经济临界值[10].因此,在害虫化学控制中,有必要把这种滞后效应考虑进去.本文引入杀虫剂作用函数,考虑到杀虫剂的残留和滞后效应,建立了一类具有抗性发展的害虫治理模型,分析了害虫灭绝临界条件,给出了杀虫剂的切换策略,所得出的结论为相关问题的实际操作提供了理论依据,具有现实的生物意义.
1 模型建立
考虑到杀虫剂的残留和滞后效应,本文假设周期喷洒杀虫剂,设周期为T,采用文献[9]中的b(t)函数:
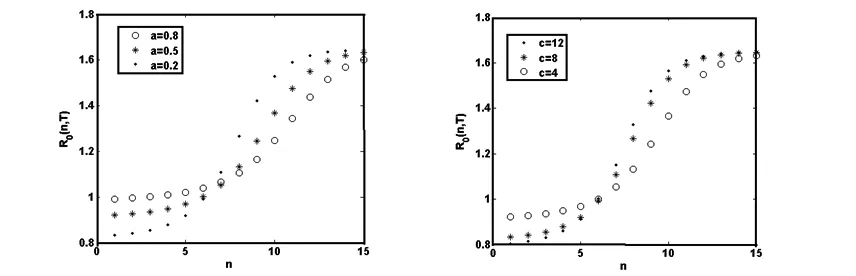
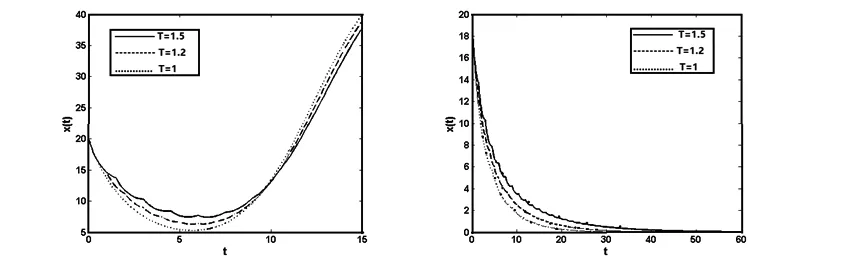
b(t)=m[e-a(t-nT)-e-c(t-nT)],nT (1) 其中,m是杀虫剂对害虫的有效杀死率,满足m=1-e-kD或m=e-kD,k是正常数,D是杀虫剂剂量;a是杀虫剂对害虫的衰减率,c是杀虫剂对害虫的滞后效应率,且满足c>a. 假设害虫种群的自然增长满足Logistic方程,即 (2) 本文将害虫种群分成易感害虫xS(t)与抗性害虫xr(t)两种,其中,易感害虫是指没有对杀虫剂产生抗药性的害虫,设其在t时刻所占比例为q(t);抗性害虫是指对杀虫剂产生抗性的害虫,t时刻所占比例为1-q(t),则xs(t)=q(t)x(t),xr(t)=(1-q(t))x(t).因此,易感害虫xS(t)与抗性害虫xr(t)满足如下方程: (3) 害虫的种群增长模型变为 则系统(3)可变为 (4) 其中,x(0)=x0,q(0)=q0,x0代表初始时刻害虫种群密度,q0代表初始时刻易感害虫所占比例.通过计算,系统(4)在任意区间nT (5) 为了说明杀虫剂残留和滞后效应对害虫抗药性发展的影响,图1分别取a=0.2,a=0.5,a=0.8,其它各项参数取值为T=1.5,q0=0.99,c=8,m=0.8.模拟出q(t)随时间的变化趋势,可以看出衰减率a越小抗性发展越快,也就是杀虫剂的残留越大抗性发展越快;图2分别取c=1,c=3,c=10,其它各项参数取值为T=1.5,m=0.8,q0=0.99,a=0.4,m=0.8.模拟出q(t)随时间的变化趋势,可以看出滞后效应率c越大抗性发展越快. 对于非自治系统 (6) 引理1假设系统(6)满足 (3)∃β>0, (i)当t≥0时,F(t,0)β; 系统(6)以x(0)=x0为初值的解满足当t→时,x(t)→0. 图1 杀虫剂的残留效应对易感害虫比例q(t)发展影响图 图2 杀虫剂的滞后效应对易感害虫比例q(t)发展影响图 定理1如果R0(n,T)<1,n∈N时,则系统(5)满足以x(0)=x0>0为初值条件的解x(t),当t→时x(t)→0.其中, 证明系统(5)中,F(t,x(t))=r(1-ηx(t))-b(t)q(t),显然引理1的条件(1)成立. F(s,0)=r-m(e-a(t-nT)-e-c(t-nT))q(t)r,所以条件(3)中(i)成立. 由引理1的条件(3)中(ii)知,如果R0(n,T)<1,那么系统(4)满足以x(0)=x0>0为初始条件的解x(t),当t→时,x(t)→0.证毕. 根据R0(n,T)的表达式可知,R0(n,T)是关于n的单调增函数.图3是在改变a的情况下R0(n,T)随着喷洒次数变化的趋势图,图3中显示杀虫剂对害虫的衰减率a越大,害虫根除临界值越大,害虫种群越容易爆发.图4是在改变c的情况下R0(n,T)随着喷洒次数变化的趋势图,图4中显示杀虫剂对害虫的滞后效应率c越小,害虫根除临界值越大,害虫种群越容易爆发,其中,基本参数取值为T=1,r=0.5,η=0.01,m=0.9,a=0.2,c=8,q0=0.99.图5模拟的是不同喷洒杀虫剂周期下害虫种群变化趋势,其中,基本参数取值为r=0.5,η=0.01,m=0.9,a=0.2,c=8,q0=0.99.由图5可以看出在喷洒杀虫剂初期,害虫种群整体趋于下降趋势,但随着害虫抗药性的发展,害虫种群下降到一定程度后会逐步增加,最终会持续生存.为了控制害虫种群,本文接下来给出了两种切换杀虫剂的策略. 图3 杀虫剂对害虫的衰减率a对临界值R0(n,T)影响图 图4 杀虫剂对害虫的滞后效应率c对临界值R0(n,T)影响图 方法1以临界值R0(n,T)为杀虫剂切换依据: (7) 其中,[]表示取整函数. 图6中曲线上的黑点表示杀虫剂的切换时间,由图6可知,当T=1时,每隔4次切换另一种杀虫剂;当T=1.2时,每隔2次切换杀虫剂;当T=1.5时,每隔1次切换杀虫剂.应用这样的策略切换杀虫剂害虫种群最终会得到控制,其中,基本参数取值为r=0.5,η=0.01,m=0.9,a=0.2,c=8,q0=0.99. 图5 不切换杀虫剂的情况下x(t)随时间变化趋势图 图6 以临界值为切换依据害虫种群的变化趋势图 方法2以杀虫剂效率为切换依据: 对于固定的周期T,用x(nT)表示在nT时刻害虫种群数量,由于x(nT)不是单调数列,则存在一个n1∈N,使得 x(T)>x(2T)>…>x((n1-1)T),x((n1-1)T) 其中,x(nT)满足如下迭代公式: 对于固定的n,由函数f(n)可以确定一个自治差分方程,即 对此,我们作出如下讨论: 综上可知: 这里a(n-1)=R0(n-1,T)>1.因此 (8) 本文考虑到杀虫剂对害虫具有残留和滞后效应,建立了一类杀虫剂作用函数与害虫抗药性相结合的害虫治理模型.研究了害虫根除临界条件,可以看出杀虫剂对害虫的残留和滞后效应都会对害虫抗药性发展产生影响,且随着害虫抗药性发展,害虫最终会爆发.本文以临界值和杀虫剂效率为依据给出了两种杀虫剂的切换策略.在以后的研究中,我们会采用化学控制与生物控制相结合的方法来进一步延缓害虫抗药性发展,最终进一步控制害虫数量.
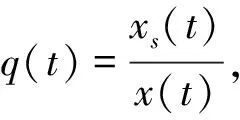
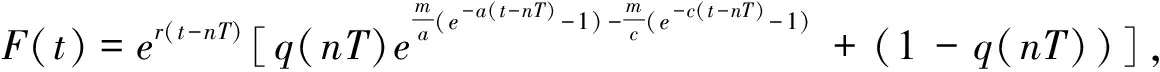
2 害虫灭绝临界条件
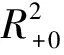
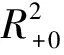
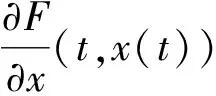

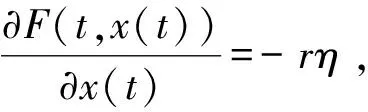

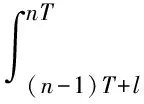
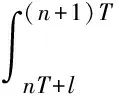
3 杀虫剂切换策略




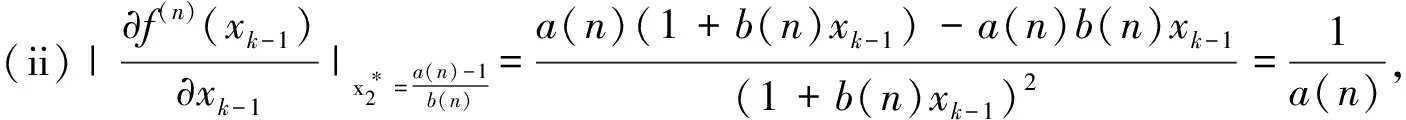
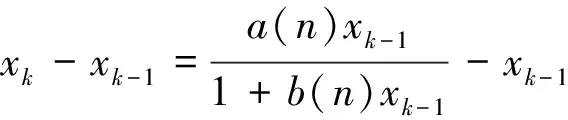
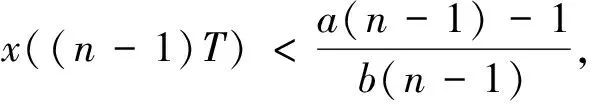
4 结论

