基于经验 相机而教
——以“角的度量”教学为例
□胡冬梅
“角的度量”是人教版四年级上册的内容,“认识量角器,并能正确使用量角器量角”这两点是本课的教学重点与难点。我们在教学中发现,此类课总会出现“上课会量,下课即忘,一操作就错”的现象,那么,技能的教学到底怎么教?
【教学前测】
带着这些问题,我首先对我班的学生进行了知识前测。
1.(出示量角器)你知道这个学具叫什么吗?量角器是用来做什么的?
2.量角器上有角吗?请指出来。
3.请试用量角器量出已知角。

结果发现学生都认识量角器并能叫出其名,知道它是用来量角的大小,但学生在找角时却错误百出(如图1、图2),更无法正确量角(图3、图4)。

图1

图2

图3

图4
进一步对这些学生进行访谈,他们满脸困惑。
生:量角器的形状与角的形状不一样,角是尖的,两条边是直直的,而量角器有那么多线,没有“尖”角,一条边还是曲的,“曲的”怎么能量“直的”呢?

【教学过程】
针对此种情况,如何基于学生的经验,既激活学生潜在的知识,又能体现量角工具和量角方法的与众不同,达到突出重点突破难点之效?笔者对此课教学作了精心的设计。
一、课前
提供一些学具,让学生量一量身边物体的长度,而后让他们回忆体会量的过程中,用什么工具量线段或面积的大小和量的方法,小结得出度量的基本方法:用已知量去度量未知量。从而抓住方法的核心,为本节课度量角的大小做好铺垫,降低难度。
二、基于内需的导入
三个小朋友丁丁、当当、铃铃在一起玩波波球“滑滑梯”游戏比赛,看看谁的波波球滑得最快。我们一起去看看。
课件显示:通过抽签选斜板,丁丁的波波球直接从接近直角的斜板上滚下来;当当的波波球在呈45度角的斜板上滚下来;铃铃的波波球在呈15度角的斜板上滚下来。结果出来后引起一番争执。
丁丁:哈哈,我赢啦!
铃铃:这不公平,你的斜板太“陡”,一下就滑下来了,我的斜板“不够陡”,当然滚不过你的球。
当当:我的既不是最陡的也不是最平的,所以只能得第二。
师:咦,你能解释一下“陡”和“不够陡”的意思吗?
生1边比画边说:“陡”就是“斜”的意思,有些斜板太“斜”了,有些只是有点“斜”。
生2:太“斜”的那个角很大,平的角就很小。
师:嗯,你提出了一个很有价值的问题,就是“角“有大小之别,那角的大小用什么来度量?这节课,我们一起来学习角的度量。板书课题:角的度量
三、以直角为标准角,降低学习难度
从调研可知,量角器的半圆形状给第一次使用量角器的学生带来了很大的困难。为了突破这一难点,我们设计了让学生体验自制量角工具的过程。
师:谁告诉我,第一只猴子容易摔跤的滑梯与地面形成什么角?
生:直角。
师:你怎么肯定是直角呢?
生:我可以用三角尺量一下。
师:但我手中只有一个正方形,你能准确告诉我这个角是不是直角吗?
教师引导学生用正方形的一个直角与斜板所形成的角进行边边重合,比较后得知,这是一个直角。并指出:直角是90度,“度”是角的计量单位,可以用符号“°”表示,写在数字的右上方。(板书课题:角的度量 角的计量单位:度“°”,并引导学生书空:90°)
师:要想知道第二个角多大,用我这个正方形的角还能测量吗?
学生上台操作发现正方形的直角测量不了(锐角):这是直角,但量的是锐角,量不了。
师:好,没有锐角,我们能利用正方形的直角变成一个锐角吗?
生:可以用折一折的方法。
教师引导学生边操作边验证,发现所量锐角与把直角“两等分”时的角一样大,这个角就是直角的一半,也就是45°角,用这折成的角进行测量,第二个滑梯与地面形成的角刚好重合。
师:通过你们的操作,测量出第二个斜板与地面形成的角有多大?是怎样测量出来的?
生:测出来了,是45°角,我们把大角通过折一折变成小角,对折一次刚好一样大。
有了第二个角的测量经验,对于第三个角,学生想到把45°的角再折小点,经过几番尝试,发现把45°角进行三等分,每个角为15°,再用自制的量角工具进行第三次量角,得出待测角与正方形里的15°角的两边刚好重合,是15°。
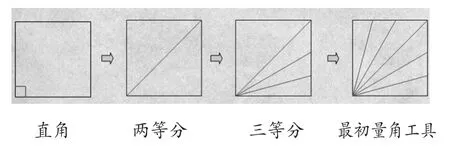
用学生经验中很熟悉的“直角”作为最初标准角,从直角的两等分到三等分的过程,形成最初的45度角、15度角的量角工具,初步体会量角工具的制造过程,就是把大角不断细分成小角,总有一个小角适合已知角,为后续完善量角工具做好铺垫,起到承前启后的作用;而且通过三次操作有了最基本最重要的量角方法:把已知角与待测角的两边重合、点点重合,初步渗透量角的要素,降低了量角的难度。
四、在改造量角工具的过程中掌握角的度量方法
有了初始的量角工具,笔者继续提出量更小角的要求(如5度、3度、2度)。
师:如果这时我要量这些角,还能用刚才的量角工具吗?
生:不能,还要继续折小一点的角。
于是学生不断把原有的角进行两等分、三等分,直到细分到1度,至此已把一个直角平均分成90份,其中一份就是1°。
另一方面,为量更大的角度,如110度角,教师引导学生在另一边重新拼一个直角,以同样的等分方法进行均分。
师:为更方便地使用工具,有必要对量角工具进行适当改造。如:标上刻度,把刻度线统一长度,去除边角和太过密的射线。

【评析】通过师生一起努力,与量角器形状相同的半圆形,即量角器的雏形出现了。由于亲自设计并创造出量角工具,学生对那些角和边的由来有了清晰的认识,他们可轻松找到量角器的中心点、刻度线、标准角,不再对角“视而不见”。
五、体会量角工具的局限性,完善工具并学会灵活度量角的大小
受思维定势的影响,学生对开口向右的角最乐于接受,但对于开口向左的角却不习惯,为克服思维的刻板性,接下来教师设计了变式练习。

对于开口向左的角,教师先让学生猜一猜这个角可能会是多少度,学生纷纷猜测大约是25度、30度、31度……在此基础上让学生用量角器量。有的学生顺利摆好量角工具后,读出150°,此结果与学生的猜想相去甚远,引发学生的疑惑。
生:这么小的角不可能是150度吧,但量角器上明明显示的是150度啊。
经过研究,学生发现了问题所在:这150度不是我们要量的角的度数,应该用180度减去150度等于30度才是正确答案。因为角的两条边夹住的角才是我们要量的,而150度量出界了。
商量解决办法,最后得出:为了更方便地量开口向左的角,可在原有工具中再添一圈角度,这样,量角工具便有了内外两圈角度,可以更方便量出开口向左或向右的角的大小。至此,一个现代量角器顺利诞生,此时,组织学生观察、讨论如何用量角器量角,总结出量角四要素:点对中心点,边对“0线边”,看清内外圈,再看另一边。

六、熟练使用量角器,正确量各种角
(一)再量特殊角
再次量特殊角:课件出示各种开口的角。让学生先猜猜其大小,而后充分讨论,操作交流,得出此类特殊角的量法与向左向右角的量法本质是一致的,都是点对中心点,边对“0线边”,看清内外圈,再看另一边。不同的是量角器的摆放位置。

(二)猜一猜

笔者让学生在猜测与实证过程中进一步掌握正确的量角方法。
从制作最初始的量角器到尝试度量角的大小碰到量角的不方便,基于量角的需求,到最后完整量角器的诞生,学生一直在探索,这样的学习充分激活了学生自主学习的主动性,在不断的创造过程中不但体会到一种新的度量工具产生的全过程,还在矛盾冲突中学会了灵活量角的方法。
七、拓展深化,让学生的思维走得更远
课件显示,两条鳄鱼比嘴大小。从而得出:角的大小与其两条边的长短无关。
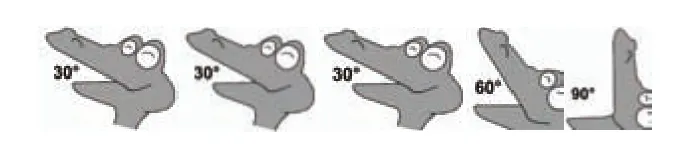
课件继续显示,鳄鱼张嘴吃肉的情景。从而得出:角的大小与其张开的幅度大小有关。
这一环节,由学生喜闻乐见的鳄鱼吃肉情境引入,两条鳄鱼比嘴大小,同样的一条鳄鱼嘴张开的角度随其张开的大小而变化,直观呈现和感受角的大小与其两边长短无关,而与其张开的程度有关。
八、想开去,让课堂焕发持久魅力
师:想一想,本节课我们学会了什么?说说你的收获。
师:如果我要量一个190度的角,是否有特别的量角器呢?

课件出示生活中各种量角器。

师:为了量各种各样的角,就有了各种各样的量角器,如全角量角器、电子量角器、万能量角器等。
师:生活中还有另外的一种角,这些角度又该如何度量呢?请同学们课后去查找研究,下节课我们继续交流探讨。
课的最后,介绍了各种量角工具,甚至是有别于量角工具但又与角有关的经纬度,意在给学生开拓眼界,进一步激发学生的学习兴趣。
在课堂中,教师如何基于学生的活动经验进行教学,让教有方向,学有所得?本课中教师针对以往教学中遇到的问题,进行课前调研,以此为依据设计整个教学流程;以生为本,自制量角工具,体会量角器产生的过程,在此基础上整体构架,集认识量角器与用量角器正确量角于一体。整节课没有一处提到数学思想,但却处处蕴含数学思想,如刻度与角度一一对应的思想,量角工具诞生过程的模型思想,分角过程的极限思想等。整个教学过程环环相扣,步步深入,以“课前调研法”为统领,精心铺排:情境教学—合作交流,启发引导—讨论猜想,抛砖引玉—自主建构,经历全程—操作验证。这些教法与学法结合一系列有针对性和层次性的课前教学准备,让学生享受到探索知识的惊喜,欣赏到知识呈现的美丽!
——以“画角的复习”教学为例

