让学生在发现、研究、探索中成长
——数学实验课实践例谈
□ 邢佳立
自2001年新课程改革以来,学校教学的范式已经从以往以教师为中心的教学模式,逐步转换成以学生为中心的模式。教师在课堂教学中的角色更多的是引领者、促进者和协助者,课堂学习的主体聚焦在学生。苏霍姆林斯基说过:人的内心里有一种根深蒂固的需要——总想感到自己是发现者、研究者、探索者。在儿童的世界中,这种需要特别强烈。但如果不向这种需要提供养料,即不积极接触事实和现象,缺乏认识的乐趣,这种需求就会逐渐消失,求知兴趣也与之一道熄灭。[1]如何在数学课堂教学中,体现以学生为中心,让学生感受和成为学习的主人,需要数学教师有针对性地做好课程设计。数学实验课因其活动“具有具身认知特点”“材料往往是生成性资源”“任务引人入胜”等特点,可以更好地满足学生以上心理需求,又有利于帮助学生发展那些难以清晰表达的,如数学信念、经验、思维、直觉、灵感等“隐性知识”。
本文以几节数学实验课为例,试对数学实验的设计提出思考。
一、设计让学生有所“发现”的实验课
【案例一】
学生在学习数学的过程中,总有一些共性的“难点”“瓶颈”难以突破,比如学习“三角形面积”时,需要学生能将三角形转化为已经学过的图形,用已学过的面积计算方法来解决三角形的面积问题。如果没有教师的引导与介入,学生很难自觉想到用两个同样的三角形拼成一个平行四边形(倍拼)的方法。倍拼的方法并非在学习三角形时才出现,学生之所以迁移的能力不足,与他们缺少“倍拼”的基本活动经验有很大关系。是否有可能设计一节数学实验课,让学生自然而然地发现“倍拼”是帮助解决图形问题的重要方法,从而帮助学生积累这种经验,促进学生有关图形知识的内化与迁移。
带着这样的思考,我们设计了“钉子板上围图形”[2]一课。整节课的教学环节大致如下。
(1)介绍学习工具:钉子板与橡皮筋。钉子板上最靠近的4个“钉”中间的部分,我们称之为“1格”,用橡皮筋在钉子板上可以围出各种图形。它们围出的格子数可以不一样。
(2)呈现已学图形:在钉子板上呈现围好的长方形、正方形、梯形等图形,请学生数一数,各占多少格。

(3)引导猜测与画图:如果在钉子板上围“占2格”的图形,可以围出多少个?并把自己想到的画在方格纸上。
(4)实验操作与交流:围占2格的图形,先在钉子板上围图形,并把围出的图形画下来,再和同伴说一说,这些图形是占2格吗?如何说明?
(5)实验延伸与拓展:围占3格的图形,可以围多少个?你是怎么想的?
在这一案例中,学生最初猜测“钉子板上围占2格的图形,可以围多少个”的时候,多数学生认为可以围2~3种,猜可以围4种或4种以上的学生不足20%。学生最初围出的图形大致如图1所示。

图1
但在相互交流中,学生发现,可以根据格子的累加来“设计”图形,1格+1格,只有长方形,1格+半格+半格,就可以有多种方式了,除了直角三角形、平行四边形、梯形以外,还可以拼成不规则图形(如图2);如果是半格+半格+半格+半格,那么又可以拼成不同的图形(如图3)。

图2

图3
接着,有学生围出图4,这也占2格吗?怎么说明它也占2格?学生自然地采用了图5的方式说明:原来,4格的一半也是2格(倍拼的方法如期而至)!
至此为止,课堂上,学生就像打开了潘多拉魔盒一样兴奋起来,“我发现:3格的一半是1格半,再加上半格也是2格!(如图6)”“5格的一半是2格半,去掉半格也是2格!(如图7)”甚至有学生提出:要是钉子板再长些,这样也可以,这是8格的一半4格,去掉4格的一半是2格(如图8)……
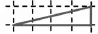
图4

图5
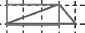
图6

图7

图8
在这个过程中,图形的割补、倍拼,学生都在体验,图形面积的可加性、面积的不变性学生都在感受,甚至“同底等高的三角形面积相同”学生也在操作、实验中有了直观的知觉经验。
我们对上过这节课的6个班级237名学生,在学习“三角形面积”一课之前,做了前测调查,结果显示有146人能独立想到“倍拼”这一方法,占总人数的61.6%。在学习了基本图形面积以后,有80%以上的学生可以独立解决稍复杂的“组合图形面积”问题。虽没有直接证据证明这是本节实验课的“功劳”,但我们依旧相信,这节课帮助学生积累的活动经验,形成了我们看不见的“隐性知识”,正是这些隐性知识,助力学生的后续学习。这节实验课让我们看到:只要操作的材料合适,问题合适,学生自己的“发现”,在学生的隐性知识学习中有强大的作用。
二、设计让学生不断“研究”的实验课
【案例二】
“空间观念”如何培养一直是一线教师教学时一个“模糊”的点。以人教版教材五下中的“观察物体”为例。
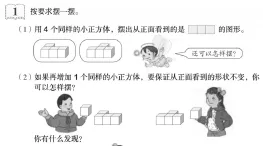

教学该课时教师经常感到,这是一节很“无用”的课,不是教学内容的无用,而是教学本身经常是“隔空打牛”“隔靴搔痒”,起不到真正的作用。稍复杂一点的图形,对于“会”的学生来说,即使这节课不上,相关内容学生也可以解决;对于“不会”的学生来说,即使上过了这节课,让其自己思考,依旧无从下手。为什么会这样?“观察物体”为什么这么“难教”?
从心理学的视角看,与空间观念有着密切联系的概念有空间知觉、空间表象、空间想象和空间能力。“观察物体”需要学生在头脑中对原有的“表象”进行加工,融入一部分“空间想象”解决眼前的问题。通过调研发现,“观察物体”让学生感到困难的主要原因是:学生缺少空间知觉的支撑,难以形成空间表象,没有表象自然无从想象,而“当空间想象受阻时,提供操作材料动手实验,是行之有效的教学对策”[3]。培养空间能力的一个重要条件就是让学生看到、接触到学习的对象。那么是否可以设计一节实验课,以丰富学生的空间知觉为目标,从而促进学生空间能力的发展呢?
小学生形成、发展空间观念主要依靠“视”与“触”,亦即主要途径、手段是观察与操作[4]。因此我们设计了数学实验课“图形穿越”[5],为学生提供我们自己设计的可以相互“黏”在一起的立方体(罗永军,专利号:CN205461022V),以及可以当作“墙”的卡纸作为教具,创设立方体可以“穿墙而过”的情境,引导学生在“抓盗贼”的任务驱动下,不断地通过拼搭、观察、思考、想象、操作与反思等活动,丰富学生对小立方体搭成立体图形的“知觉”。同时,我们将立体图形与其三视图对应关系,与学生实际生活的房间中物体从不同方向“穿墙而过”留下的痕迹联系起来,触觉、运动觉与视觉的协同活动成为学生获得空间表象的有力支撑;让学生能够在丰富的对小立方体的知觉前提下,形成立体图形与其三视图的表象。

(磁力立方体)

(穿“墙”卡纸)

(穿墙而过)

(房间里的立体图形)
实践表明:这节课除了非常受学生的欢迎,让学生欲罢不能以外,学生在课前与课后解决相应问题的正确率有大幅度提高,理论和实践都告诉我们,这样的实验课的确对促进学生的空间观念发展有作用。
三、设计让学生充分“探索”的实验课
【案例三】
培养学生创造性思维是数学教育的重要目标之一,但学校数学教学中,数学表达的统一性、简洁性,数学题解法和答案的唯一性,往往又制约着学生“创新思维”的形成。对“探索”过程的经历,能够激发学生正向的学习情感,能够培养学生的积极数学精神,已经是大家的共识。课堂上,教师也注意到了要让学生经历“探索”的过程,但由于课堂时间、教学任务和教学内容所限,课堂上的探究往往成了“走过场”式的假探究。是否可以适当地将教学内容设计成实验课,真正让学生经历“探索”答案的过程,以增加学生与“创造性思维”相关的隐性知识呢?
罗永军老师设计的“掷骰子”[6]一课,就源于此初衷。
“骰子”有6个面,相对面点数的和为7,如果将一摞骰子摆起来,只看到最上面的骰子朝上一面的点数就可以知道这一摞骰子“看不见”的所有面的点数之和(若有a颗骰子,最上面一粒骰子朝上的点数为b,则“看不见”的点数之和为
n=7a-b)。知道这个规律、解决相应的问题远不是这节课的目的,而这样的规律,学生自己是不是可以发现?他们是怎么发现和解决问题的?
教学时,罗老师先请学生看了一段视频,一名可以猜到答案的男生声称自己有“透视眼”,所以可以“看到”大家看不见的面上的点数。这当然引起了学生们的兴趣。罗老师问:“这个透视眼是天生的还是可以练出来的?”“咱们也练练,看是不是可以练出来。”从一颗骰子开始“练”起。课堂上一个调皮的学生学着“拜菩萨”的样子,嘴里喊着“3、3、3……”骰子一扔,不是3,沮丧地再来一次,“3、3、3……”哇,居然真是3,看他喊“我练成了!”的样子,真让人忍俊不禁。当他看到同伴通过反复观察,发现只要朝上的一面是1,看不见的就是6……这样的规律,从而“练成”看一颗骰子的透视眼时,惊讶地发现数学原来比“菩萨”好用多了,进而在与同伴交流的基础上,总结出一颗骰子的“透视眼”是“只要用7减去对面的点子数会算,就练成了”的结论。

实践中,我们还惊奇地发现:即便学生已经知道“相对面的点数和是7”,到发现“有几颗,看不见的点子数就是几个7减去最上面的数”还是要经历一段“曲折”的探索过程,而不是像我们想的那样“很快”就能迁移过来了。这节课教学内容简单,如果学生已经知道这个规律,解决问题无非就是“套用公式”,但是对“什么是教学”的思考,以及教学法的转变让我们感受到:如果给学生足够的时间,让学生在感到足够安全的基础上探索,这样的实验课很有价值!
杜威认为:“一切教育活动的首要根基在于儿童本能的、冲动的态度和活动。”[7]但如果“实验”仅仅等同于“活动”,显然缺少了数学教育的价值。回顾以上几个教学案例,可以看到,我们设计的每一节数学实验课,都是带着对数学问题的思考,带着对学生学习中遇到的问题与他们对困难的理解而设计。我们理解的数学实验,数学是核心内容,促进学生隐性知识的积累是目的,实验是教学方式。虽然教学环境下的实验,不那么精准,但它却极具生态性,让隐性知识的教学变得可操作、可把握。希望数学实验课能够带领学生在“发现”“研究”“探索”中不断成长。

