学生“数线上标小数”能力的后测与分析

□ 陈小霞

在小学数学教学中，教师通常会通过许多表征方式进行教学活动。数线作为学习“数”的重要材料，经常出现在学习整数、分数以及小数等内容中。在三年级下册“小数的初步认识”的学习中，教材大量运用了数线这一表征方式帮助学生理解小数的意义，在教材配套的练习册中也经常出现有关数线的练习。学生在三下已经学过“小数的初步认识”，经历过期末复习和期末检测的学生，那么他们对“数线上标小数”这一知识点的理解达到了什么程度？为了解学生的真实掌握情况，笔者设计了相应的后测题，对学生进行了测查。

一、后测题

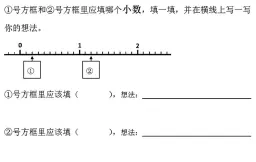
二、测查的对象及过程

笔者选择两个班级的学生作为样本，共计60人。这些学生在三年级下册的最后一个单元学习了“分数的初步认识”和“小数的初步认识”，并且已经完成了期末复习和期末检测。学生在期末试卷上考到了“数线上标小数”的问题，但在测查前教师并没有对期末试卷上的相关问题进行讲解。教师以班级为单位测试上面的题目，不提供任何帮助，也没有规定时间，学生认为已经完成就上交测试卷，如果认为自己不能解决该问题，也可以上交。

三、测查的结果及分析

通过对测查结果的统计和分析，我们发现学生对于①号方框和②号方框的解答情况基本一致，所以在下面的水平层次讨论中，我们把两个方框的情况一起进行分析。根据答案是否正确，想法是怎样的，我们把学生的回答分成以下5个水平层次。

水平层次具体指标百分比水平0 10.0%水平1 6.7%人数 2 4 2水平2 3.3%水平3 8 7 1 9 31.7%90.0%水平4答案不正确，无视参考点的存在，直接将一小格当作1答案不正确，直接将一小格当作0.1，但数的方法有误答案正确，直接将一小格当作0.1，整数几过去几小格就是几点几答案正确，先考虑区间，然后直接将一小格当作0.1，整数几过去几小格就是几点几答案正确，能从进率或十等分的角度思考46.7%11.7%

水平0与水平1：答案错误，占10.0%。水平0的两个学生（如图1）无视题目中给定的参考点1、2，觉得0的后面相继应该是1、2、3……所以①号方框里填2，②号方框里填12。这样的错误在前测中出现得较多。

图1

水平1的四个学生（如图2）在数的方法上存在错误，他们将0所对的分隔线当作0.1，①号方框箭头所指的分隔线是0.3；将1所对的分隔线当作1.1，②号方框箭头所指的分隔线是1.3。这样的错误在前测中也大量存在。

图2

水平2～4答案正确，占了90.0%。正确率高是否说明学生理解了“数线上标小数”的实际意义？从对具体想法的统计中，我们发现并不是如此。水平2的46.7%的学生认为0或1后面几格就是零点几或一点几（如图3）；水平3的11.7%的学生先考虑箭头所指的位置处于哪两个整数之间（如图4），再按照水平2的方式进行思考。从中可以看出，这些学生并不清楚0.1的意义，但也能成功地给出正确答案。

图3

图4

只有水平4的31.7%的学生能够从相邻两个计数单位间的进率或十等分的角度解决问题（如图5～图7）。

图5

图6

图7

四、测查的结论与建议

（一）结论

本次测查单从结果上看，正确率高达90%，但分析学生的想法，只有31.7%的学生能从相邻两个计数单位之间的进率或十等分的角度思考，说明学生对于在“数线上标小数”的实际能力不容乐观。常犯的错误有三种：（1）忽略数线所给定的参考点，直接将一小格当作1；（2）数格子的方法错误；（3）直接将一小格当作0.1。其中第三种错误最普遍，水平1～3共65%的学生犯了这个错误。

从问卷中学生的想法和对部分错误学生的访谈中得知，错误的学生缺少解决数线问题前先寻找整体“1”和确定将整体“1”几等分的意识。当建议部分学生先找出整体“1”时，又发现他们对在数线上找整体“1”存在困难。

（二）建议

根据以上结论，对教学有以下四点建议。

1.培养学生找整体“1”的意识

从学生的想法中可以看出，水平0～3的学生在解决问题时，没有去分析问题中的整体“1”是什么以及将“1”平均分成几份。在分数的教学中，比较强调把整体“1”进行平均分，分母表示“1”平均分成的份数，分子表示这样的几份。因为教学中强调，所以学生在进行分数的相关练习时能自觉地关注每个问题的整体“1”。在小数的学习中，由于大多数教材是在分数与小数的联系中引入小数的，学生在理解小数时，只关注与分数的对应，而小数的整体“1”往往被忽视。尤其是学到带小数的时候，整体“1”更容易被忽视。

建议教学中教师在加强小数与分数联系的同时，让学生借助多元情境，经历直接描述小数产生的过程，即“将（）平均分成10份、100份……表示这样（）份的数就是零点几或零点零几……”在语言描述中让学生感受到小数的整体“1”和分数的整体“1”同等重要，从而形成自动化的意识，即解释小数意义时先思考该小数的整体“1”是什么。联系到数线问题，在解决问题时第一步应先思考“把（）进行平均分”。

2.凸显十等分的本质

在小数的符号中，整体“1”被等分成多少等份是隐含在数位中的，占多少份由小数点后的部分显示。当整体“1”被分成10的幂次方等份时，才能用小数表示。从测查中了解到，学生很难想到小数符号和10的幂次方等分的关系。这与学生在学习“小数的初步认识”时所接触到的问题情境有关。以人教版教材为例，在“小数的初步认识”的学习中，教材呈现的都是十等分的例子：米与分米、元与角、面积形式的十格图、将整体“1”均分成10份的数线图等。这样的情境，学生即使不懂一位小数的意义，也知道0.2就是涂2格，0.5表示数线中的5小格……所谓“熟悉的地方没风景”，十等分的情境无形中干扰了学生对小数本质的关注与把握。再加上教师在教学上不断强调的对应关系，学生只关注到表示几份，而忽略了整体“1”被平均分成几份。

建议教师在使用教材中列举的十等分的素材后，引导学生对所有的素材进行对比，从而发现使用的素材不同，但都表示把整体“1”平均分成10份、100份……表示其中的若干份，促使学生从对个别具体量的感知跃升为对一类现象的感知。在此基础上增加一些非十等分的问题。如类似图8的判断题，让学生在判断和说理中明晰十等分的重要性。或类似图9的不是等分成10份的数线，在错误答案0.2和正确答案0.4的辩论说理中再一次聚焦十等分。

图8

图9

3.重视表征间的过渡

经历了建议1和建议2的教学后，学生可能对于数线的理解还存在难度。因为之前所接触的线段模型（如图10）和面积模型（如图11），都是把整条线段或整个图形看作整体“1”，小数表示的是线段中的一小段或图形中的一小块。

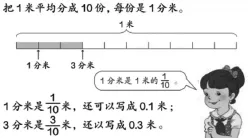
图10

图11

而数线上除了0和1这两个数，还有2、3、4等数的存在，这给学生如何确立整体“1”带来了困惑。另外，数线上的小数表示两种意思：一是表示数与数线上的点之间的一一对应，如①号方框所指的点对应的数是0.1；二是一个数与一段有向线段的对应，如0所对应的点到①号方框所对应的点之间的这一段是0.1。学生之前接触的线段模型和面积模型对表示的第一种意思没有经验积累，对表示的第二种意思有经验积累，但因为数线问题中并没有标出有向线段，学生迁移起来有困难。

建议教师在教学时放慢从其他模型过渡到数线模型的过程，重视表征间的过渡。教师可以进行如下尝试：课件出示一根米尺，让学生用这根米尺量一量彩带的长度（长1.2米）。学生通常会想到两种方法，一是把超过1米的零头单独量，二是在原来米尺的后面再增加一根米尺。量出彩带后让学生继续思考，如果彩带超过2米，怎么办？超过3米呢？课件将4根米尺渐变成数线，并介绍：数线上的0、1、2、3、4……都是以前学过的数，叫自然数。接着课件演示将数线上每一段都平均分成10份的过程，让学生填一填0过去的第一个点用小数表示是多少，并对意义进行追问，即0到1之间被平均分成10份，0.1表示0到这里（教师手指数线上0.1的刻度）的长度，这个点就可用0.1表示。接下去的教学逐步从一份过渡到几份、从纯小数过渡到带小数。这样的教学可以帮助学生顺利地从线段模型过渡到数线模型。

4.指导数格子的方法

经历以上三个建议的教学，学生还有可能像水平1显示的那样数错格子。其实这样的错误并不是第一次出现，学生在一年级上册解决如图12的问题时，会错将钢笔数成7格长，将活动铅笔数成8格长。

图12

一年级下册解决如图13的“纸片有多长”的问题时，会错将纸片数成4厘米长。

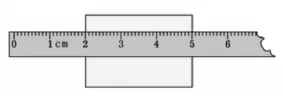
图13

在“方向与位置”单元，描述如图14的4路公交车路线时，会将“4路公交车从光明路向东行驶2站到商场”错数成“行驶3站到商场”。

图14

各个年级都会出现类似的错误，说明教师对此类错误不够重视，也说明对于学生来说此类错误根深蒂固。如何杜绝此类错误的发生？笔者觉得落实数线上的小数表示的两种意思是根本，除此之外可借助边画弧线数格子的方法来突破。如果采用数分隔线的方法，则强调起点不数。