基于LSTM的大棚环境变量预测

陈 亮,裴晓辉,刘韵婷

(沈阳理工大学 自动化与电气工程学院,沈阳 110159)

因为气候变化、人口增加、劳动力减少和食品安全等因素,促使农业寻求更多创新措施来保护和提高农作物产量。目前主流的大棚控制方法是采用农业物联网技术对温室大棚进行智能控制,通过智能传感器对大棚内环境数据进行采集,然后专家系统根据大棚内的环境状况提供控制设备的下一步动作[1]。由于专家系统是根据种植专家的经验来设定的,不能根据实际情况做出实时决策,从长远来看不利于植物的生长。

深度学习的飞速发展为现代农业的进步带来了新的契机,深度学习技术与农业物联网技术的结合可以为植物提供更加适宜的生长环境。深度学习技术能根据大量的历史信息和实时数据对未来进行合理的推断。物联网技术和深度学习技术相辅相成。物联网技术为深度学习提供持续的数据需求,深度学习技术可以处理和从中学习的数据越多,其预测的准确率也会越高。

大棚环境变量数据具有时间序列特征。近年来,随着深度学习技术的不断发展,一些深度学习模型逐渐被应用到时序数据的研究中[2]。在深度学习模型中,循环神经网络(Recurrent Neural Network,RNN)将时序的概念引入到网络结构设计中,使其在时序数据分析中表现出更强的适应性。在众多的RNN变体中,长短期记忆(longshort-term memory,LSTM)模型[3]弥补了梯度消失和梯度爆炸、长期记忆能力不足等问题。近年来,LSTM在故障序列预测[4]、空气污染时空预报[5]、短时交通流预测[6]、铁水硅含量预测[7]等领域取得了良好的预测效果。与传统的RNN相比,LSTM能学习具有长时间跨度的时间序列并自动确定最优时间滞后预测,更有效地利用长距离的时序信息。

本文采用LSTM对温室大棚植物生长环境变量——温度、湿度、二氧化碳浓度进行时间序列预测,通过数据预处理、改进模型网络层数和参数等方法,提高预测精度,协助管理员更好地进行温室环境控制。

1 循环神经网络模型

1.1 标准RNN

图1为标准RNN网络结构图。

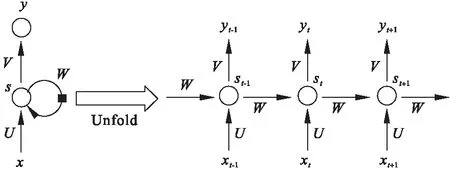
图1 RNN网络结构图

图中x为输入层,给定一个序列xt=(x1,x2,……xt,xt+1)输入到RNN细胞中,根据式(1)、式(2)可计算出一个隐藏层序列st和一个输出序列yt。

st=f(Uxt+Wst-1+bs)

(1)

yt=softmax (Vst+by)

(2)

式中:下标t指时间;f为激活函数;b为偏置向量;V、W、U为权重系数矩阵。

标准RNN能有效地处理非线性时间序列,但存在以下两个问题[8]:

(1)标准RNN不能预处理延迟过长的时间序列(长期依赖问题);

(2)实际应用中训练RNN模型很难自动获取延迟窗口长度的最优值。

为解决上述两个问题,提出了LSTM模型。

1.2 LSTM模型

LSTM是RNN的一种特殊类型[9]，由Hochreiter & Schmidhuber(1997)提出,并被Alex Graves进行了改良和推广。LSTM通过对标准RNN细胞结构进行改进来避免长期依赖问题。

LSTM用三个门来控制单元状态c的内容,其中遗忘门用来决定上一时刻的单元状态c丢弃什么信息,保留哪些信息到当前细胞状态c;输入门用来决定当前时刻网络的输入x有多少保存到细胞状态c;输出门决定当前细胞状态c中的信息有多少被输出。LSTM模型细胞结构[10]如图2所示。

LSTM细胞前向计算方法可以表示为[11]

I=σ(Wxix+Whih+Wcic+bi)

(3)

f=σ(Wxfx+Whfh+Wcfc+bf)

(4)

c=ftc+Ittanh(Wxcx+Whch+bc)

(5)

o=σ(Wxox+Whoh+Wcoc+bo)

(6)

h=otanh(c)

(7)

式中:I、f、c、o分别表示LSTM细胞中的输入门、遗忘门、细胞状态、输出门;h表示当时间为t时LSTM单元的输出;W和b分别对应的权重系数矩阵和偏置项;上标t表示时间;σ和tanh分别为sigmoid和双曲正切激活函数。

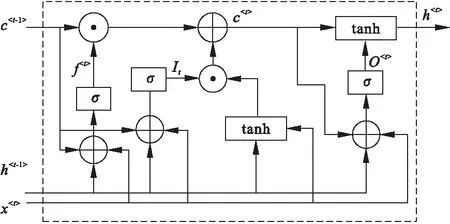
图2 LSTM细胞内部结构图

LSTM训练模型采用的是BPTT算法,大致可以分为四个步骤[12]:

(1)按照前向计算方法公式(3)～(7)计算LSTM细胞的输出值;

(2)在时间和网络层级两个方向上计算每个LSTM细胞的误差项;

(3)按照相应的误差项,计算每个权重的梯度;

(4)选用基于梯度的优化算法更新权重。

2 大棚环境变量预测

根据环境变量时间序列有限样本点的数据特点及循环神经网络从简的设计原则,本文构建的基于LSTM的大棚环境变量预测模型整体框架图如图3所示,框架包括输入层、隐藏层、输出层、网络训练及网络预测五个部分。

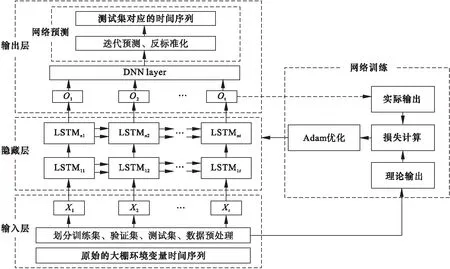
图3 基于LSTM的大棚环境变量预测模型

2.1 数据预处理

原始的大棚环境变量数据的预处理包括对数据中的异常值和缺失值处理以及数据标准化处理。由于原始数据中前后两个时刻的值差值较小,所以对于缺失值和异常值均选取该值前后两个时刻的平均值代替该时刻的值。

对数据标准化操作可加快网络训练收敛速度,提高模型训练的精度,消除范围较大的特征值给梯度更新所带来的影响。本文采用以下方法对数据进行标准化处理。数据标准化用公式表示为

xnorm=(x-xmin)/(xmax-xmin)

(8)

式中:xnorm为标准化后的数据;x为原始数据序列;xmax、xmin分别为原始数据集的最大值和最小值。

2.2 网络训练

网络训练主要针对的是隐藏层。在输入层中,定义原始的大棚环境变量数据序列为

Tn=(x1,x2,…,xt,…,xn)

(9)

式中:xt={at,bt,ct},at、bt、ct分别表示为t时刻大棚环境变量温度、湿度、二氧化碳浓度的值。从Tn中划分训练集、测试集。

Ttr=(x1,x2,…,xm)
Tte=(xm+1,xm+2,…,xn)
1≤m≤o,m、n∈N

(10)

用2.1中的标准化方法处理的训练集、测试集可表示为

(11)

为适应隐藏层输入的特点,构建短时间输入序列,通过固定步长来确定时间序列的长度。设步长取值为L,则模型输入为

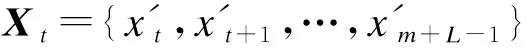
(12)

对应的理论输出为

(13)

将X输入隐藏层,经过隐藏层的输出为

P=(P1,P2,…,Pm-L)
Pt=LSTM (xt,c< t-1 >,h< t-1 >)
1≤L≤m,m∈N

(14)

式中c、h为上个时刻的细胞状态和隐藏层状态。

本文使用均方根误差RMSE作为误差计算公式,用公式表示为

(15)

式中:L(m-L)为训练的样本总数;Pi为预测值;Yi为真实值。

本文通过Adam优化方法更新网络的权重,使网络损失最小。该优化方法的步骤描述为[13]:

(1)初始化参数向量θ0;一阶矩向量λ0=0;初始化二阶矩阵变量v0=0;初始化时间步t=0

(2)循环开始:

(3)t=t+1;

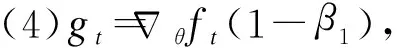
(5)λt=β1λt-1+(1-β1)gt，更新偏差的一阶矩估计;

(6)vt=β2vt-1+(1-β2)gtgt，更新二阶原始矩估计;

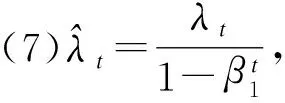
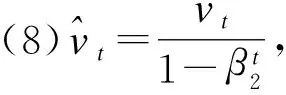
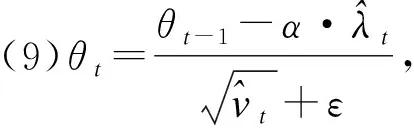
(10)重复(3)～(9),循环直至达到约束条件,结束循环;

(11)返回θt。

其中α为步长;β1和β2为指数衰减速率并位于区间0到1之间;ε为常数;f(θ)为随机目标函数。

针对实际训练中常常存在过拟合的问题,本文采用 Dropout方法来对神经网络进行正则化[14]。由于大棚中环境变量数据量大且变化缓慢,所以在训练过程中以0.1的概率随机丢弃网络中的一些神经元以及相互之间的权重连接,提升模型的泛化能力,不易对训练数据过拟合。

2.3 网络预测

本文采用迭代预测的方法对训练过的LSTM网络进行预测,理论输出的最后L个数据为

(16)

输入训练好的网络LSTM,得到输出为

Pp=LSTM (Yp)=Pm+1

(17)

即m+1时刻预测值为Pm+1,将最后L-1个数据和测试集中的第m+1个数据合并为新的数据并输入网络,得到m+2时刻的输出Pm+2,依次类推得到预测序列为

(18)

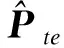
3 实验验证

3.1 实验准备

本文所用的数据来自辽宁省农业研究院大棚农作物西红柿的环境监测数据(温度、湿度、二氧化碳浓度),数据采样间隔为1分钟,共计1440×15个数据点。样本数据划分为二部分:训练集、测试集;比例分别为:90%、 10%;选择RMSE作为模型精度的评估指标。

3.2 模型网络层数和参数的改进

实验过程中,首先确定隐藏层层数,根据数据的特点和经验设置模型参数,选择批次为1440,输入步长为15,学习率为0.03,训练步数为1000。在该模型参数条件下,选择不同的隐藏层层数,通过观察训练集拟合的RMSE和测试集预测的RMSE,确定最佳隐藏层层数。实验结果如表1所示。

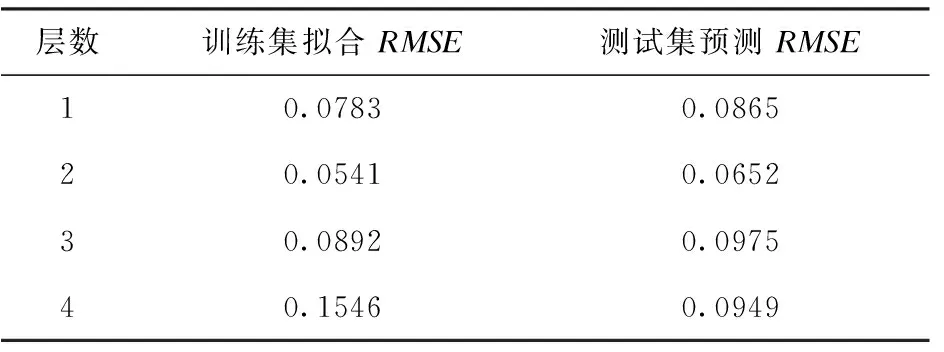
表1 不同隐藏层层数的RMSE对比

表1在四个不同隐藏层层数实验对比中发现,当隐藏层层数为2时,训练和测试样本的RMSE最小,预测精度最高。

所以本文选取隐藏层层数为2的LSTM网络作为本实验的网络模型,在该模型的基础上进一步调节网络参数优化模型。本文主要针对网络模型参数——批次、学习率进行实验,以RMSE作为评价准则,选出网络模型最适合的网络参数。不同网络参数的RMSE对比如图4所示。

由图4可知,不同学习率下,当批次小于720时,训练集拟合的RMSE和测试集预测的RMSE下降速度较快;批次大于720时,训练集拟合的RMSE和测试集预测的RMSE下降速度缓慢。由于批次的增大,训练时间随之增加,综合考虑模型的训练速度和预测精度,本文选择批次为720。当批次为720,学习率0.01和0.03的精度都是在0.05附近,学习率越高,网络收敛速度越快,故本文将学习率设置为0.03。

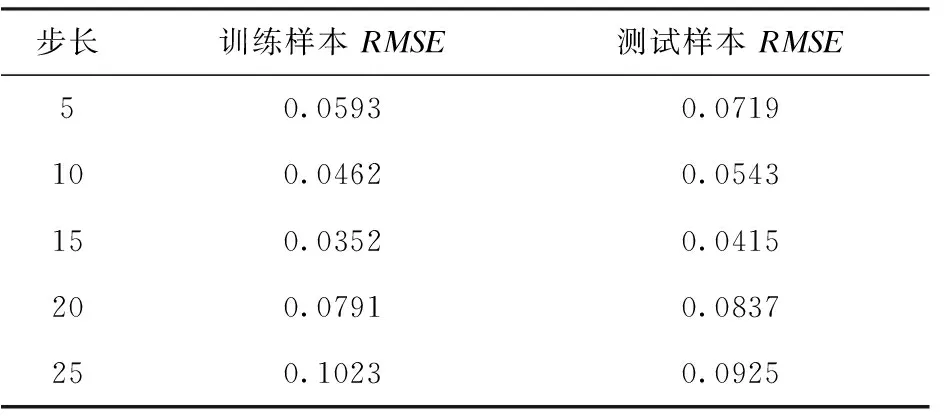
在批次为720,学习率为0.03的实验条件下,对网络输入步长问题进行实验,以RMSE作为评价指标,实验结果如表2所示。

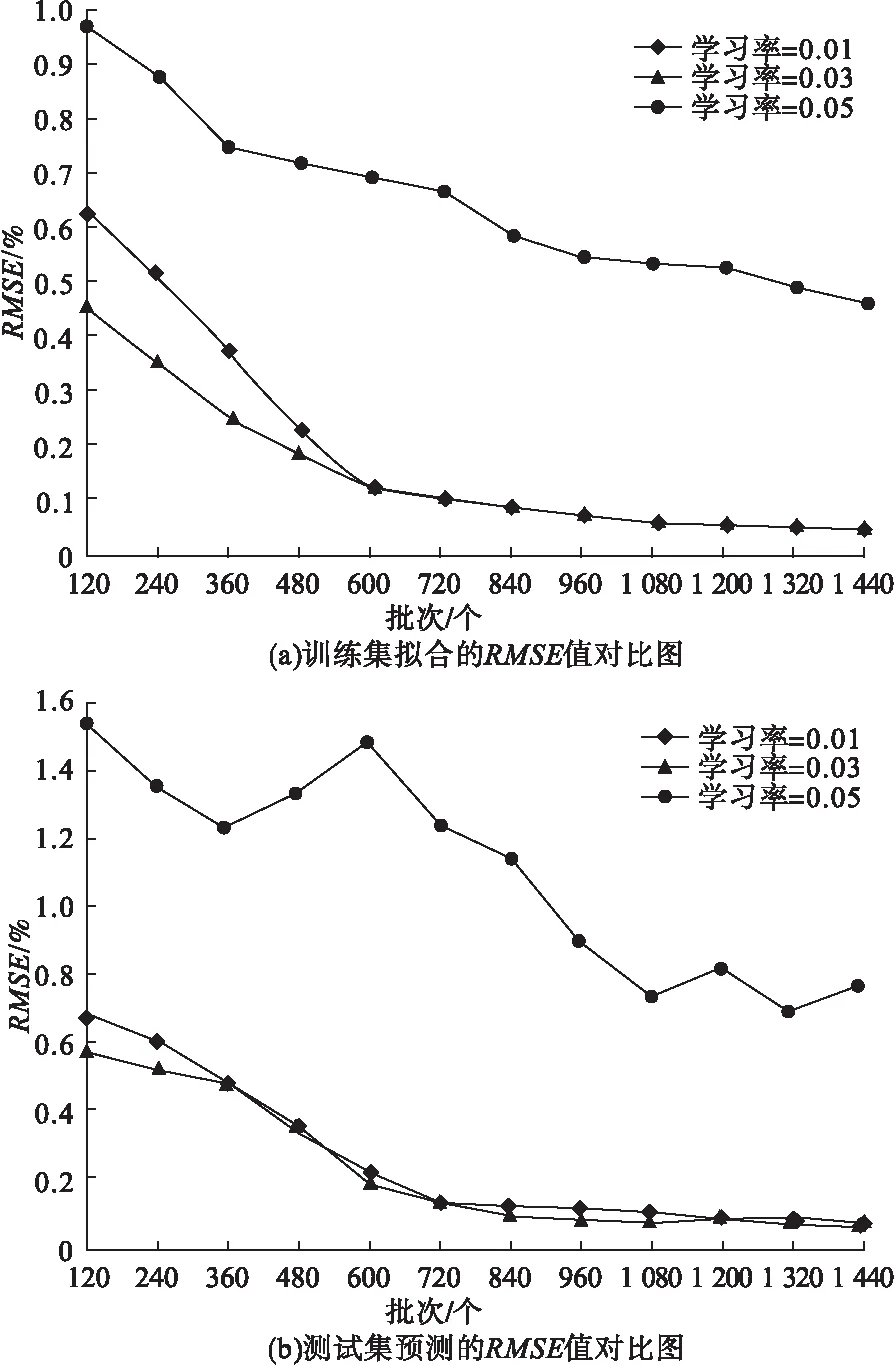
图4 不同网络参数的RMSE对比图

步长训练样本RMSE测试样本RMSE50.05930.0719100.04620.0543150.03520.0415200.07910.0837250.10230.0925

由表2可知,当步长为15时,训练和测试样本的RMSE值最小,网络的预测精度达到最高。所以将步长设置为15。

4 实验结果分析

针对温室大棚种植西红柿的温度、湿度、二氧化碳浓度三个环境变量数据,分别利用LSTM、RNN、GRU对环境变量数据进行预测,图5、图6、图7为测试集若干点的预测结果对比图。

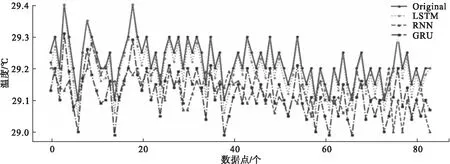
图5 三种不同模型温度预测结果与原始温度数据对比图

图6 三种不同模型湿度预测结果与原始湿度数据对比图

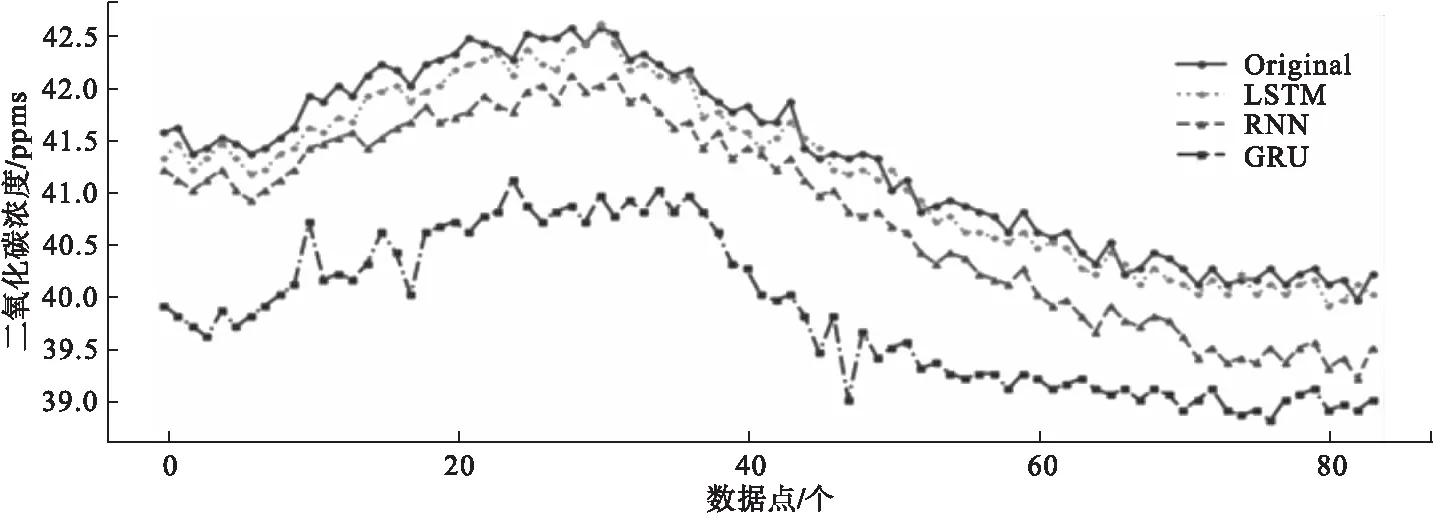
图7 三种不同模型二氧化碳浓度预测结果与原始二氧化碳浓度数据对比图

由图5、图6、图7可以看出,相同参数条件下,采用RNN模型预测出现了较大偏差并且预测趋势与真实温度、湿度、二氧化碳浓度的变化趋势相差较大;GRU模型预测的趋势与原始数据趋势基本一致,但数值仍存在一定的偏差,说明这两个模型预测效果均不是很理想；采用LSTM模型的环境变量预测,其预测趋势与真实趋势基本一致,预测值更接近于真实值,预测效果更好。综上所述,LSTM模型对温室大棚环境变量(温度、湿度、二氧化碳浓度)的预测效果优于其它两种模型,能很好地拟合真实温度、湿度、二氧化碳浓度的变化趋势,达到了比较理想的预测效果。

5 结论

以LSTM为模型,通过模型网络层数和参数选择的方法,以农科院温室大棚的西红柿数据为样本得到训练模型,该模型具有较强的预测和泛化能力,在实际应用中有一定的参考价值,为实现大棚的智能控制提供了理论依据。基于目前的工作,后续可开展进一步的研究,将LSTM温室大棚的环境变量预测模型与温室大棚控制系统相结合,实现大棚的整体智能控制。