基于扩频的复合混沌优选序列生成方法

田明浩,徐晓丹,刘 芳,冯永新

(沈阳理工大学 通信与网络工程中心,沈阳 110159)

目前,混沌非线性动力学系统因具有类似于白噪声的统计特性、确定性、类随机性等特点,并且易产生、易复制、对初始值极端敏感而被广泛应用于扩频通信领域[1]。随着对混沌序列的深入研究,传统一维混沌伪随机序列存在一定的局限性,序列生成方式过于简单,随机性差,复杂性低,容易被敌方破解[2]。因此,如何改善混沌伪随机序列性能成为近年来该研究领域的焦点[3]。鉴于此,本文提出一种复合混沌优选序列,该序列通过用kent映射输出控制chebyshev序列的系统参数,分段logistic映射输出来控制chebyshev映射的初值,chebyshev映射输出再反控分段logistic映射初值,最后将chebyshev和kent序列进行异或得到复合混沌序列,再选取合适的初值及分形参数得到复合混沌优选序列。

通过分析发现该序列提高了序列的复杂度,并且具有良好的平衡性、随机性和相关性。

1 传统一维混沌映射

目前,由于一维混沌映射其产生方式简单,生成序列众多而被广泛应用于扩频通信中,现在比较常见的、统计性能较好的一维混沌映射主要有以下3种,其表达式以及初值和系统参数的取值范围如下。

(1)a阶chebyshev映射的表达式为

Xn+1=cos(acos-1Xn),-1≤Xn≤1

(1)

式中：初值Xn的取值范围为[-1,1]；Xn+1是系统输出；系统参数a取值范围是a≥2时,该混沌系统处于混沌状态,当a≥4时该系统达到满映射状态[4]。

(2)Kent映射的表达式为

(2)

式中：初值Xn的取值范围为(0,1)；Xn+1是系统输出；系统参数a取值范围在(0,1)时,该混沌系统处于混沌状态,根据文献[4-5]可知,在a=0.4997时的混沌状态最好[4-5]。

(3)分段logistic映射的表达式为

(3)

式中：初值Xn的取值范围为[-1,1]；Xn+1是系统输出；系统参数a取值范围在(0,2]时,该混沌系统处于混沌状态,经过实验可得,该系统在a∈(1.8,2]时都可以达到满映射的状态[6]。

2 复合混沌优选序列产生方法

基于上述三种一维混沌映射作为扩频伪随机序列数量众多,统计特性较好,但其实现方式单一,复杂度低,随机性较差的特点,提出了一种复合混沌优选序列,其产生原理是:将chebyshev映射和分段logistic映射进行初值互控,并采用kent映射对chebyshev映射进行参数控制,再将二者的输出进行异或生成复合混沌序列,经过实验,选取合适的初值以及分形参数,得到复合优选混沌序列。其原理框图如图1所示。

由图1看出,该混沌系统可以看作由三大部分组成,第一部分为初值控制模块,第二部分为参数控制模块,第三部分为叠加模块。基于 chebyshev映射的初值和分形参数的取值范围都比较广,所以选用其作为中心序列,其初值和分形参数分别由分段logistic映射和kent映射控制,这里初值和参数是根据查阅文献和大量实验筛选得出的。

在第一部分，中由于分段logistic映射的初值取值范围和chebyshev映射的初值范围相同,所以选用分段logistic映射的输出来控制chebyshev映射的初值,为增加序列的不可预测性,用chebyshev映射的输出反控制分段logistic映射的初值,给定分段logistic映射初值为0.76,系统参数为2。

第二部分中采用均匀性较好的kent映射控制chebyshev映射的分形参数,来增加参数的多变性,给定kent映射的初值为0.76,系统参数为0.4997,chebyshev映射的系统参数设置为ac=4+4f1。

第三部分中将chebyshev映射的输出与kent映射的输出进行二值化后异或,既产生了复合混沌优选序列。

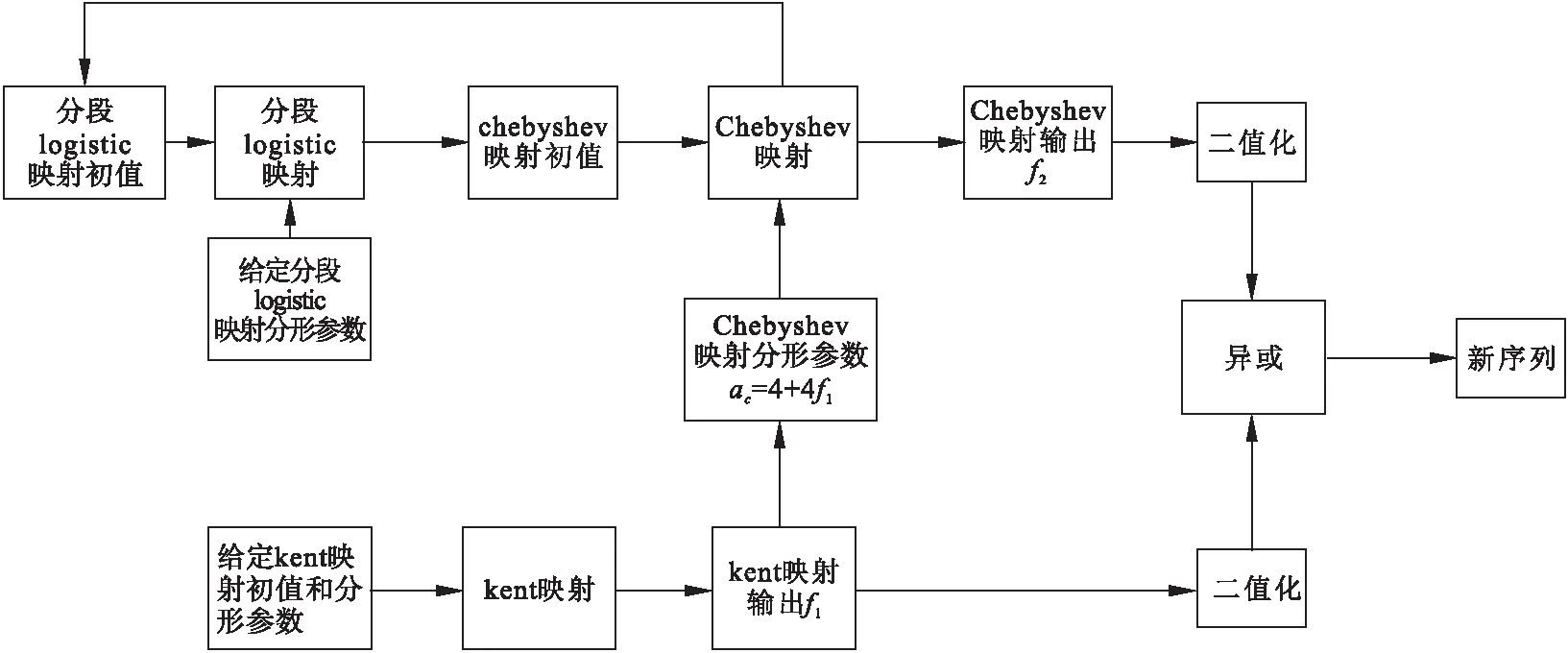
图1 复合混沌优选序列原理框图

3 复合混沌优选序列的性能分析

通信系统中伪随机序列性能的好坏会影响通信系统的性能[7-8],而伪随机序列的性能主要由复杂度、平衡性、游程特性、相关性和随机性这几个特性来体现,其中,平衡性、游程特性和相关性可以归为PN序列(Pseudo-noise Sequence)检验,所以复合混沌优选序列作为混沌伪随机序列,也要分析这些特性。

在理论分析的基础上,基于Matlab 2015a 仿真软件,使用Matlab语言对序列的复杂性、PN序列检验和随机性等方面进行分析验证,这里的PN序列检验指的是对序列的平衡性、游程特性和相关性进行检验。

3.1 复杂性分析

序列的复杂性会影响序列的随机性和不确定性；复杂度越高,随机性和不确定性越好。序列的复杂性可用近似熵(approximate entropy，ApEn)来衡量[9-11],不同序列长度对序列复杂性的影响以及不同混沌序列的复杂性情况如表1所示。

表1 序列复杂性

由表1中可以看出,随着混沌序列长度的增加,混沌序列的复杂度增加,并且同一序列长度下混合混沌序列的ApEn值最大,即它的复杂度最高,表现出了更好的随机性和不确定性。

3.2 PN序列检验

PN序列检验就是检验混沌序列作为伪随机序列是否满足Golomb提出的三点随机性公设,分别是平衡性、游程特性和相关性[12]。

因为序列的平衡性和载波抑制度有密切联系,平衡性差的序列会导致载波泄露,易使信息暴露、丢失、被截获、破解等,所以一般要求混沌伪随机序列的平衡度E<0.02[13]。混沌序列在初值范围内平衡度的平均值如表2所示。

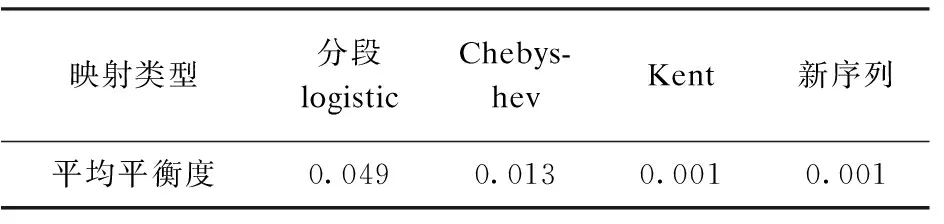
表2 平衡度均值

由表2可以看出,复合混沌序列有均衡的0-1比,并且满足E<0.02的要求,满足Golomb伪随机假设的第一条件。

游程特性是表征码序列随机性的一个重要方面,表3是混沌序列的游程统计结果,混沌序列长度L设为3000。

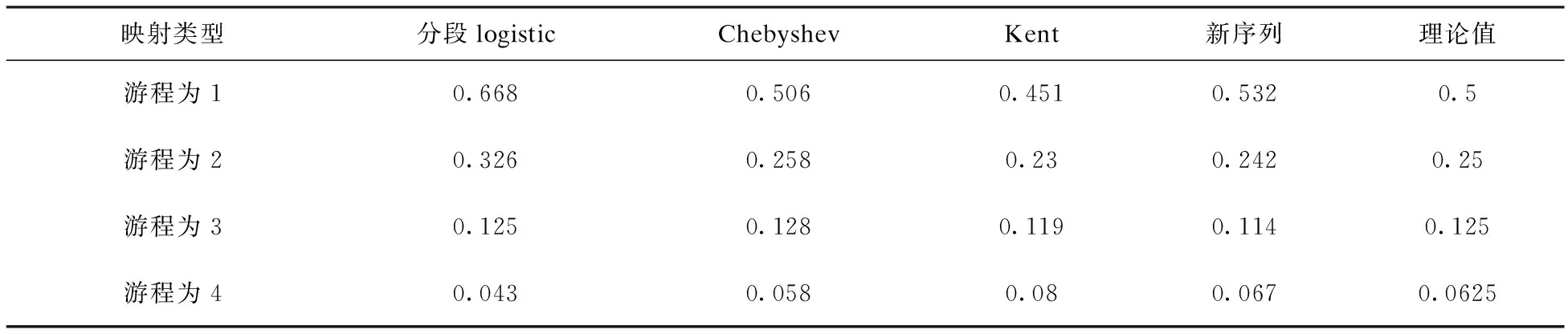
表3 序列游程特性

由表3可以看出,序列长度为L的“0”串和“1”串个数大致相等,且占整个二进制序列总游程个数的1/2L,满足Golomb伪随机假设的第二条件。

因混沌伪随机序列的相关性对通信系统非常重要,要分析的因素较多,所以下面要对混沌序列的相关性展开具体的分析。

混沌序列作为伪随机序列,要有良好的相关性能,自相关值需近似于δ函数,以利于扩频码的检测与同步；而互相关值需接近于0[13],以有效地抑制不同扩频码之间的干扰,这对通信中的多址应用十分重要[14]。理论中无限长度的混沌序列能满足上述条件,但实际上混沌序列使用时都需要截短处理,这样会影响混沌序列的相关性。除此之外,混沌序列的初值也会影响序列的相关性,经过大量测试后发现复合混沌序列在初值为0.76时的相关性能较好,所以以此初值产生的混沌序列来进行测试。

(1)自相关性

设混沌序列S的长度为N,则自相关函数为[15]

(4)

式中:k为序列点;n为偏移点数;R(n)为自相关峰值。

自相关峰值最大值[15]

(5)

式中Rmax为自相关峰值最大值。

自相关旁瓣最大值[15]

(6)

式中Rmax1为自相关旁瓣最大值。

图2为复合混沌序列和几种一维混沌序列在不同序列长度下的自相关峰值比的对比图。

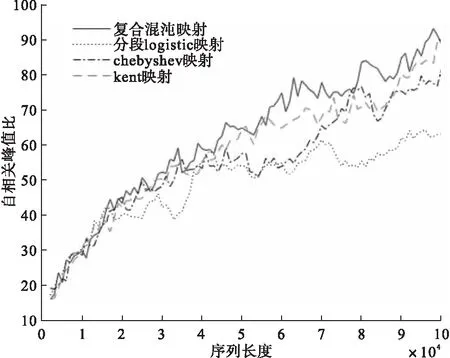
图2 序列长度对自相关峰值比的影响图

由图2可看出,几种混沌序列的自相关峰值比都随着序列长度的增加而逐渐增大；在较短的长度下,几种混沌序列的自相关峰值比相差较小；随着长度的增加,渐渐出现差异,并且,复合混沌序列的自相关峰值比逐渐高于其它混沌序列,表现出良好的自相关性。

(2)互相关性

设混沌序列S1和S2的长度为N,则互相关函数为[15]

(7)

式中：k为序列点；n为偏移点数；C(n)为互相关峰值。

互相关峰值最大值为[15]

(8)

式中Cmax为互相关峰值最大值。

互相关均方值为[15]

(9)

式中σc为互相关均方值。

图3、图4分别为复合混沌序列和几种一维混沌序列的互相关最大峰值及均方值在不同序列长度下的变化曲线图。

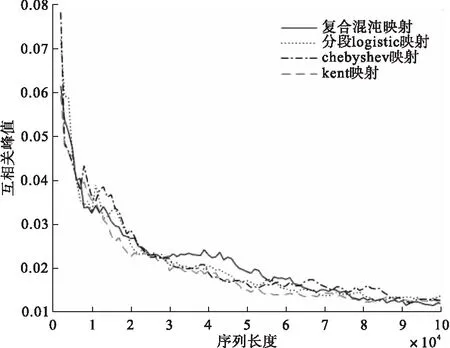
图3 序列长度对互相关最大峰值的影响图

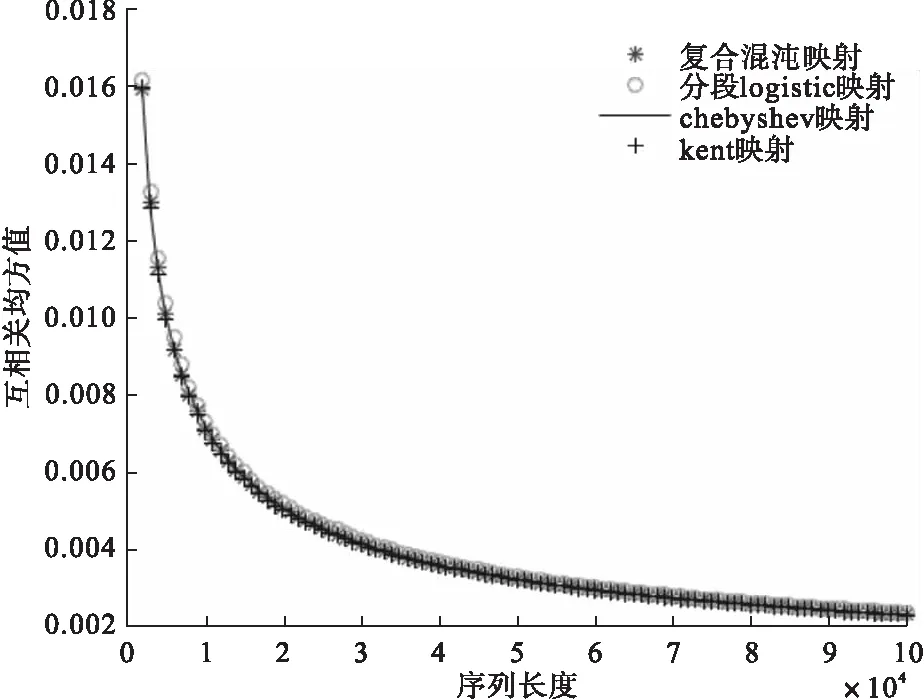
图4 序列长度对互相关均方值的影响图

从图3的整体趋势可看出,随着序列长度的增加,这几种混沌序列的互相关最大值都越来越接近于零,复合混沌优选序列的互相关最大值与其它序列相差不大,且大部分处于其它序列下方。

从图4可看出,这几种序列的互相关均方值基本相同,并且整体趋势都是随着序列长度的增加越来越接近于零。

这两个图说明复合混沌优选序列同样具有良好的互相关性。

结合以上分析,复合混沌优选序列具有类似δ-like的性质,其自相关函数有尖锐的相关峰,互相关峰值接近于零,说明复合混沌序列的相关性能良好,满足Golomb伪随机假设的第三条件[15]。

3.3 随机性分析

除上述性能检验之外,作为伪随机序列,还需要检验其随机性。在通信系统中,序列随机性能跟系统的信息安全性能息息相关,随机性能良好的伪随机序列,系统的信息安全性也好。因此对混合混沌序列也要进行随机性分析[16]。

检验复合混沌序列的随机性能常用的是NIST测试[17],由确定系统和算法产生的序列,最主要的测试包括其频数测试、游程测试、谱测试和近似熵测试[18]。按照NIST测试的要求,为保证测试结果的可靠性和准确性,每个被测序列的长度应为103～107。因此,选取每个序列长度为106[19]。

表4是混沌序列的随机性测试结果.

由表4可以看出,分段logistic映射和kent映射部分测试项没有通过；chebyshev映射虽然通过全部测试,但测试值较低；而复合混沌映射不仅完全通过了这几项测试,并且每一项测试值都高于其它混沌序列,说明复合混沌映射的随机性更好。

表4 随机性能测试结果

4 结束语

针对单一的一维混沌伪随机序列实现简单、复杂度低、随机性差、在扩频通信中容易被反向破解的问题,本文提出用多种一维混沌映射相互控制并进行异或叠加的方法,构成一个复合混沌优选序列。对比于单一的混沌序列,这种多映射的参数互控的复合混沌优选序列不仅明显提高了序列的复杂度和随机性,而且也满足PN序列检验的要求,能够作为伪随机序列应用到扩频通信中。