《用字母表示数》教学实录

刘 瑾

【教学内容】

人教版五年级上册第52～54页。

【教学目标】

1.使学生学会用含字母的式子表示数量，培养学生抽象概括的能力。

2.让学生理解用字母表示数的意义，感悟身边处处有数学，初步体会数学的价值。

3.初步学会从数学的角度提出问题、理解问题，并能综合运用所学的知识和技能解决问题。

【教学重、难点】

重点：会用含字母的式子表示数；难点：理解用字母表示数的意义。

【教学过程】

一、引入

师：（出示课件）这是什么？

生：月历卡。

二、展开

师：同学们，像这样的情况多吗？你能想个办法用一个这样的格子把所有的情况都表示出来吗？请静静地思考一下。

1.活动。

师：请拿出老师给大家准备好的学习单和记号笔，根据老师的要求想一想、写一写。

（学生反馈）

师：大家觉得几号作品表示出了所有的情况？还有吗？

生：2号和3号作品。

师：1号和4号为什么不行？说说你的理由。

生：这两幅作品只表示出了一种情况。

师：我特别想采访一下2号作品和3号作品的同学，你们是怎么想的？

生：（2号作品）我是想把每个方格可以表示的情况都列举出来。

生：（3号作品）我认为用数字和一个字母就可以把所有的情况都列举出来。

师：同学们觉得3号作品把所有的情况都表示出来了吗？为什么用字母能表示出所有的情况呢？用字母可以表示出1号、4号作品的情况吗？还可以表示出哪些情况？原来用字母可以表示出任何一种情况。

师：如果要在2号和3号作品中选择一个你选哪个？为什么？

生：我选3号作品。因为这样表示很方便。

师：原来用字母表示数这么厉害！

（教师板书：概括、简洁）

2．揭题。

师：这节课我们就来研究“用字母表示数”。

3.字母的范围。

师：其实老师和大家的想法是一样的，我也是用字母来表示的，只不过我用了a来表示。除了用a，还可以用什么字母？

生：所有的字母都可以。

师：同学们，在这个月历表中，a有限制吗？哪些不行？

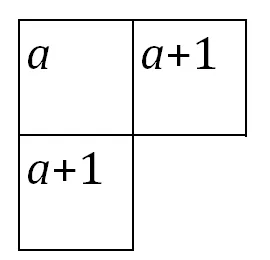
生：a是有限制的，a必须大于或等于1还要小于或等于24。

师：说明这个a是有范围的。

［板书：范围数（多个）］

师：以下这两个例题中的a的范围是什么数呢？

例1：一条绳子长a米。

［板书：任意数（无数个）］

例 2：2.1， 2.3， 2.5 ， a，2.9， 3.1。

［板书：特定数（一个）］

小结：都是a，但是情况不同，所以表示数的范围也不一样。

4.对比数量关系。

师：刚才同学们都赞同用字母来表示数，我还想到了这样的方法。

师：这样可以吗？为什么也可以？（同桌讨论）

师：这里的c可以表示什么？8可以吗？25可以吗？a+7可以表示这里的所有数吗？看来这两种方法都可以表示这里所有的数。

师：如果要从这两个里面选择一个，你选哪个？为什么？

师：a+7好在哪里？

小结：看来a+7不仅能表示数，还能表示出数量之间的关系。

（板书：数量关系）

师：为什么a+7能表示出数量关系，c就不行呢？它们之间有什么区别？（板书：字母式）

师：如果我想表示c与a之间的数量关系，怎么办？

生：规定c=a+7。

5.变式。

师：刚才我们用a来表示第一个数，如果我们像下面这样表示可以吗？

出示：

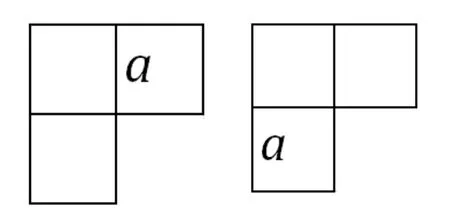
师：其余的两个数你会填吗？这时候三个数之间的关系还一样吗？或者是怎样的关系？

小结：用a表示这三个数中的哪个数都可以，但是这三个数之间的数量关系不变。

6.找关系。

师：同学们能帮老师找找这些球之间的关系吗？

师：你会说它们之间的关系吗？你还能怎么说？

师：同学们，其实我们很早就已经接触字母了，不信你来看。

如果用今天的知识来改，你想怎么改？（a+a+a=18）用a+b+c=18可以吗？为什么？那用b+b+b=18可以吗？这里的a是什么数呢？那a等于几？

（2）说说下面运算定律表示的意思。

加法交换律 a+b=b+a

加法结合律 （a+b）+c=a+（b+c）

乘法交换律 ab=ba

乘法结合律 （ab）c=a（bc）

乘法分配律 （a+b）c=ac+bc

师：这里的字母可以是什么？

（3）C=4a，S=a2。

师：请同学们猜猜这两个式子表示什么？

出示：（下图）

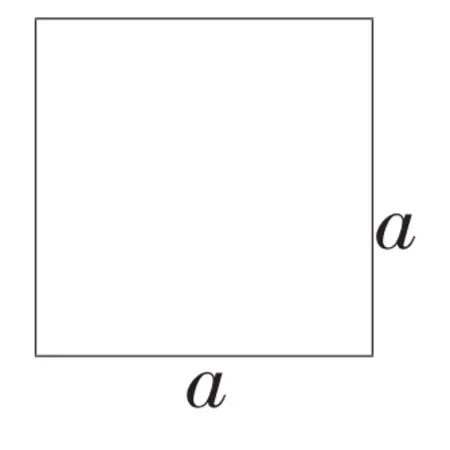
师：现在能猜出来了吧？如果a等于6，你会算周长和面积吗？

师：你能模仿着说说正方形的周长和面积吗？

小结：看来用字母还可以表示运算定律和计算公式。

三、回顾

师：这节课我们一起研究了用字母表示数，同学们能回答老师两个问题吗？

问题一：我们为什么要用字母来表示数？

问题二：用字母可以表示哪些数？还可以表示什么？

四、介绍韦达

师：你知道最早有意识地使用字母来表示数的人是谁吗？他就是法国数学家韦达。韦达一生都致力于数学的研究，做出了很多重要贡献，成为那个时代最伟大的数学家。自从韦达系统使用字母表示数后，引出了大量数学发现，解决了古代的许多复杂问题。