多元表征促理解对比分析悟本质——《分数的意义》教学设计与解读

胡萌洁

【教学内容】

人教版五年级下册《分数的意义》。

【教学过程】

一、唤醒经验，多元表征呈现原认知

师：今天我们一起学习分数的意义，同学们认识分数吗？你对分数有哪些了解？

（学生回答略）

师：请在这张纸上写下你的想法，可以画一画、写一写或列一列算式。可以自己创作，也可以用老师提供的素材。

（学生自主创作）

【设计意图：分数的意义在学生脑海中并不是空白的，原有知识的唤醒有助于对学生认知起点的把握，而个性化的表征方式有助于呈现不同的思维水平。】

二、沟通表征，分类对比凸显本质概念

1.对比不同类型的图形表征，初步建构分数意义。

（学生解读作品）

师：不管是一个图形、一堆物体还是一条线段，把它们平均分成4份，这样的3份都能用来表示。有一位同学是这样描述的：就是由“1”平均分成4份，取其中的3份。

【设计意图：第一组作品中包含图形表征、符号表征和文字表征，图形表征提供直观模型，符号表征避免了冗长的叙述，文字表征清晰地描述对象的意义与内涵，通过对不同表征的对比有助于学生进一步感知分数的本质意义。】

2.对比等值分数的图形表征，丰富分数意义的内涵。

师：4在哪儿？3在哪儿？

师：虽然平均分的方法和份数不同，但都可以看成平均分成4份，有这样的3份，所以也能用来表示。

【设计意图：第二组作品中，呈现的是三幅等值分数的图形表征。其中图①图②可以根据分数的意义直接判断，图③需要通过讨论才能确定，只要添加一条辅助线，就能一眼看出它依然是平均分的，从而建立“6份和8份”与“3份和4份”的联结，为今后学习“等值分数”和分数的基本性质做铺垫。】

3.对比不同单位“1”的图形表征，深化对单位“1”的理解。

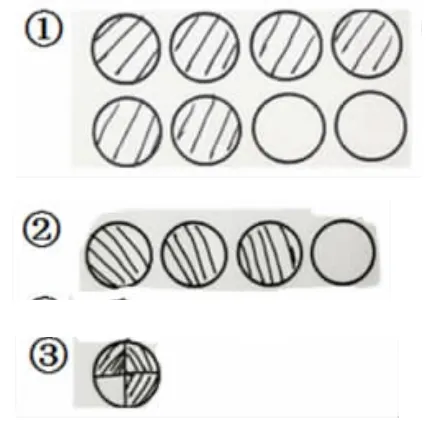
（学生独立思考）

（学生同桌交流）

师：谁来当当小老师，上来一边指一边说。

生：因为被分的圆的数量不一样。图①分的是8个圆，图②分的是4个圆，图③分的是1个圆。

师：同学们听懂了吗？谁也想来说一说？

生：因为分的数量是不一样的，所以结果也是不一样的。

师：是的，我们平均分的对象既可以是1个圆，也可以是1堆圆，它们都可以看成一个整体，一个整体可以用自然数“1”表示，我们把它叫做单位“1”。

【设计意图：第三组作品提供了不同单位“1”的图形表征。通过图形表征的对比，形成强烈的直观视觉冲击，引发思考。然后通过对作品实际意义的分析和对比，感受到分的对象不同，分的结果也不同，从而理解单位“1”在分数中的重要作用。】

4.对比相异分母的图形表征，理解分数单位的意义。

师：同样是三份，为什么要用不同的分数来表示呢？

生：因为它们每一份的长度不一样。

生：因为图①是平均分成4份，图②是平均分成5份。

师：平均分的份数不一样，分出来的每一份也不一样。图①中的一份用来表示，图②中的一份用来表示。这里的我们把它们叫做“分数单位”。

师：就像长度单位一样，规定了1厘米的长度，我们就以1厘米为标准，去量别的物体，有几个1厘米就是几厘米。

【设计意图：第四组呈现了不同分数单位的两幅作品。通过对比，将学生的注意力集中在对分数单位的理解上，感知分数单位对分数意义的重要作用。同时与长度单位“厘米”进行比较和沟通，帮助学生把对长度单位的认知迁移到对分数单位的认知，其本质都是用单位量的累加进行度量。】

三、对比练习，加深对意义的理解

1.小试牛刀，巩固新知。

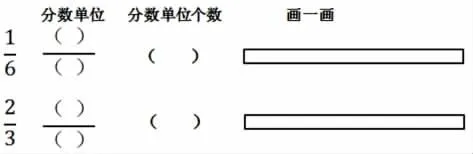
【设计意图：本题作为基础巩固练习。通过写一写、画一画的方式巩固和检测学生对单位“1”和“分数单位”的认知，加深学生对分数意义的理解。】

2.反向比较，提升思维品质。

说一说，被藏起来的水果分别有几个？

【设计意图：本题作为变式思辨练习。通过反向的变式练习再次帮助学生深化对单位“1”的理解。逆向思维可以帮助学生打破固有的思维方式，对学生的认知水平提出了更高的要求。】

3.分类建构，完善认知结构。

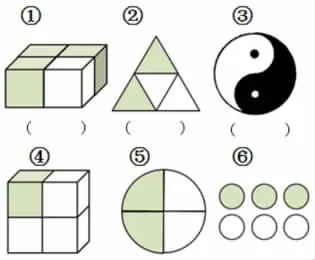
要求：

（1）看图，用分数表示各图中涂色部分的大小。

（2）根据分数的意义分类。

（3）小组讨论，并向你的组员说明你的判断依据。

（4）选出一位汇报人。

生：①②④⑤一组，③一组，⑥一组。因为①②④⑤的分数单位相同，都是

生：②③⑤⑥一组，①一组，④一组。因为②③⑤⑥分数值相同，涂色部分都表示整体的一半。

【设计意图：作为分类建构练习，通过分类对比，让学生的知识体系更具结构性和序列化。这组练习中既有平面图形表征也有立体图形表征，既有连续量表征也有离散量表征，既有规则图形表征也有不规则图形表征。如此丰富多元的表征设计有助于学生拨开形式的外壳，聚焦认知的重难点，认识到分数概念的本质，也是对整节课的回顾与反思。同时相对开放多样的分类方法也有助于不同学生的个性化发展，培养学生灵活、发散的思维习惯。小组合作的学习模式让每位学生都有自我表达、互相学习的机会，让学生在交流碰撞中完善思路，在生生互助中学习成长。】