三角形中位线定理教材设计之我见

吴增生

（浙江省仙居县教育局教研室）

一、问题的提出

在2017年举行的第十届初中数学青年教师优秀课展示与培训活动中，三角形中位线定理作为初中几何的重要定理，作为指定内容由六位教师展示和讲述了这一定理的课堂教学过程，以推动这一定理的教学研究.笔者在活动中观察了一个分会场的两位选手对三角形中位线定理的课堂教学及其讲述，发现其教学中存在一些问题.进一步研究发现，教材内容的呈现方式深深地影响着教师的教学行为，从教师的教学过程反映出教材对这一内容的编排可以做更进一步的优化.

二、课例研究

1.两个课例的教学基本思路呈现

两个课例的教学思路基本相同，只有具体的问题和细节稍微不同.

（1）创设情境，提出问题.

两个课例都是通过提出一个测量问题来引入课题.

课例A的现实问题引例是：如图1，某管线的一段AB被污染，现要抢修需测量出AB的长度，但有建筑物被挡，你有办法解决吗？

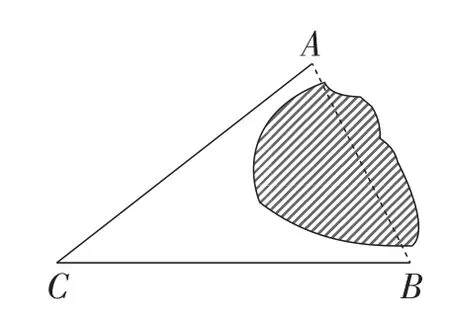
图1

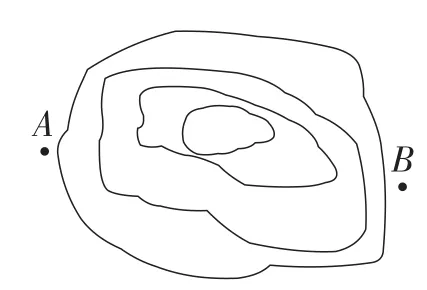
图2

课例B的现实问题引例是：如图2，一条输电线路需跨越一个池塘，池塘两侧A，B处各立有一根电线杆，但利用现有皮尺无法直接量出点A，B间的距离，请你设计一个方案，测出A，B两点间的距离，并说明理由.

两个课例都是先引导学生构造全等三角形来解决问题，再提出是否有更简便的方法解决这个问题，并指出通过本节课学习三角形的中位线后，就可以简便地解决这个实际问题，从而引出学习的主题.

（2）动手操作，探索和发现结论.

两个课例中，教师都让学生动手操作，尝试把一张三角形纸片剪成四个全等的三角形纸片.学生通过尝试，想到需要画三角形两边中点的连线，于是得到三角形的中位线，提出研究中位线的问题.在给出并辨别三角形中位线概念后，教师又让学生“剪一刀，把三角形纸片剪拼成一张平行四边形纸片”，在此基础上引导学生发现三角形中位线的性质.

（3）演绎推理，证明性质.

两个课例都引导学生先把文字命题通过画出图形，写出已知、求证，具体化为直观的线段关系，然后引导学生分析并证明定理的思路，让学生独立书写证明过程，并通过交流提出定理的不同证明思路.课例A是按照如图3所示的几种方式作辅助线来证明三角形中位线定理，即已知D，E分别为△ABC的边AB，AC的中点，求证DE∥BC，且；课例B则介绍了如下的证明思路：（1）作平行线，证明三角形全等，证明平行四边形；（2）旋转三角形后，证明三角形全等，证明平行四边形；（3）中点线段加倍后连续证两次平行四边形.

图3

（4）应用定理解决问题.

证明定理后，两个课例都让学生解决本节课开头提出的实际问题，并进一步研究了中点四边形.课例B还让学生研究四边形的一组对边中点及对角线中点构成的四边形（如图4）的特点.最后，都让学生总结了本节课学习的内容、研究的方法等.

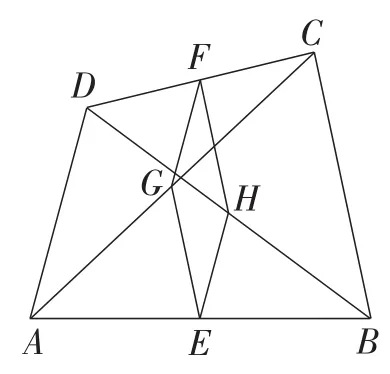
图4

2.课例中存在的问题

（1）创设的情境无法引导学生自然合理地发现和提出问题.

通过创设现实的、有挑战性的问题引发学生的认知冲突，激发学习动机，这是一种引入新课的重要方法.如果仅仅从三角形中位线定理这一知识点的学习来说，这样引入是无可厚非的.然而，如果从知识之间的关联，用系统和整体的观点分析，就值得商榷了.《义务教育数学课程标准（2011年版）》（以下简称《标准》）中，把三角形中位线的内容放在四边形的条目下，表明了运用平行四边形知识探索并证明三角形中位线定理的编写意图，这一意图也在各种版本初中数学教材中得到体现.如果从这种关联性出发，则需要设计与平行四边形有关的提出问题的思路，让学生顺着平行四边形的研究，自然合理地发现、提出、分析和解决问题，而不是另起炉灶，创设新的现实情境.

（2）动手操作活动不自然且难以完成.

两个课例在用现实问题创设认知冲突情境后，马上都转到让学生操作“把一张三角形纸片分成四个全等的三角形”活动，这个活动既来得突然，学生又难以完成.首先，学生不知道为什么要做这个活动；其次，要完成这个操作，需要建立在学生知道三角形中位线定理结论的基础上，否则，学生是想不到“过两边中点沿着直线剪”这种方法的，有逻辑循环之嫌.笔者用举手方式在现场调查了30多位参加会议的且使用同版本教材的教师，问他们“没有三角形中位线知识做基础，学生是否能完成这个操作？”，结果有26人表示“学生想不到”，说明这一操作活动在教学中无法引起学生自然、合理的进行数学思考.

三、教材的研究

为什么两个课例的教学思路惊人地相似，且出现相同的教学问题？进一步调查发现，这两个课例是基于同一版本的教材进行教学的，上述教学思路正是来源于该版本教材的设计思路.这说明教材对教师教学行为具有重大影响，同时说明教材的编写责任重大，需要不断研究并改进教材的建设，使之能承担起引领教师的数学教学，促进数学教学发展现实的核心素养，落实数学育人的使命.

1.现行教材中三角形中位线定理内容的基本呈现方式

对于三角形中位线定理，所有的教材都是放在四边形的内容下，体现应用平行四边形知识研究新问题的编写意图，大部分是放在平行四边形的判定内容学习后（如人教版、浙教版、北师大版等），也有放在特殊的平行四边形学习后（如青岛版）.定理内容的呈现方式基本有两种：一种是直接给出三角形中位线定理的内容，再让学生证明定理；另一种是设计一些操作性探索（如剪纸），体现定理的探索过程.现行各种版本教材中，对三角形中位线定理的安排，对探索过程的呈现并不理想，要么没有呈现其探索过程，要么探索过程不自然，这是什么原因造成的呢？

2.数学史的考证与《标准》研究

为了追溯教材对某一数学内容的编排在引领教学实践中存在问题的原因，考察其形成和发展历史是一种比较有效的方法.其实，在古代两河流域，人类就发现了比三角形中位线定理更一般的结论——平行线分线段成比例定理，它来源于现实生活中土地与财产分割.古巴比伦时期（公元前1800年—公元前1600年）的数学泥版MLC1950上载有以下问题：三角形高为50，用平行于底边的直线将其分割成高分别为30和20的小三角形和梯形，求原来的三角形及分割得到的小三角形的底边的比.用中位线来分割三角形，只不过是其中的特例而已.在欧几里得《几何原本》中，也没有找到三角形中位线定理，只有如下更一般的定理：如果一条直线平行于三角形的一边，则它截三角形的两边成比例线段；又如果三角形的两边被截成比例线段，则截点的连线平行于三角形的另一边.

这一命题其实是对泥版MLC1950上平行线分线段成比例定理内容的一般化推广和逆向研究的结果.

《标准》中，三角形的中位线定理是安排在四边形内容中的，要求探索并证明，而平行线分线段成比例定理作为相似三角形判定的基础，是用基本事实（扩大了的公理）出现的，要求学生掌握.《标准》中的平行线分线段成比例定理比欧几里得《几何原本》的命题更一般，但对逆命题没有要求.

这种分散的安排体现了降低难度和够用即可的意图，但也给教材系统、有序地安排三角形中位线定理及平行线分线段成比例定理带来了困难，难以像数学先贤一样基于现实的面积分割需要，自然、合理地发现、分析和解决问题，从而进行系统的、自然合理的思考和研究.这是造成教材中探索三角形中位线定理设计不够自然合理的重要原因.

四、对三角形中位线定理内容设计的改进建议

既然从数学史的角度挖掘三角形中位线定理的探索活动由于《标准》要求的变化无法进行系统优化，比较现实的做法应该是基于《标准》的要求和意图，把三角形中位线定理放到平行四边形内容中，作为平行四边形研究的自然延伸是一种可选的策略.如果把三角形中位线定理的图形基本结构绕着中点D旋转180°就可以得到▱BCAF（如图5），线段GE就是过平行四边形对角线AB中点D和边AC中点E的一条直线被对边AC及BF截得的线段，而研究过平行四边形对角线中点的直线被一组对边截得的线段的性质，则是平行四边形对角线性质研究的一般化，这在教材的平行四边形内容的例、习题中经常出现，也是学生所熟悉的.把上述过程颠倒过来，就可以融合平行四边形的研究，设计出三角形中位线定理的自然合理的探索发现活动，而且也能为定理的证明提供有效的启发.融合三角形中位线定理和平行四边形研究，对定理探索活动的改进建议方案设计如下.

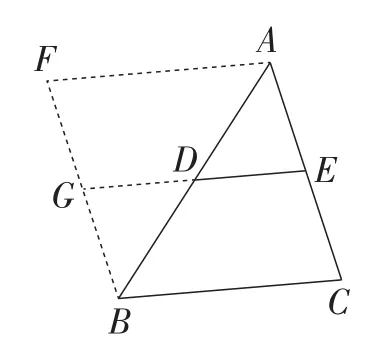
图5

课题：三角形的中位线定理.

我们知道，平行四边形的对角线互相平分，你能探索下面更一般的问题吗？

思考：1.如图6，过▱ABCD的对角线AC的中点G的直线交一组对边BC，AD于点E，F，则线段EF与AC有什么关系？证明你的结论.

2.如图7，如果把点E的位置特殊化，变成边BC的中点，则线段EF与边AB有什么关系？

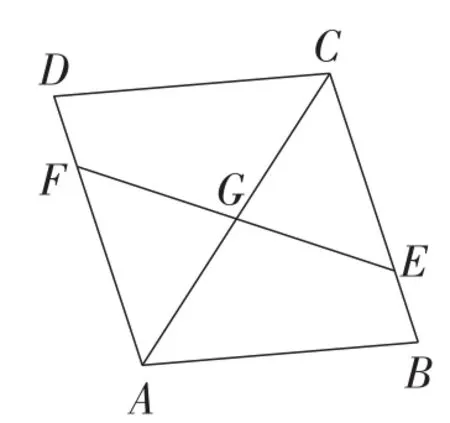
图6

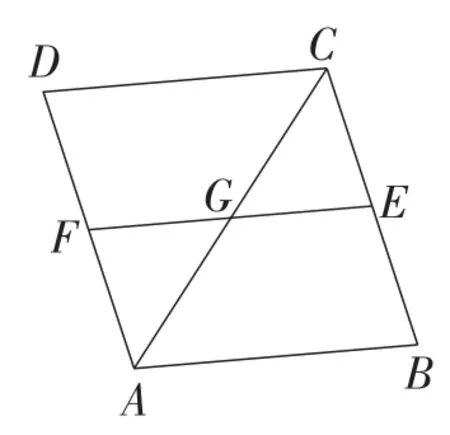
图7

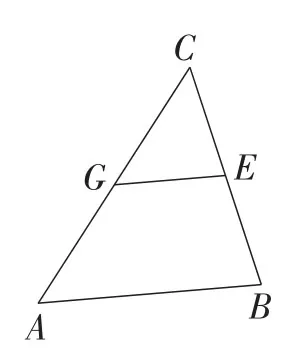
图8

去掉图7中▱ABCD的对角线AC左侧部分的图形，得到如图8所示的三角形，则GE是连接△ABC的两边AC，BC中点的线段，像这样，连接三角形两边中点所得到的线段叫做三角形的中位线.

探究：三角形的中位线有什么性质？

不难发现：三角形的中位线平行于第三边且等于第三边的一半.

然后，教师指导学生分析定理的证明思路，给出定理的证明过程.

这样，三角形中位线定理是在深化探索平行四边形对角线关系的活动中自然合理地发现的，这一发现过程也为学生提供了证明三角形的中位线定理的思路启发，把线段平行且倍分问题通过延长或截取，转化为证明线段之间的平行且相等问题，并进一步转化为与平行四边形相关的问题.这一探究过程，把三角形的中位线定理的发现、提出和证明过程融合到平行四边形的深化研究活动中，体现了探索平行四边形要研究其构成要素（边）和相关要素（对角线）的位置和数量关系.三角形的中位线定理是进一步研究平行四边形中过对角线中点和一边中点连线与边的位置和数量关系，是研究平行四边形的延伸.这样，既可以让学生经历自然合理的发现、提出、分析和解决问题的过程，又是几何图形研究一般套路的再次运用，有利于发展学生的数学探究发现和思考活动的经验.