基于ROS的工业机器人轨迹规划和仿真

李 浩，郑智贞，黄顺舟，杨富伟，刘泽宇

(1.中北大学 机械工程学院，太原 030051；2.上海航天设备制造总厂，上海 200245)

0 引言

随着自动化的普及与机器人技术的快速发展，以及企业对于生产效率的需求，给工业机器人的发展提供了良好环境，工业机器人应用较为广泛。由于工业机器人连杆结构的复杂性和多自由度的工作空间，使得高精度的轨迹规划成为了工业机器人技术中一个普遍遇到的难题[1-2]。轨迹规划的好坏关系到工业机器人控制系统的性能，在整个机器人控制系统设计中占比较大的比重。目前对于轨迹规划的研究多是应用机器人仿真平台来进行的，例如CARMEN、TeamBots等，这些机器人开发平台各有特点，但是功能较为单一；一些机械制图软件例如Solodworks，同样可以对工业机器人进行仿真，但是缺乏算法；一些机器人厂家开发的商用软件如KUKA公司的KUKASim，但是其兼容性很差。ROS是一款主要应用于机器人开发的开源操作系统，具有多种编程语言兼容、免费开源、跨平台等优点。

工业机器人轨迹规划可以使所要控制的机器人完成在笛卡尔坐标系和关节运动坐标系的运动轨迹，在笛卡尔空间中规划机器人末端执行器运行轨迹，在关节空间坐标系中得出关节运动参数关于时间的函数。文献[3]用D-H参数法建立串联机器人模型，运用五次插值算法在ROS中实现了仿真，但对加加速度这个对关节柔性冲击影响较大的参数没有进行分析；文献[4]运用改进的D-H算法和高阶多项式差值算法进行6轴工业机器人轨迹规划算法研究，并在Matlab中进行了仿真实验，但是仿真过程没有实际机器人模型且Matlab提供了算法API，无需进行底层算法编码工作；文献[5]提出了一种在ROS中构建模型的方法，包括外界三维模型导入及URDF文件编写。

本文通过将工业机器人实体模型转换为ROS中所使用的URDF格式文件，使用Moveit！工具添加在笛卡尔空间下的插值算法，生成轨迹规划所需要的配置文件，引入加加速度参数，并对S形曲线轨迹规划算法进行优化，将优化后的S形曲线轨迹规划算法植入ROS配置文件中，编写launch文件建立与Move_group节点的通讯。最后在Rviz中进行仿真实验，并运用ROS工具观察机器人关节角度的变化，可以看出机器人关节转动平滑，角度变化连续，能够有效的降低关节运动过程中产生的柔性冲击。

1 机器人模型建立

本文以ABB-IRB-4400机器人为研究对象，该机器人是6自由度串联工业机器人。由于ROS中采用的是机器人描述格式URDF(Unified Robot Description Format)来构建机器人，URDF使用XML标签来描述机器人的每个组件，以URDF形式先描述机器人基座(在URDF中将基座看作一个固定的连杆)的名称和类型、连接到基座的连杆，之后逐一说明连杆和关节的内容。连杆link标签描述连杆的名称、大小、重量和惯性等，在URDF中可以输入CAD文件用于可视化界面的模型显示，如STL和DAE。所以可以使用三维建模软件建立各个连杆的三维模型，然后通过link标签将模型导入，joint标签描述连杆之间的关节，包括关节的名称、类型、并且定义连接两杆的父子关系[6-7]。limit标签还可以设置关节运动的极限，例如给予关节的力，速度和角度等物理量的限制，还有很多标签用于描述机器人的一些其他特征，如颜色，材料等。

在完成URDF文件的编写后，还可以通过RViz3D可视化工具来验证文件的正确与否。如图1所示，RViz中显示的机器人模型正确。图2是用PROE建立的各个连杆的模型。

图1 RViz显示机器人

图2 机器人连杆模型图

2 笛卡尔空间轨迹规划

Moveit！是ROS中用于轨迹规划功能非常强大的工具，它具有非常多的功能，包括用于运动规划的快速逆运动学分析、运动学算法、动力学、运动规划和控制器。Moveit！中的核心节点Move_group可以使用ROS动作和服务与用户交换命令，可以从URDF文件和Moveit！配置文件中接受机器人信息，并且能够通过ROS话题和动作提供机器人的状态与控制，还可以提供环境信息[8]。

2.1 直线轨迹规划

机器人末端从初始点P1(X1,Y1,Z1)运动到P2(X2,Y2,Z2)，其运动轨迹为一条直线的情况。在笛卡尔空间的基坐标系下，用矢量方程表示出P1和P2：

P1=X1i+Y1j+Z1k

(1)

P2=X2i+Y2j+Z2k

(2)

用d表示这两点的直线距离，那么在机器人末端以速度矢量v从P1运动到P2这段时间T内，任意t时刻，机器人末端的位置矢量Pt(Xt,Yt,Zt)可以计算出：

(3)

在ROS中，通过RViz实现直线插补仿真，具体过程如下：首先给定P1和P2，由P1运动到P2，机器人的轨迹动态如图3所示，然后采用笛卡尔空间的轨迹约束，通过逆解运算得出6个关节的变化过程，通过rqt_plot插件可以绘制出关节变化曲线。如图4所示，定义连接基座与连杆1的关节为1，依此类推，定义关节2～6，关节2对应图中曲线2，关节3对应图中曲线3，后文如没有特别指出，则对应关系不变，图中横坐标为运行时间，单位是s，纵坐标为关节角度，采用弧度制。

图3 直线轨迹运动动态图

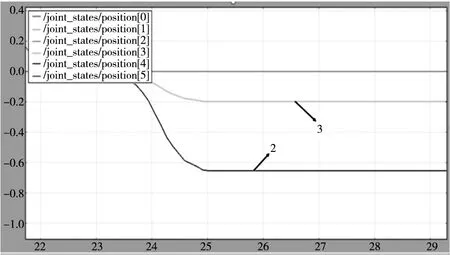
图4 关节角度变化曲线

2.2 圆弧轨迹规划

对于圆弧插补问题，首先要转化为二维平面问题，由不共线的三点A,B,C可以确定一个圆弧平面，其坐标分别为P1(X1,Y1,Z1),P2(X2,Y2,Z2),P3(X3,Y3,Z3)，那么A,B,C三点可以唯一确定一个过此三点的平面，通过对AB,BC分别做垂直平分线，两条垂直平分线相交于圆弧圆心处，可求得圆弧半径R，进而可以求出AB和BC两段圆弧的圆心角φ1和φ2，接着构建圆弧平面坐标系，也就是将OR(X0,Y0,Z0)坐标系原点与圆心重合，ORXRYR平面为圆弧所在平面，且保持ZR为外法线方向，如图5所示[2]。

图5 圆弧坐标系建立

令TR表示由圆弧坐标ORXRYRZR至基础坐标系的转换矩阵。若ZR轴与基础坐标系ZO轴的夹角为α，XR轴与基础坐标系XO轴的夹角为θ，由于运动是相对固定坐标系，通过绕Z轴和X轴旋转可得转换矩阵：

TR=T(XOR,YOR,ZOR)L(Z,θ)L(X,α)=

(4)

其中，XOR,YOR,ZOR是圆弧坐标系原点在基座标系下的坐标，L表示绕坐标轴旋转一定的角度。

在任意t时间内，基座标系下的坐标值为POt(XOt,YOt,ZOt)，圆弧坐标系下的坐标为PRt(XRt,YRt,ZRt)。

则在其插补周期内对应的圆心角为：Δφ=vt/R。

圆弧插补的总步数：N=φ1+φ2/Δφ+1。

可得第i个插补点Pi的位置坐标为：

(5)

通过转换矩阵运算可得圆弧位置插补为：

(6)

依照关节空间轨迹规划的方法，结合末端执行器空间的姿态欧拉角，可求得机器人末端执行器在各个插补点的位姿角。在ROS中实现的圆弧插补仿真如图6所示，通过rqt_plot插件绘制出的关节角度变化曲线如图7所示，圆弧轨迹规划中，6个关节角度均出现变化，从图中可以看出，关节变化平滑，万向节无锁死。

图6 圆弧轨迹运动动态图

图7 关节角度变化曲线

3 关节空间轨迹规划

工业机器人在运动过程中关节运动参数的变化对运动路径精度影响很大，通常在关节伺服电机进行启动或停止的加减速期间易产生突变，故引入加加速度参数，通过对S形轨迹规划方法优化，得到关节速度、加速度和加加速度的表达式，来完成对关节空间轨迹规划插值计算，保证运动轨迹的平滑性，避免了运动过程中产生的柔性冲击。

S形轨迹规划方法中关节运动的角速度变化可以描述为：

(7)

其速度和加速度曲线如图8所示，可以看出，加速度的变化呈梯字型，所以导致其导数加加速度在拐点处存在突变，在运动过程中造成柔性冲击。针对关节运动过程中加加速度的非连续性，可以采用三角函数代替梯形函数对其进行拟合优化。

图8 速度加速度变化曲线图

在运动过程中，速度和加速度连续变化的同时，采用正弦函数对加速度曲线进行拟合，从而消除加加速度在变化过程中产生的突变，可以有效的避免由于突变产生的振动和冲击，从而避免影响机器人运行轨迹的精度。用A表示加速度的峰值，w为角频率，T为运动总时长，Ta表示关节运动中加速过程的时间，得出加加速度表达式为：

(8)

通过积分运算可以得到加速度的正弦函数表达式：

(9)

再次进行积分运算可以得到速度的表达式如下：

(10)

通过对优化后的速度，加速度，加加速度的表达式曲线绘制，可以看出在加速或减速的Ta期间，关节速度和加速度变化连续平滑，通过具有光滑性的三角函数拟合，加加速度的变化相对之前表现为缓慢递增或者递减，变化更加均匀连续。

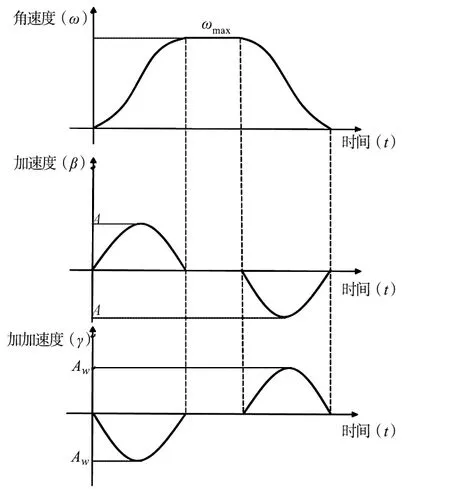
图9 优化后的变化曲线

设关节运动在t=0和t=T时刻角度值分别为θ0和θ1，且速度和加速度均为0，结合伺服电机加速度幅值A，可以得出Ta为：

(11)

综合上述公式，可以得出插补点的表达式为：

(12)

在ROS中实现关节空间轨迹规划的具体过程：通过Moveit！生成相关配置文件后，此时通过RViz仿真器可以接受运动指令，控制机器人运动并对其关节位置信息进行反馈。接着使用Python语言编译插值算法，使其作为一个单独的action文件启动，并且建立于RViz节点的通信。运行此action文件后，RViz便可接受节点信息并作出响应。关节空间轨迹规划ROS仿真如图10所示。

图10 关节空间轨迹规划

4 结束语

本文通过ROS机器人平台对六轴工业机器人进行路径规划算法研究和仿真实验，完成了在笛卡尔空间的直线轨迹和圆弧轨迹的模型构建，并用RVIZ进行了仿真；引入了加加速度参数，通过优化的S型轨迹规划方法得到的关节角速度、加速度和加加速度光滑连续，减少了关节运动过程中的柔性冲击，保证在关节运动的平稳性及运动轨迹的平滑性，并且对机器人末端轨迹进行了仿真，验证了该算法的正确性。对ROS机械臂开发和工业机器人路径规划研究都有一定的指导意义。