成拱工况下仓壁超压弹性波动态模拟分析

冯 永，原子然，张盼盼，谢飞亚，李晓一，李 萌

（河南工业大学土木建筑学院，河南郑州 450000）

近年来，卸粮成拱对仓壁造成破坏的现象时有发生，但现有室内实验及理论计算模型无法客观反映筒仓卸粮成拱下的仓壁超压机制形成过程。为了适应粮食行业的迅速发展，深入研究仓壁侧压力势在必行。

国内外学者提出了理论计算公式量化筒仓仓壁压力，如Jassen公式，但并不适用于卸粮工况，更不适用于成拱工况[1-10]。部分学者研究了成拱时侧壁产生的超压，发现物料含水率、物料的内外摩擦系数、料仓尺寸等均会影响卸料成拱[11-14]。卸料过程中的成拱现象会导致侧壁超压[15]，拱内颗粒承受仓中粒料的大部分应力。实际工程中，仓壁并不是绝对刚性的，仓壁弹性变形传播在卸料过程中影响仓壁动压力的形成[16-18]，但是超压形成的细观机制尚不明确。

在卸粮成拱这一工况中，研究仓壁压力弹性波分布规律对于揭示仓壁超压作用机理具有重要借鉴意义。本文中，通过工程实例建立缩尺模型，运用室内实验和PFC软件对筒仓卸料过程进行动态模拟，揭示筒仓卸粮成拱工况下超压弹性波的形成对仓壁超压影响，分析二次超压的形成和传播机制，为预防类似事故提供理论依据。

1 形成机理

1.1 成拱实现过程

粮食是一种散粒体，散粒体兼具液体和固体的一部分特性，但是其物理力学特性与固体液体又都不尽相同。从细观的角度来看，散体的本质是很多离散颗粒的集合，在一定范围内呈现出与液体相类似的流动性，从整体上来看依然可以认为贮料是各向同性的散粒集合体。

贮料在静态工况下是不可能成拱的，成拱的过程其实是一个动态平衡的过程。在卸料过程中，仓内颗粒在自重作用下开始下泻，同时，颗粒之间以及颗粒和仓壁之间的摩擦挤压碰撞等耦合作用使得颗粒下泻呈现复杂的运动状态，颗粒的位置和速度以及所受到的合力和合力矩每时每刻都在变化。各颗粒之间的相互移动和摩擦挤压会使颗粒通过位置和应力状态的不断调整找到一个可以互相传递压力的最佳位置，形成连接仓壁两侧的完整力链，且力链之间不产生颗粒的空位，以实现力向拱脚的传递和对上部物料流动的阻碍，并要求拱脚有足够的强度用于支撑。由于力链的形成影响了颗粒的正常出流，因此颗粒流动速度的降低产生与颗粒流速方向一致的惯性力，筒仓内拱形力链以上的颗粒自重以及新产生的惯性力全部作用于颗粒拱，并通过拱脚传递到仓壁两侧，使得拱脚处仓壁产生超压。

1.2 超压弹性波形成机理

在实际工程和数值模拟中，仓壁都不是理想的绝对刚性体，仓壁具有一定的弹性，拱脚处的超压会使紧贴拱脚的仓壁产生微小的横向膨胀变形，且超压会造成储料密度增大，膨胀段容积的增大和储料挤密造成的粮食体积缩小会容纳更多的贮料，流入的储料也具有一定速度，在流入膨胀区段后必然伴随速度降低为零的过程和随之产生的惯性力。仓壁膨胀示意图如图1所示，随着贮料的不断流入扩张体积中，成拱超压自下而上以波的形式在仓壁上传播。

图1 仓壁膨胀示意图Fig.1 Diagram of silo wall expansion

2 工程实验相似性认证

根据工程实例[11]建立实验模型，实验与模拟均采用20∶1缩尺模型，参与卸粮成拱过程的主要物理参数有重力加速度g、粮食密度ρ、筒仓模型几何尺寸L、墙体弹性模量E、粮食黏聚力C、粮食内部的摩擦力φ1、粮食外部的摩擦力φ2、仓壁受到的应力为σ。其一般函数式为

通过相似性准则可以得到函数表达式

几何相似性系数CL为1/20；因为密度和重力加速度难以在实验中改变，所以采用密度相似系数Cρ=1、重力加速度相似系数Cg=1。根据Jassen公式估算应力相似性系数，并带入式（2）中相似性准则验证，可以认证本文中模型试验的材料相似性、几何相似性与应力相似性之间相互满足，从而证明所采用的缩尺模型满足相似性认证。

3 实验研究

3.1 实验模型及压力波监测

该工程实例中破坏仓的内径为Φ6 000 mm，仓壁厚160 mm，仓壁高度为20 000 mm，卸料口大小为Φ1 000 mm。成拱实验模型结构示意图如图2所示。

图2 成拱实验模型结构示意图Fig.2 Schematic diagram of arch-forming experimental model

成拱实验所用20∶1的缩尺模型尺寸如表1所示。

表1 成拱实验模型尺寸Tab.1 Size of the arch model

筒仓用厚度为8 mm的亚力克材料制作，以期清楚地观测到颗粒的流动状态。将实验模型仓内装满粒径为5～6 mm的小麦，待装料完成后撤掉料斗底板进行卸粮实验，通过添加粉尘、改变含水率、仓壁贴砂纸等方法，进行多次实验，最后实现筒仓卸粮成拱，成拱实验系统如图3所示。

图3 成拱实验系统Fig.3 Experimental system of arched grain

在筒仓左侧仓壁布置10个监测点，每个监测点上安放一个应变片来监测仓壁侧压力，可以得到仓壁侧压力在成拱过程中的变化图像，仓壁监测点分布如图4所示。

图4 仓壁监测点分布图Fig.4 Distribution of monitoring points on silo wall

3.2 实验结果分析

实验发现，成拱现象大致发生在筒仓的1/3高度处，1/3高度以下的颗粒自由卸料，而筒仓上部在卸料过程很快迎来了零压力区，取0.1 m2墙段只绘制编号为 4、5、6、7、8 这 5 个监测点侧压力图线，各监测点处侧压力如图5所示，可以看到，成拱过程中侧壁成拱压力的形成过程。伴随着卸粮成拱，仓侧压力波动，并在波峰出现稳定侧压，即为成拱压力，但受限于客观实验条件不能精确观测仓侧成拱压力形成的细观机理，因而在后文中通过PFC仿真模拟研究。

图5 仓壁监测点处侧压力Fig.5 Pressure at monitoring points

4 数值分析模型

4.1 线性接触模型与本构模型

4.1.1 线性接触模型

球与球之间以及球与墙面之间的接触都采用线性接触模型。线性接触规定了两物体之间无穷小的交界面是不能抵抗弯矩的，接触弯矩常等于0。线性接触中由线性元件和阻尼元件来提供接触力，线性元件提供无张力的线弹性力和摩擦力，而阻尼元件提供2个单元体之间的粘结力，将线性元件基本等同于一个弹簧和滑移板，将阻尼元件等同于一个阻尼器，线性接触模型如图6所示。

图6 线性接触模型Fig.6 Linear contact model

4.1.2 本构模型

1）颗粒与颗粒

根据力-位移定律，得到2个颗粒接触时的单位矢量模型和颗粒接触变形的情况。2个粮食颗粒i、j相互接触的示意如图7所示，设2个颗粒中心坐标分别为（xi，yi）、（xj，yj），因为小麦颗粒的粒径分布虽然不同，但是差异不大，可以认为2个颗粒半径均为 rc，接触点处的法向向量n→=（nx，ny），切向向量为t→=（tx，ty）。

图7 粮食颗粒接触示意图Fig.7 Schematic diagram of contact between grain particles

由此可以得接触点处的法向和切向向量的表达式为

而颗粒i、j接触点的速度分别表示为

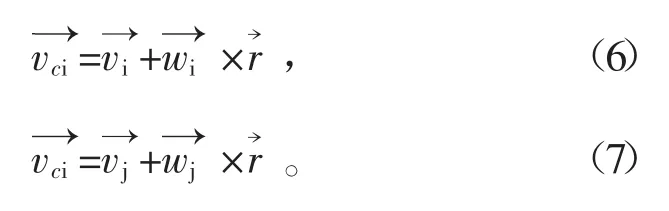
将式（6）、（7）带入式（5），可得到

相对速度在法向和切向的分量为

对于颗粒i、j，法向切向的速度分量都造成了相应方向的位移，根据上述方式所计算出的速度分量，可以得到一个时间段变化的位移分量的表达式为

根据力-位移定律可以得到力位移关系的表达式为

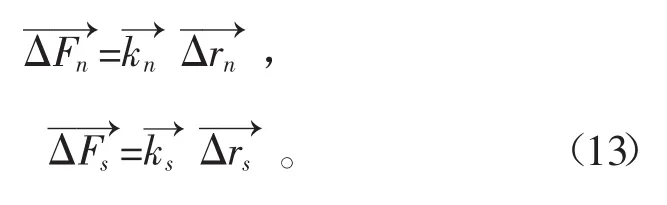
由此易得颗粒i的运动方程为

式中I为颗粒的惯性矩，在线性接触模型中一般认为颗粒接触点的弯矩常等于零。

在运算的每个微小时段，细观参数都在发生改变。以颗粒i为例，力在一个微小时段的更新为

速度在一个微小时段的更新为

颗粒位置在一个微小时段的更新为

2）颗粒与墙体

颗粒与墙体的接触示意图如图8所示。设代号为i的颗粒中心点坐标为（xi，yi），代号j的墙体围绕点（xj，yj）发生旋转。墙壁与颗粒接触点坐标为（xc，yc）。接触点处的法向向量=（nx，ny），切向向量为=（tx，ty）。

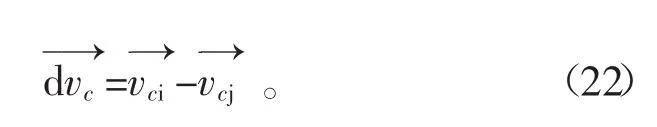
图8 颗粒与墙体接触示意图Fig.8 Schematic diagram of contact between particle and wall

而颗粒i与墙体j在接触点的速度分别为

式中，假定墙体不发生平动，所以vj=0为球体的半径向量，为墙体转动的半径向量，wj为墙体转动角速度。

将式（23）、（24）带入式（22），可以得到接触点处的相对移动速度

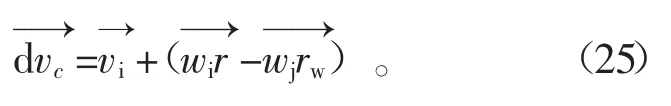
相对速度在法向和切向的分量为

接触力法向切向的增量及位置速度和力的更新方法均依前文所述，不再赘述。

4.2 数值模型的建立

参照模型实验建造同样是20∶1的缩尺模型，根据文献[12]所提供的粮食力学特性数据，并参照上文所述的相似条件，选取利于成拱的颗粒和墙壁的力学参数，如表2所示。Wall和Ball分别表示墙体单元和颗粒单元，kn、ks则分别为它们的法向和切向刚度。

表2 模拟中颗粒和墙壁力学参数Tab.2 Mechanical parameters of particle and wall in simulation

墙体和颗粒的线性接触模型所选取的参数如表3所示。

表3 模拟中接触模型的主要参数Tab.3 Main parameters of the contact model in simuloction

在PFC模型中，仓壁由分段建立的20个Wall单元组成，分别代表20个虚拟监测点监测成拱工况下仓壁动态侧压力。分层装料完成并达到的稳定装载模型如图9所示。

图9 稳定装载模型Fig.9 Steady loading model

4.3 动态监测点的布置

颗粒在筒仓卸粮成拱的过程中呈现复杂的，属于非对称、非均匀的流动状态。参照上述试验模型沿左右仓壁各生成10段100 mm的墙体，代表设置10个虚拟监测点以监测卸粮过程中仓壁压力分布变化，仿真模拟中的监测点布置如图10所示。

图10 仿真模拟中的监测点布置Fig.10 Aarrangement of monitoring points in simulation

5 数值模拟分析与结果

通过采用有利于成拱的物理力学参数进行多次模拟试验，最终实现成拱。对自重装料并达到稳定后进行的卸料过程进行动态模拟分析，卸粮成拱时的颗粒分布图如图11所示。

图11 卸粮成拱时的颗粒分布图Fig.11 Distribution of particles when grain is arched

5.1 力链形成过程

在卸料过程中，颗粒的速度位置和应力不断发生变化，逐渐在筒仓内形成一个连接仓壁两侧的不规则拱形力链。如果颗粒之间可以很好地传递应力而且拱脚拥有足够的强度，就会出现卸粮成拱现象，阻碍了拱形上方粒料的出流。成拱过程中的力链变化如图12所示。

图12 成拱过程中力链变化Fig.12 Force chain formation process

5.2 超压弹性波形成的模拟分析

筒仓成拱的拱脚位置大约在距离筒仓和料斗交界约1/3处，因此在3号监测点以上位置的侧压力受到筒仓成拱超压的影响，而1、2、3号监测点的侧压力变化均未受到成拱的影响；又因为成拱时已经卸出一部分颗粒，仓壁出现零压力区，所以选取4、5、6、7、8共5个监测点进行观察和分析。

PFC软件可以直接绘制出仓壁侧压力随时步变化的图像，但是无法精确看到每一时步所对应的侧压力数值，所以直接使用PFC输出每一时步各点对应侧压力的Excel表格，并绘制出动态侧压力的折线图。

左侧仓壁各监测点的动态侧压力如图13所示。仓壁成拱左侧压力分布如图14所示，成拱超压系数如表4所示。

图13 左侧仓壁动态侧压力Fig.13 Ddynamic pressure at each monitoring points on left side of arch

图14 仓壁成拱左侧压力分布图Fig.14 Pressure distribution on left side of arch

表4 左侧仓壁各监测点侧压力超压系数Tab.4 Overpressure coefficient at each monitoring point on left side of arch

仿真模拟中，右侧仓壁各监测点的动态侧压力如图15所示。

图15 右侧仓壁动态侧压力Fig.15 Dynamic pressure at each monitoring points on right side of arch

仓壁成拱右侧压力分布如图16所示，成拱超压系数如表5所示。可以清晰地看到，仓壁侧压力的分布随着深度的增加持续增大，而成拱时的超压系数也随深度而增加，且成拱时侧压力的超压并不出现在同一时间点，这应该与在拱形上方由下而上速度降低的先后顺序有关，也与成拱后仓壁由拱脚部分自下而上以弹性波的形式传播超压的行为有关。

图16 仓壁成拱右侧压力分布图Fig.16 Pressure distribution on right side of arch

表5 右侧仓壁各监测点侧压力超压系数Tab.5 Overpressure coefficient at each monitoring point on right side of arch

对比图5、13、15可以发现，侧压力随卸料时间变化的趋势与室内试验结果相符合，实验中成拱侧压力的大小与模拟结果相差不大，由此可以证明PFC模拟的精确性。

5.3 超压弹性波传播规律的模拟分析

模拟中，成拱超压时左侧仓壁各监测点时步如图17所示。

图17 成拱超压时左侧仓壁各监测点出现的时步Fig.17 Time step of arched overpressure occurrence at monitoring points on left side of arch

模拟得到的成拱超压时右侧仓壁各监测点步如图18所示。

图18 成拱超压时右侧仓壁各监测点的时步Fig.18 Time step of arched overpressure occurrence at monitoring points on right side of arch

鉴于筒仓结构的对称性，多数学者都认为筒仓细观参数的分布也应该是对称的，但是实际工程中，筒仓中的颗粒流态复杂，呈现非均匀性和非对称性，超压弹性波的出现和传播以及仓壁超压的大小也有微小的差别。以左侧仓壁为例，由图17可见，各监测点超压的出现有先后顺序，4号监测点的仓壁超压波峰出现最早，在模拟迭代105 750步时出现稳定的成拱超压，随着时间推移，4、5、6、7、8 号监测点位置的仓壁侧压力波动的波峰依次出现，8号监测点超压波峰出现最晚，在迭代106 510步时才出现稳定的成拱超压。且由图18可见，虽然右侧仓壁弹性波出现的时步与左侧仓壁有微小的差别，但在侧壁各深度下超压波动的传播依然几乎是均匀的。

6 结论

通过室内实验及PFC动态模拟，得出以下结论：

1）卸粮成拱时仓壁出现超压，导致超压的原因主要是拱阻碍颗粒出流颗粒速度降低所产生的惯性力。

2）观察卸粮成拱时仓壁侧压力的波动图像可以发现，超压波峰随着深度的增加先后出现，说明超压从拱脚处开始，在仓壁上以波的形式向上传播，颗粒速度的降低过程也是逐渐向上扩散的。

3）随着筒仓高度的增加，卸粮成拱时仓壁的侧压力降低，超压的增量减小，且在筒仓的各深度处超压系数也随深度增加而增大。

4）在筒仓各深度处，出现波峰的时间间隔比较均匀，可以认为超压波动的传播也是匀速的。

研究成果揭示了筒仓成拱工况下仓壁超压的形成机理，相关结论可为筒仓安全性设计提供参考。