一种非等距网格差分格式求解含双边界层的反应扩散问题

杜金月，王彩华，张文逸

（天津师范大学 数学科学学院，天津300387）

奇异扰动问题是指微分方程中的高阶导数项含有一个小参数，奇异扰动问题广泛应用于流体力学、化学反应现象、控制论以及电子场等领域[1-3].传统数值方法求解此类问题常会因发生数值振荡而失效，因此寻找适应小参数的数值方法尤为重要.此类问题通常有2种处理方法.一种是从数值格式构造的角度出发，如：文献[4-5]针对一维定常对流扩散反应方程，基于截断误差余项修正思想，分别构造了一种混合型紧致差分格式和一种高精度紧致差分格式；文献[6]通过对微分方程系数常数化处理和基于余项修正思想，给出了对流扩散方程的指数型高精度紧致差分格式；文献[7]延用文献[6]的思想，给出了变系数对流扩散反应方程的指数型差分格式.另一种思路是从网格适应剖分角度出发，如：文献[8]基于非均匀网格的泰勒展开，通过一阶二阶导数的高阶中心差分格式，得到对流扩散反应方程的非等距的差分格式；文献[9]给出对流扩散方程的一种非等距差分格式，并结合了几种不同的非等距网格剖分方法，虽然该方法在等距情形下仅有二阶精度，但数值实验表明其求解小边界层问题的效果较好.

文献[10]针对对流反应扩散方程，在基本差分格式的系数上添加拟合因子，数值实验表明，相比无拟合因子（拟合因子为1）的格式，结果精度得到显著提高.但该方法是在等距网格下Dahlquist差分格式的基础上引入拟合因子，因此导致数值解误差分布不匀，在边界层附近的误差相对较大.本文对该方法进行改进.首先在较粗的等距节点上采用含拟合因子的Dahlquist差分格式，初步得到一组数值估计解；然后选择其中2个内节点（分别靠近左右边界层）将区间剖分为3个区域，在边界层区域采用含有拟合因子的差分格式再次计算，而在中间解平滑的区域使用二阶中心差分格式.数值实验表明本文方法比文献[10]的方法计算效果更好，尤其更有利于观察双边界层附近的数值解.

1 二阶奇异扰动反应扩散问题

考虑反应扩散两点边值问题

扩散量u定义在有限区间I=（a，b）上，边界条件为

其中c（x）、f（x）满足一定的光滑性条件使问题的解存在唯一.为方便，设c（x）≥c＞0，这个条件限定了问题的边界层出现在端点两侧.

考虑问题（1）～（2）的解的渐近展开式

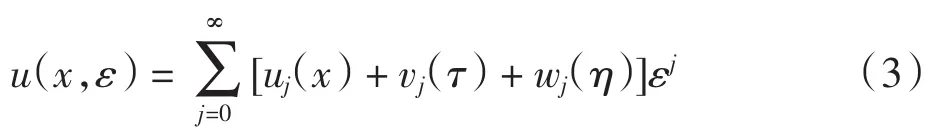
其中

式（5）为关于问题（1）的退化解（即小参数ε为0时的解）.称v0（x）为左边界层校正解，w0（x）为右边界层校正解，设其满足下列常微分方程

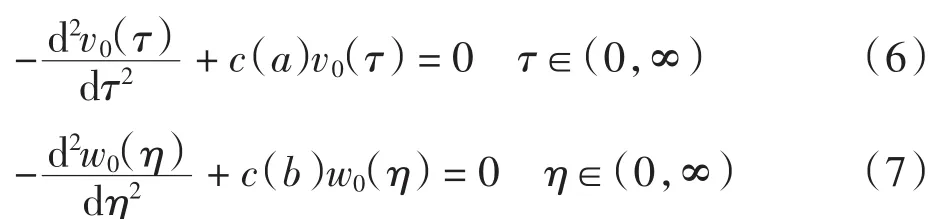
边界条件为

求解方程（6）～（10）， 得v（0τ）和w（0η），代入式（4）得

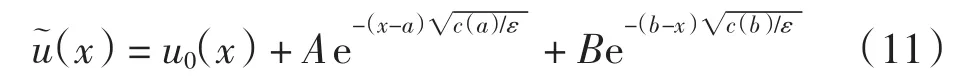
其中

将区间[a，b]等分成m份（m为整数且为4的倍数），节点记为 a=x0，x1，x2，…，xm=b，网格步长h=（b-a）/m.记 u（x）i为微分方程（1）～（2）在节点的精确值，Ui为设计的数值方法得到的近似解，c（x）i、（fx）i简记为 ci、fi.

在节点x=xi处改写方程（1）

其中g（xi）=（fxi）-c（xi）u（xi）.因为

将式（15）和式（16）代入式（14），并去掉二阶截断误差，整理得

记式（17）为差分格式FD1.

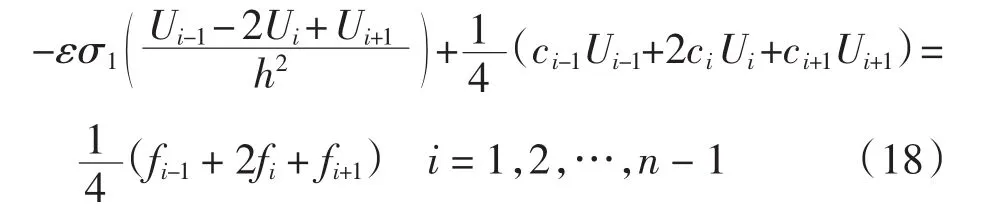
为确定拟合因子σ1，考虑式（1）右端为齐次的情况，即令（fx）≡0，则式（4）中u（0x）=0，且令右边界层校正解w（0η）=0，则有

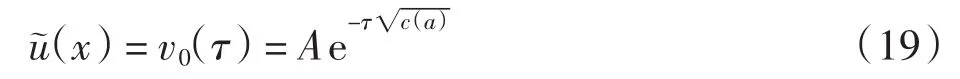
令

其中A由式（12）确定.分别将 Ui-1、 Ui、 Ui+1代入式（18），因右端齐次时有式（18）中fi≡0，且左边界点处的函数值已知，考虑边界层附近h→0，则可得到

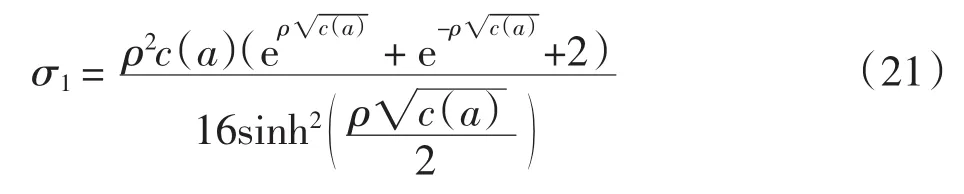
σ2为常数.

将拟合因子 σk，k=1、2代入式（18），整理得

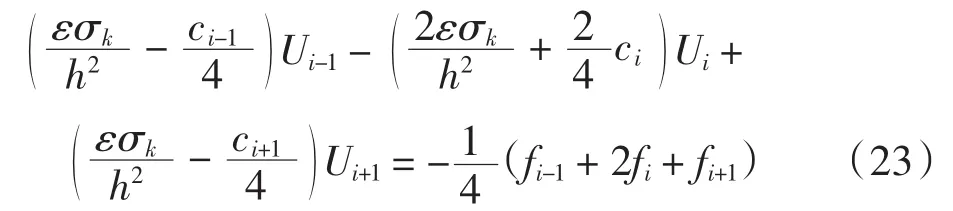
为简洁，将上式改写为

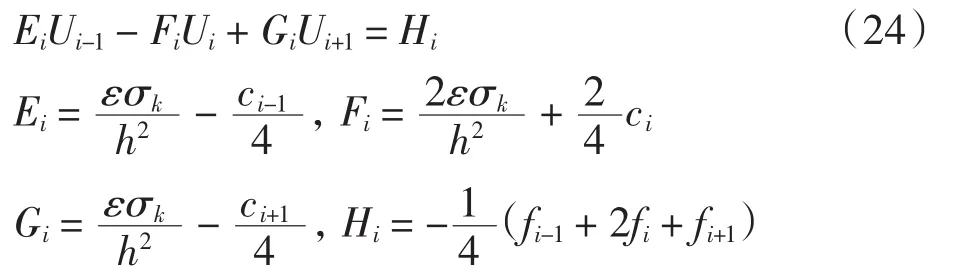
式（24）～式（26）为带拟合因子的差分格式，其系数矩阵为三对角矩阵，可采用追赶法求解.以下记该等距差分格式为FD2.

对于等距节点的粗剖分，利用差分格式FD2可得到一组数值预测解.然后选择其中2个内节点a+，将区间剖分为3个区域：左边界层区域，解平稳的中间区域和右边界层区域，如图1所示.

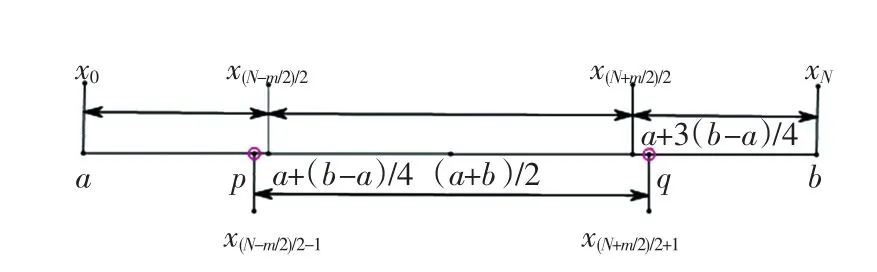
图1 区间剖分示意图Fig.1 Diagram of interval partition

在两边界层区域布置更多的网格节点，而在中间区域采用较粗的网格.在边界层区域仍采用含有拟合因子的差分格式再次计算，而在中间解平滑的区域，利用二阶中心差分格式.为提高计算精度，中间区域可进一步扩大到（p，q）， 使得（p，q），边界p、q处的解值可由前面两边界层区域内的计算值确定.记此时的非等距差分格式为FD3，具体算法如下：

算法1

步骤1等距差分格式FD2.

先将图1区间[a，b]等分成m份（m为整数，且为4的倍数），， 在区间应用差分格式（24）～（25）求出.在区间应用差分格式（24）和（26）求出.综上得到一组.

步骤2非等距差分格式FD3.

先记N为区间[a，b]的非等距剖分的份数，N＞m，且为偶数.

步骤2.1如图1将区间[a，b]分成3个区域，分别 为和.

步骤2.2将左区域细化剖分为等份，其中步长为，应用差分格式（24）（k=1），得到 Ui，i=0，1，2，…，（N-m/2）/2，其中该区域左边界条件为U0=u（a）=α，右边界条件为.

步骤2.3将右区域细化剖分为等份，其中步长为，应用差分格式（24）（k=2），得到 Ui，i=（N+m/2）/2，（N+m/2）/2+1，…，N，其中该区域左边界条件为，右边界条件为 UN=u（b）= β.

步骤2.4将中间区域扩展为[p，q]，取

将区间[p，q]剖分为m/2+2份，步长为

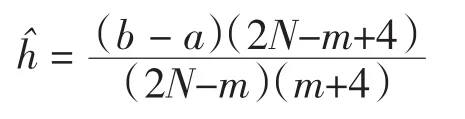
应用二阶中心差分格式，得到Ui，i=（N-m/2）/2-1，（N-m/2）/2，…，（N+m/2）/2+1，其中该区间的边界条件为 u（p） =U(N-m/2)/2-1，u（q） =U(N+m/2)/2+1.

综上得到 Ui，i=0，1，2，…，N.

2 数值实验

例1考虑一般二阶反应扩散方程的边值问题

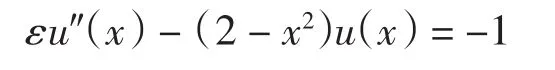
x∈（-1，1），边界条件为 u（-1）=0，u（1）=0，该问题的精确解为

表1给出了当ε=10-6时例1在不同等距网格剖分下差分格式FD1和FD2的最大误差（Err）和收敛阶（r）的比较.由表1可见含拟合因子的差分格式FD2的计算精度明显优于FD1，且FD2有比较稳定的二阶收敛性.

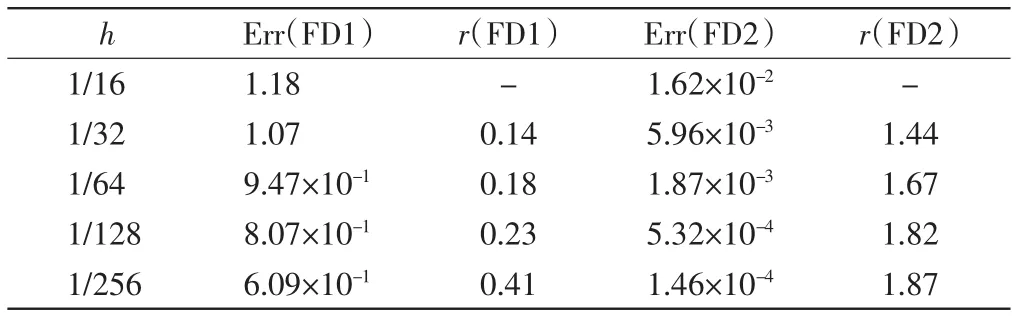
表1 当ε=10-6时，例1采用FD1和FD2的最大误差和收敛阶Tab.1 Maximum absolute errors and convergence rates of FD1 and FD2 for example 1 when ε=10-6

在格式FD2中，m取200，计算不同ε下的最大误差.执行算法1，在步骤1中m取为80，得到一组预测值，步骤2中N取为200，得到非等距情形下FD3的差分解，计算不同ε下的最大误差.以上结果见表2.由表2可见，在剖分总节点数相同的情况下，FD3的计算精度有所提高，因为在边界层处加密了节点，所以与等距情形相比，FD3更有利于观察解在边界层的变化.

表2 ε取不同值时，例1采用FD2和FD3的最大误差Tab.2 Maximum absolute errors of FD2 and FD3 for example 1 with different values of ε

图2给出了当ε=10-6时例1采用3种差分格式的误差曲线，可以看到中心差分格式在边界层误差比较大.

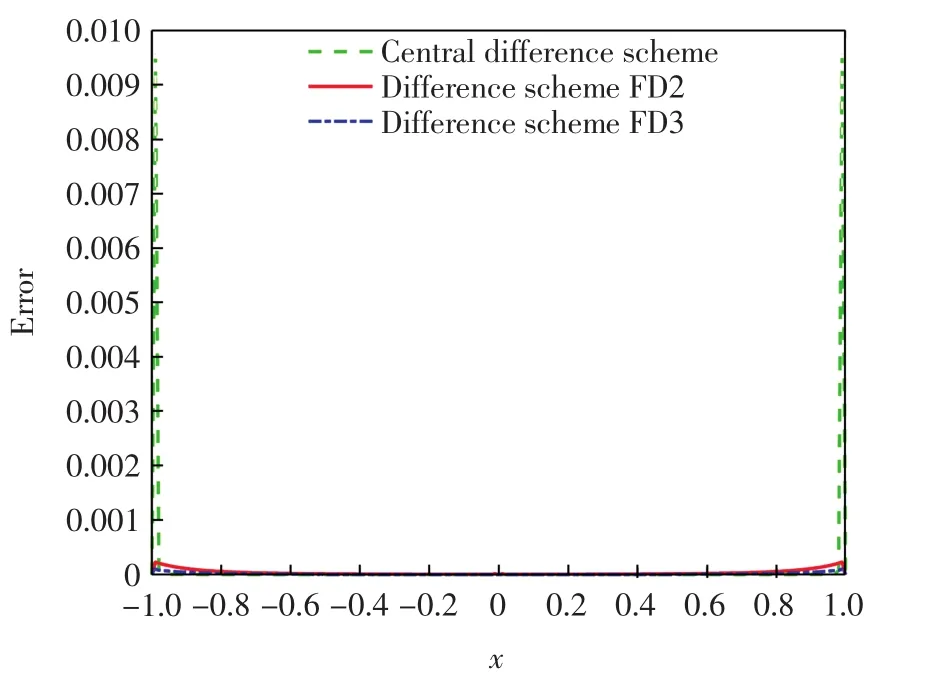
图2 当ε=10-6时，例1采用3种差分格式的误差曲线Fig.2 Curves of errors of three difference schemes for example 1 when ε=10-6

单独将差分格式FD2与差分格式FD3的误差曲线进行比较，见图3.

图3 当ε=10-6时，例1采用FD2和FD3的误差曲线Fig.3 Curves of errors of FD2 and FD3 for example 1 when ε=10-6

由图3可见，差分格式FD3在边界层的误差明显小于FD2的误差，这说明非等距剖分的计算效果优于等距剖分.

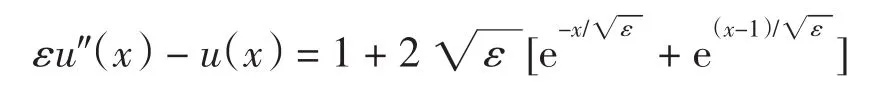
例2考虑一般二阶反应扩散方程的边值问题x∈（0，1），边界条件为 u（0）=0，u（1）=0，该问题的精确解为

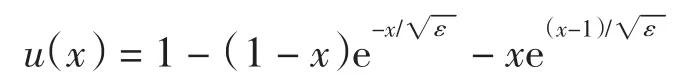
表3给出了当ε=10-3时例2在不同等距网格剖分下差分格式FD1和FD2的最大误差和收敛阶的比较，可见FD2的计算效果明显优于FD1，为比较稳定的二阶收敛.

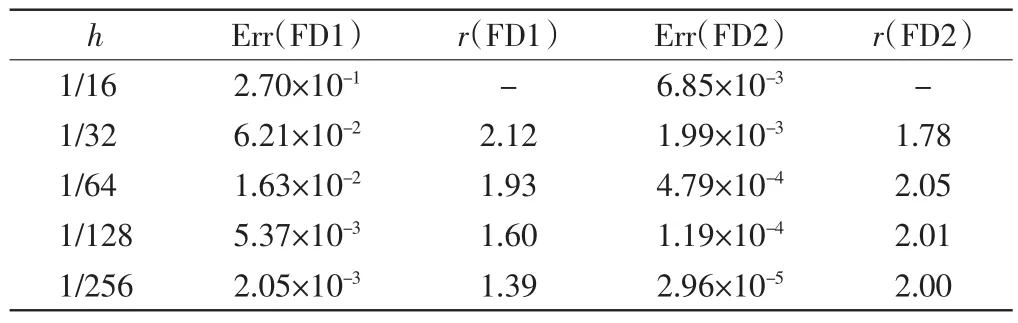
表3 当ε=10-3时，例2采用FD1和FD2的最大误差和收敛阶Tab.3 Maximum absolute errors and convergence rates of FD1 and FD2 for example 2 when ε=10-3

计算不同ε下FD2和FD3的最大误差，结果见表4，其中剖分方法同表2.图4给出了当ε=10-3时例2采用3种差分格式的误差曲线.由表4和图4可见，非等距网格差分格式FD3的计算效果明显优于另2种格式.

表4 ε取不同值时，例2采用FD2和FD3的最大误差Tab.4 Maximum absolute errors of FD2 and FD3 for example 2 with different values of ε

图4 当ε=10-3时，例2采用3种差分格式的误差曲线Fig.4 Curves of errors of three difference schemes for example 2 when ε=10-3

3 结语

本文针对含双边界层的微分方程问题，将区间剖分为3部分，左右边界层采用含拟合因子的差分格式，给出了一种非等距差分格式.由数值实验结果可以看出，在相同份数的剖分下，非等距差分方法FD3的数值结果优于等距差分方法FD2，由误差曲线也可以明显看出FD3在边界层附近的误差较FD2明显减小.

本文是在二阶差分格式的基础上引入了拟合因子，接下来可考虑在更高阶的差分格式上引入拟合因子，以进一步提高数值解的精度.