Wiener指数,Hyper-Wiener指数与泛圈图
舒阿秀,王礼想,夏祥伟
(安庆师范大学数学与计算科学学院,安徽安庆246133)
设G=(V,E)为n阶简单连通图,其顶点集V=V(G)={v1,v2,…,vn},边集E=E(G)为V的二元重集构成的集合[1]。 称E中元素{u,v}(u≠v)为G的边,边{u,v}简记为uv。记为G的补图,其顶点集V(=V(G),边集E()为把G中所有不相邻顶点对连接起来得到的边的集合。顶点v的度dG(v)是指G中与v关联的边数,G的最小度记为δ(G)。G中vi到vj的最短路的长度,定义为vi与vj之间的距离,记作dG(vi,vj)。 如果图G的每个顶点的度均为n-1,则称G为完全图,记作Kn。如果图G=(V,E)的顶点集V可以被划分为互不相交的子集X和Y,使得V=X∪Y且任意边e={u,v}均满足u∈X,v∈Y或u∈Y,v∈X,则称G为二部图,可记作G=(X,Y;E)。 若|X|=p,|Y|=q,并且X中所有顶点与Y中所有顶点都相邻,则称G=(X,Y;E)为完全二部图,记作 Kp,q。 设 G1=(V1,E1)与 G2=(V2,E2)是两个顶点不交的简单图,它们的并图为G1∪G2=(V1∪V2,E1∪E2),又记为G1+G2;若G1=…=Gk,则用kG1来表示G1∪…∪Gk;它们的联图为G1∨G2=((G1)c∪(G2)c)c,即在 G1∪G2中添加由 G1中每个顶点到G2中每个顶点的边所得的图。若对每一个k(3≤k≤n),都含有长度为k的圈Ck,则称G为泛圈图。
图G的Wiener指数是与分子化合物的物理性质、化学性质相关性很高的拓扑指数,由Wiener于1947年在文献[2]中首先提出,记为W(G),被定义为G中任意两个顶点的距离之和,即

图G的hyper-Wiener指数作为Wiener指数的推广,记为WW(G ),是Randić于1993年在文献[3]中首先提出的,并给出了无圈图hyper-Wiener的定义,1995年,Klein等将hyper-Wiener的定义延伸到了所有的连通图中[4],
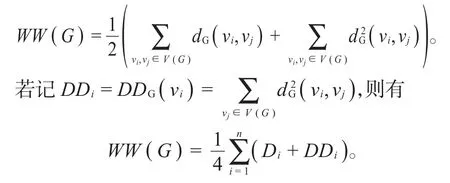
对含圈图的研究一直是图论中热点研究领域之一,例如文献[5]给出了一类图是X-可圈的充分条件。关于泛圈图,Bondy在文献[6]中利用任意一对不相邻顶点度之和的界给出泛圈图的一个充分条件;朱五华和叶淼林在文献[7]中给出了一个泛圈图的充分谱条件,同时在文献[8]中利用补图谱半径的界,讨论了泛圈图的谱条件。本文主要利用图及其补图的Wiener指数、hyper-Wiener指数,给出具有最小度条件的简单连通图是泛圈图的充分条件。

引理1(此结果已被《安庆师范大学学报(自然科学版》录用) 设G为n阶简单连通图,δ≥2,如果e( G )≥则G是一个泛圈图,除非G是一个二部图或G∈NPC。
下面给出本文的主要结论。
定理1设G为n阶简单连通图,δ≥2,如果

则G是一个泛圈图,除非G是一个二部图或G∈NPC。


若G是一个二部图或G∈NPC,则由引理1知,G不是泛圈图。
定理2设G为n阶简单连通图,Gˉ为n阶连通图,δ≥ 2,如果
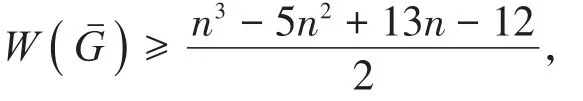
则G是一个泛圈图,除非G是一个二部图。
证明 假设G不是泛圈图,通过引理1,得
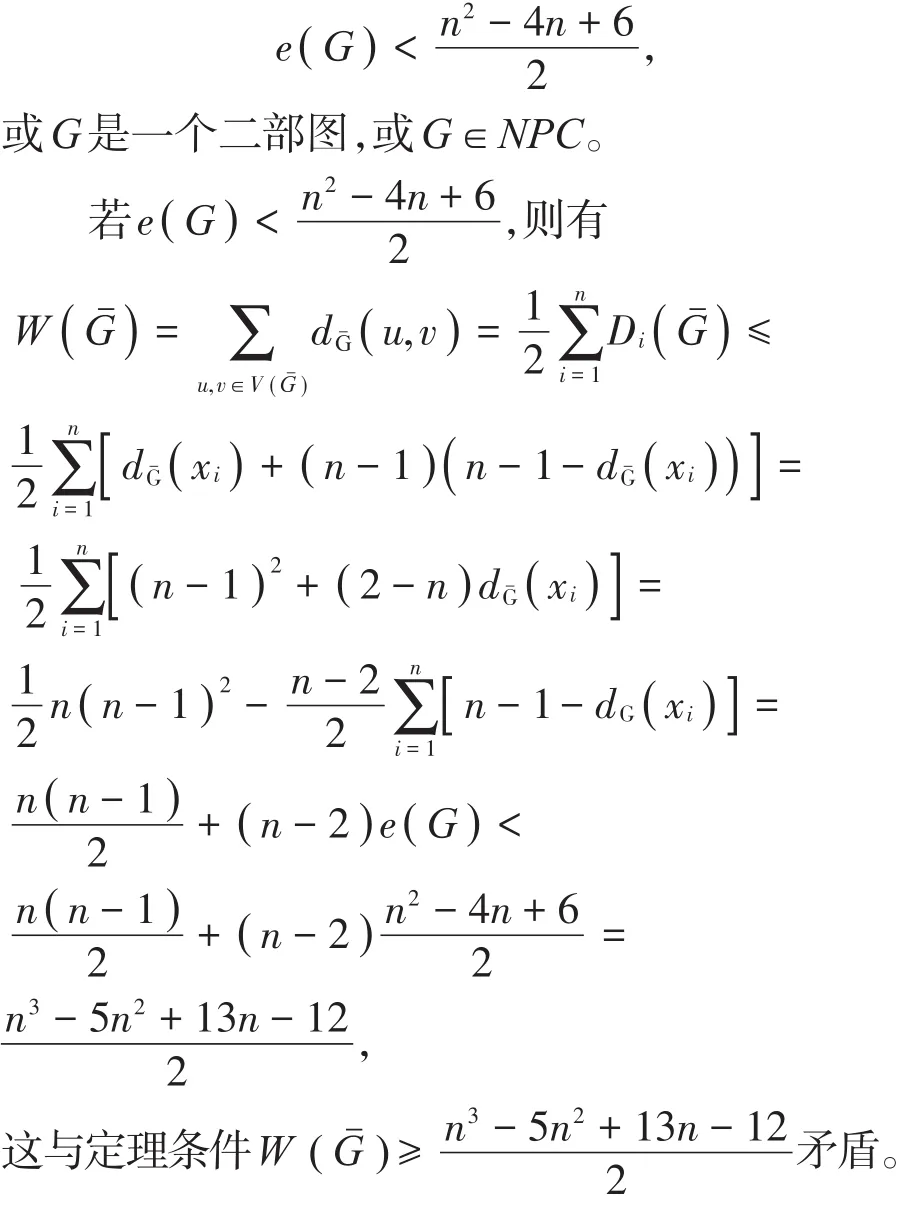
若G∈NPC,则其补图不是连通图,与已知条件矛盾。故假设不成立,即G是泛圈图。
若G是一个二部图,则由引理1知,G不是泛圈图。
定理3设G为n阶简单连通图,δ≥2,如果则G是一个泛圈图,除非G是一个二部图或G∈NPC。
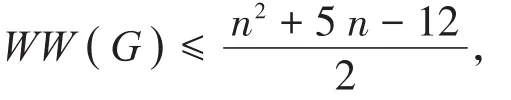
证明 假设G不是泛圈图,通过引理1,得或G是一个二部图或G∈NPC。
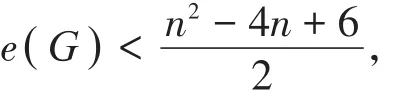

若G是一个二部图或G∈NPC,则由引理1知,G不是泛圈图。

证明 假设G不是泛圈图,通过引理1,得或G是一个二部图,或G∈NPC。

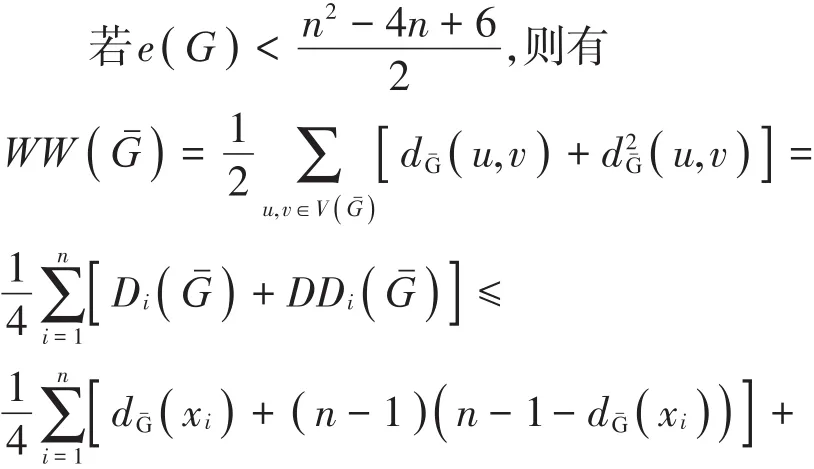

若G∈NPC,则其补图不是连通图,与已知条件矛盾。故假设不成立,即G是泛圈图。
若G是一个二部图,则由引理1知,G不是泛圈图。

