利用马尔科夫和灰色模型预测高校师资队伍

王韦霞

（安徽机电职业技术学院基础教学部，安徽芜湖241003）

高等教育创新发展要求不断调整优化师资队伍结构，而师资建设和规划需要各高校适时适当地制定计划和方案。但是，师资配置受到诸如办学规模、职称、师资评价及薪酬体系等社会经济各方面的制约，是一个复杂且不稳定的系统。如何合理优化师资队伍配置成为高校师资队伍建设的一个棘手问题。

本文以安徽省芜湖市某高校2014—2018年人员职称结构为案例，先根据马尔科夫链预测模型，利用多元回归理论建立多目标规划模型求解各类职称人员比例转移概率矩阵，预测出2019年各类职称人员比例；再借助灰色预测GM（1,1）模型对教师总数进行预测，从而预测出2019年该校各类职称人数。与传统的马尔科夫预测法相比，避免学校因减、增员造成的总人数变化而影响预测的准确性，该模型科学合理，反映了未来一定时期该校师资队伍发展规律，为高校师资队伍建设和规划提供参考。

1 基于回归分析的马尔科夫链模型预测

1.1 传统马尔科夫链模型原理[1]

假设存在一个马尔科夫链，其状态集合为{s1,s2,…,sm}，yt(j)（j=1,2,…,n）表示t时刻第j类职称人员的比例，初始矩阵:

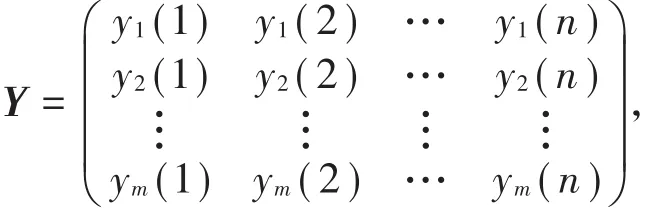
A=(pij)n×n为状态转移矩阵，由马尔科夫链的基本性质有：

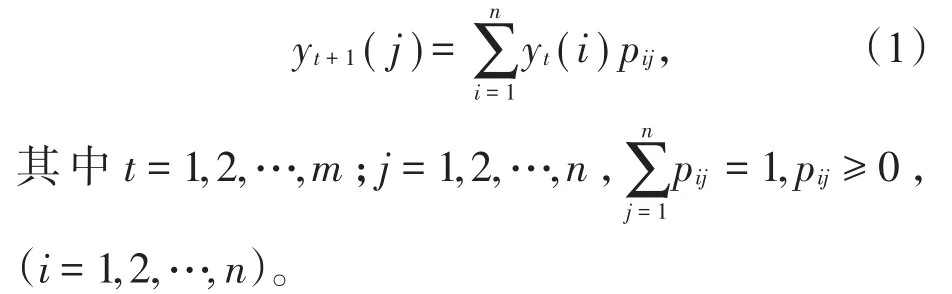
具体问题很复杂，马尔科夫状态转移矩阵无法直接由初始矩阵转化。传统马尔科夫状态矩阵的计算方法是通过某两个相邻时刻的转移概率来确定，但此方法要求各时刻的状态转移概率保持稳定，若随时间推移发生较大波动则预测效果不理想。为此，本文以芜湖某高校近5年职称人数发展规律为案例（见表1），利用多元回归分析及最优化理论去确定状态转移概率矩阵。

表1 某高校2014—2018年人员职称结构

1.2 基于回归分析的马尔科夫链模型原理[2-3]

假设在t时刻误差变量为εt(j),其中j=1,2,…,n。由（1）式有：

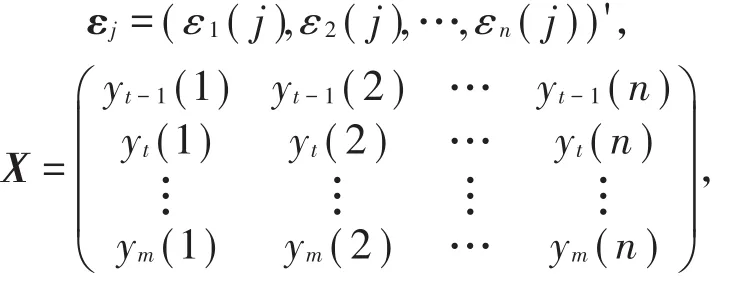
则（2）式可以写成

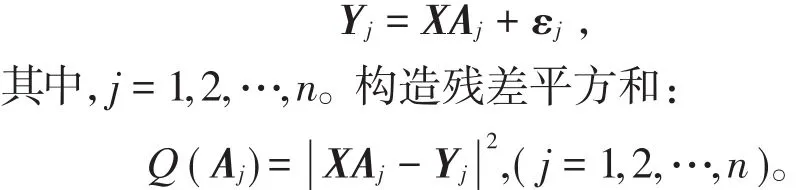
根据多元回归分析理论，满足Q(Aj)取得最小时，对应的Aj为状态矩阵A的第j列最优值。结合本文案例，因职称低级只能向本级或高一级转移的特点，则有p12=0,p13=0,p14=0,p23=0,p24=0,p31=0,p34=0,p41=0,p42=0。为此构造如下多元规划模型求解状态转移矩阵：

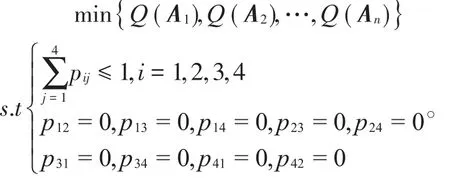
1.3 职称人员比例转移概率矩阵求解

根据1.2节的内容，再结合职称晋升由最低级逐步往高一级职称晋升、不存在跳级现象等特点，本文利用分层序列法，按Q(A4),Q(A3),…,Q(A1)的次序依次求出最优解。最优分层模型建立如下：

Step1:min Q(A4)

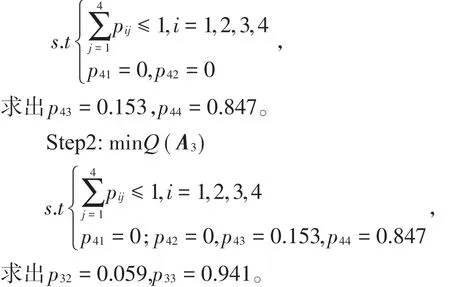
以此类推，依次求出满足Q(A2),Q(A1)最小时的A2,A1各元素，最后求解出状态转移矩阵：

根据职称人员比例转移概率矩阵，我们得出2015—2018年各类职称比例实际数据和预测数据，如表2所示。

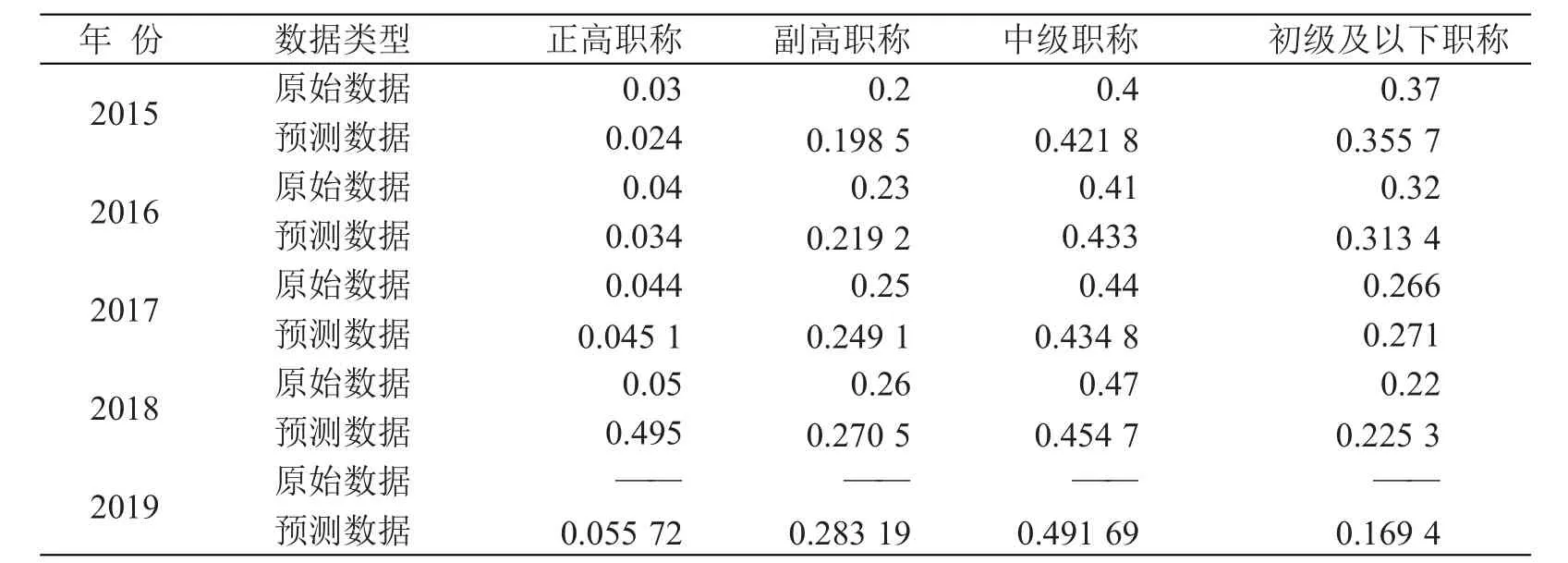
表2 2015—2018年各类职称比例实际数据和预测数据对比表

2 灰色GM（1,1）模型预测教师总人数

2.1 灰色GM（1,1）模型原理

灰色GM（1,1）模型是指一阶且仅有一个变量的微分方案预测模型，其基本思路如下：

(1)对原始数据序列的累加处理得到新的序列。设原始数据序列为x(0)=(x(0)(1),x(0)(2),…,x(0)(n))，对序列x(0)作一次累加生成，得到新的累加生成序列x(1)=(x(1)(1),x(1)(2),…,x(1)(n)),其中x(1)(k)=(i),k=1,2,…,n。

(2)通过最小二乘法估计a,u值，

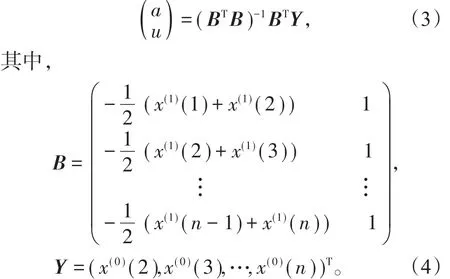
(3)建立一阶常微分方程模型

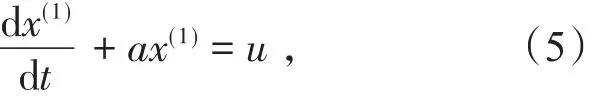
微分方程（5）就是灰色GM（1,1）预测模型，其中a,u为常数，（5）式满足初始条件x(1)=x(1)(t0)时的解为：

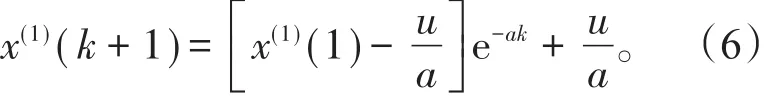
(4)预测值还原。由于（6）式得到的是一次累加生成数据序列的预测值，可通过累减生成原始数据序列的预测值，即：

2.2 教师总人数预测[4-8]

由2.1知教师总人数原始数据序列x(0)=[368,387,412,427,443]，对序列 x(0)作一次累加生成，得到新的累加生成序列为：

再由（3）式得到：[a,u]=[-0.0437,365.754 4]，由（5）式可知预测方程为：

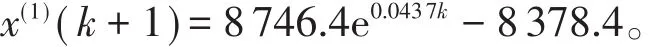
根据（7）式得出2015—2023年教师人数预测值分别为390、408、426、445、465、485、507、530、553，其中2015—2018年原始值与预测值对比情况见表3。

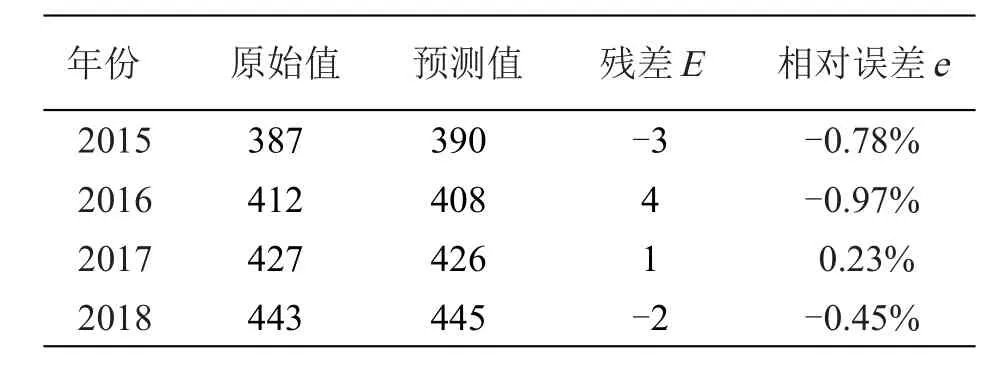
表3 2015—2018年原始值与预定值对比表

下面通过后验差对模型进行精度检验：

所有的 | E(i)-Eˉ|＜ 9.342 2，故小概率事件P{| E (i)-Eˉ|＜0.774S1}=1，根据预测等级对照表（见表4），因为P＞0.95,C=0.226＜0.35，可知预测合理。

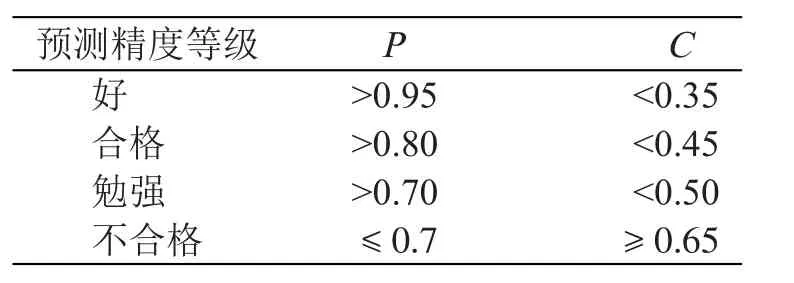
表4 预测等级对照表

3 预测结果检验

3.1 预测值与实际值误差分析

根据模型求解方案，本文对2015—2018年各类职称人数实际值和预测值进行对比，如表5所示。

由表5可见，预测值和实际值平均相对误差较小且误差逐年递减，即此模型能较合理反映近期情况。根据该预测方案，本文预测出2019年各类职称人数分别为正高职称25人，副高职称132人，中级职称229人，初级及以下职称79人。

3.2 与传统马尔科夫状态概率矩阵计算方法对比

通过对2016年、2017年职称人员比例数的转移数构造一步转移概率矩阵：

借助灰色预测得到2018年教师总数为445人，求出2018年各类职称人数实际值和预测值如表6所示。

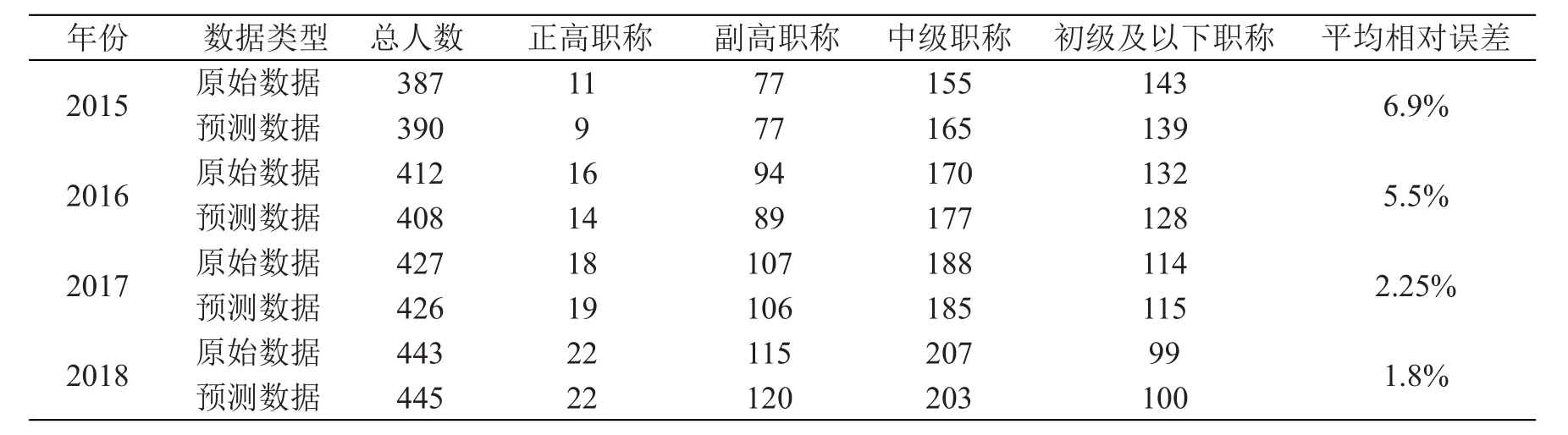
表5 2015—2018年各类职称人数实际值和预测值对比

表6 传统方法得到的2018年职称人数实际值和预测值对比

从平均相对误差值对比可知，改进的马尔科 夫状态概率矩阵计算方法预测效果更佳。（本文对比中传统计算方法以近两年的数据转移概率确定转移概率矩阵，若以最早的2014、2015年数据确定则平均相对误差更大），该方法得到的状态概率矩阵不仅具有一定时期代表性，而且消除了利用相邻两个时期状态概率转移作为一步转移概率矩阵陷入局部现象的弊端。

4 结 论

本文通过多元回归理论，构建了多目标规划模型求解高校职称人员比例状态转移矩阵，解决了状态转移矩阵难求且易陷入局部极值等问题，同时借助灰色预测GM（1,1）模型解决了马尔科夫状态转移仅局限于内部转移的缺点。通过两种预测方法结合运用，取长补短，很大程度上提高了预测精度。将该模型运用于高校职称人员预测，预测效果较好，在一定时期内反映了该校教师职称结构发展趋势，为高校师资队伍建设提供了科学的决策依据。