给定独立数的树的最大拉普拉斯谱半径

严亚伟，叶淼林，芦兴庭

（安庆师范大学数学与计算科学学院，安徽安庆246133）

设G是一个n阶简单无向图，记其顶点集为V={ v1,v2,…,vn}，边集 E={e1,e2,⋅⋅⋅,em}。NG(v)为G中与v相邻的点的集合，且记v的度数d(v ) = |NG(v ) |。G的任意子图H，任意的v∈V(G)，记 NH(v)=NG(v)⋂V(H)，dH(v)=|NH(v)|。若dG(v)=1，则称v是图G的叶子。Y(G)表示G中所有叶子的集合，称与叶子关联的边为悬挂边，与叶子关联的点为支撑点，用G-xy表示G删去边xy∈E(G)而得到的图，用G+xy表示图G增加边xy∉E(G)而获得的图。图G的独立数记为α(G)[1]，独立数是α的n阶树的集合记为Tn,α。图G的度矩阵记为D( G )=diag(d (v1),d(v2),⋅⋅⋅,d(vn)),其中d(vi)是顶点vi的度数，i=1,2,…,n。图G的邻接矩阵为A( G ) =(aij)n×n，如果 vivj∈E，则 aij=1；否则aij=0。图G的拉普拉斯矩阵为L(G)=D(G)-A( G )，L(G)的最大特征值称为图G的拉普拉斯谱半径，记为μ(G)。图G的无符号拉普拉斯矩阵为Q( G ) =D( G ) +A( G )，Q(G)的最大特征值称为图G的无符号拉普拉斯谱半径，记作q(G)。当G是连通的，L(G)是一个不可约矩阵，根据Perron-Frobenius定理，μ(G)对应的特征向量有一个正向量，称μ(G)对应的模为1的正特征向量为L(G)的perron向量。

图的谱半径的研究是谱图理论中的一个重要课题。文献[2]介绍了双圈图的谱半径，文献[3-6]介绍了给定条件的树的谱半径情况，其中文献[6]介绍了在所有给定阶数及给定独立数的树中具有最大谱半径的树，文献[7-8]介绍了特定条件下的图的最大谱半径以及最小谱半径。受文献[6]启发，本文给出Tn,α中拉普拉斯谱半径达最大的树，其中下面给出相关引理。

引理1设G是一个连通图，u,v是图G中的两个点，假设v1,v2,⋅⋅⋅,vs(1 ≤s≤d(v ) )是NG(v)NG(u)中的点，X=(x1,x2,⋅⋅⋅,xn)T是L( G )的Perron向量，其中xi与点vi( 1 ≤i≤n )对应，图G*是图G删去边vvi( 1 ≤i≤s )，增加边uvi得到的图。如果xu≥ xv，那么μ( G ) ＜ μ(G*)。

证明 由文献[4]可知，引理1对于无符号拉普拉斯谱半径q( G )是成立的。同时对于偶图G，L( G )和Q(G )具有完全相同的特征值。因为树是偶图，故引理1得证。

引理2[6]设T是一棵树，Y( T )为树T中所有叶子的结合，S( T )为树T的最大独立集，那么，对于每一个树T都存在一个最大独立集S(T )，使得Y( T ) ⊆S( T )。

现构造3种图，具体如图1所示。

(1)在星图K1,e-1中每个点上粘上至少一条悬挂边得到的图，记为n-e；

(2)在星图K1,e中每个度为1的点上粘上至少一条悬挂边得到的图，记为S2n,n-e；

(3)在星图K1,e-1中每个度为1的点上粘上一条悬挂边，度为e-1的点上粘上n-2e+1条悬挂边得到的图，记为S*n,n-e。

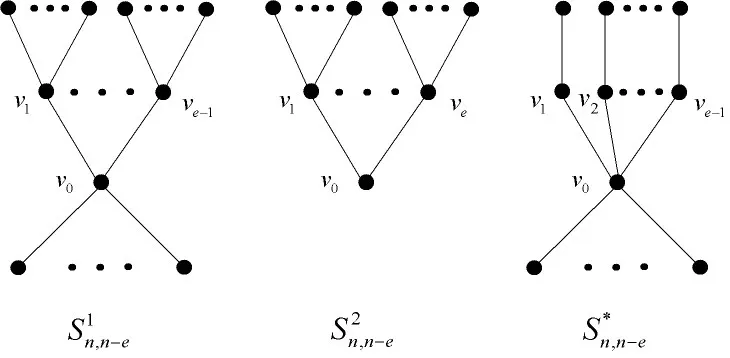
图1

下面给出本文的主要结果。

定 理1 若T∈Tn,n-e( e ≥2 ) ，则 μ( T ) ≤μ(n-e)，当且仅当T=,n-e时等号成立。

证明 选取树T∈Tn,n-e( e ≥2)使其拉普拉斯谱半径尽可能的大。 设X=(x1,x2,⋅⋅⋅,xn)T为L( G )的Perron向量，这里xi与点vi( 1 ≤i≤n )对应，可以得到相关结论。

（i）当s＞0且t＞0时，如图2所示。

根据引理2，树T中存在一个最大的独立集S( T )，使得Y( T ) ⊆S( T )，当s＞ 0且t＞ 0时，有

因为在上述两种变形中

（ii）当s=0且t＞0或者s＞0且t=0时，如图3所示。

不失一般性，令s=0且t＞0，由引理2，树T中存在一个最大的独立集S(T ) ，使得Y( T ) ⊆S( T )，且

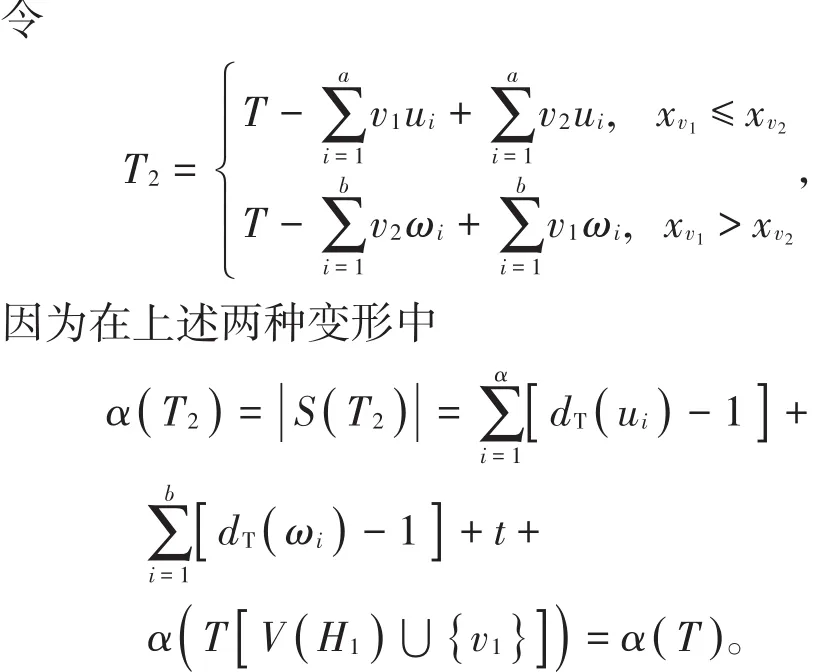
因 此 T2∈Tn,n-e，同 理 由 引 理 1，可 得μ( T ) ≤ μ( T2)，矛盾。

（iii）当s=0且t=0时，如图4所示。

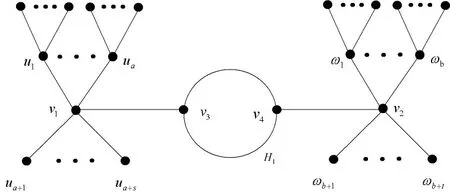
图2

根据引理2，树T中存在一个最大的独立集S( T )，使得Y(T ) ⊆S( T )，且有

因为在上述两种变形中

因为在上述两种变形中