动静转化 巧解高考压轴题
——几道高考题引发的换位思考
2018-12-27 08:30:06罗先文
数理化解题研究 2018年34期
罗先文
(湖南省常德芷兰实验学校 415000)
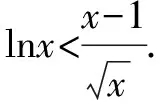
问题1 (2014天津理科22)设f(x)=x-aex(a∈R).已知函数y=f(x)有两个零点x1,x2,且x1 (1)求a的取值范围; 这一小问的解答,充分利用了数形结合的思想,过程简单流畅,易于理解. (2)依题意有,x1-aex1=0 (1);x2-aex2=0(2). 又对(1)式两边取对数得:lnx1=lna+x1(3);lnx2=lna+x2(4). 第二小问的解答,采用了动静转换的思想,把参数a,由静变为动,通过讨论字母x1,x2关于a的单调性,使问题迎刃而解. 问题2 (2016年全国卷2,第21题) 解 (1)略. 问题3 (2010年安徽卷理科,第21题)已知函数f(x)=ex-2x+2a. (1)求f(x)的单调区间和极值; (2)求证:当a>ln2-1且x>0时,ex>x2-2ax+1. 解 (1)略. (2)以a为主变元,x视为常数.设:g(a)=2xa+ex-x2-1,是关于a的增函数,g(a)≥g(ln2-1)=2x(ln2-1)+ex-x2-1.记p(x)=2x(ln2-1)+ex-x2-1,那么p′(x)=ex-2x+2ln2-2(x>0). 容易证明:p′(x)≥0(x>0),所以p(x)是关于x的增函数,故p(x)>p(0)=0,从而g(a)>0,也即,ex>x2-2ax+1成立.证毕. 由此可见,合理的应用数学思想方法解决数学问题,尤其是难题,能够减少尝试或失败的次数,能够节省探索的时间和解题的长度,体现出选择的机智和组合的艺术.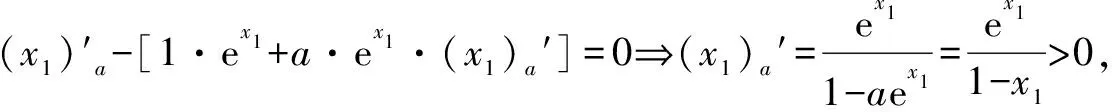
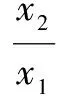
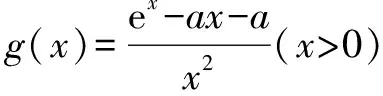

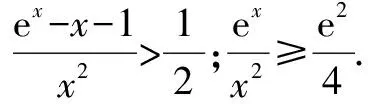
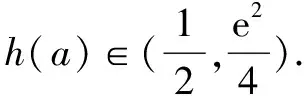
猜你喜欢
中学生数理化(高中版.高二数学)(2021年9期)2021-11-05 08:40:50
齐齐哈尔大学学报(自然科学版)(2021年2期)2021-03-19 05:18:00
小资CHIC!ELEGANCE(2021年45期)2021-01-11 03:51:12
中学生数理化·高一版(2020年11期)2020-12-14 07:35:20
中学生数理化·八年级物理人教版(2019年9期)2019-11-25 07:33:00
新世纪智能(高一语文)(2019年4期)2019-06-25 10:06:36
中学数学杂志(高中版)(2019年2期)2019-04-08 01:34:20
新世纪智能(数学备考)(2018年9期)2018-11-08 11:07:38
北京航空航天大学学报(2017年1期)2017-11-24 05:22:16
数理化解题研究(2016年34期)2017-01-09 10:51:22

