例说“一题多解”——一道三角形问题的教学思考

汤晓玲

(江苏省海门中学 226100)

一道好的数学试题，它应该可以从多个角度去解决，可以给学生更大的发挥空间，从不同的角度、不同的维度去思考、解决问题，使学生真正做到将数学知识融会贯通，灵活应用.笔者在近期的高三复习中就碰到了诸多好题，下面举一道解三角形问题，从多角度分析，可以给出不同的解法，充分应用一题多解，培养学生的思维.

例题 若点G为△ABC的重心，且AG⊥BG，则sinC的最大值为____.

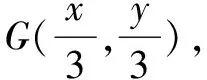
答案是正确的，其实解题过程不够完善，究其根本，为什么点C在y轴上时角C最大呢？事实上，我们可以从一般情况来解.

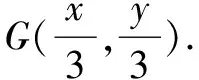
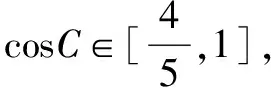
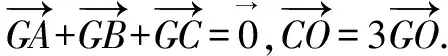
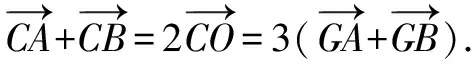
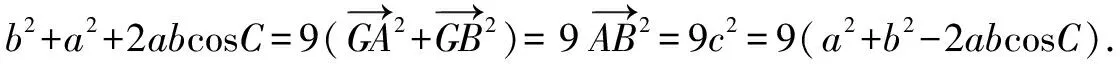
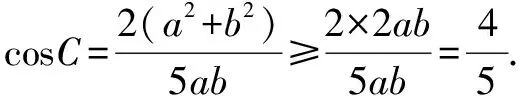
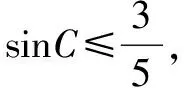
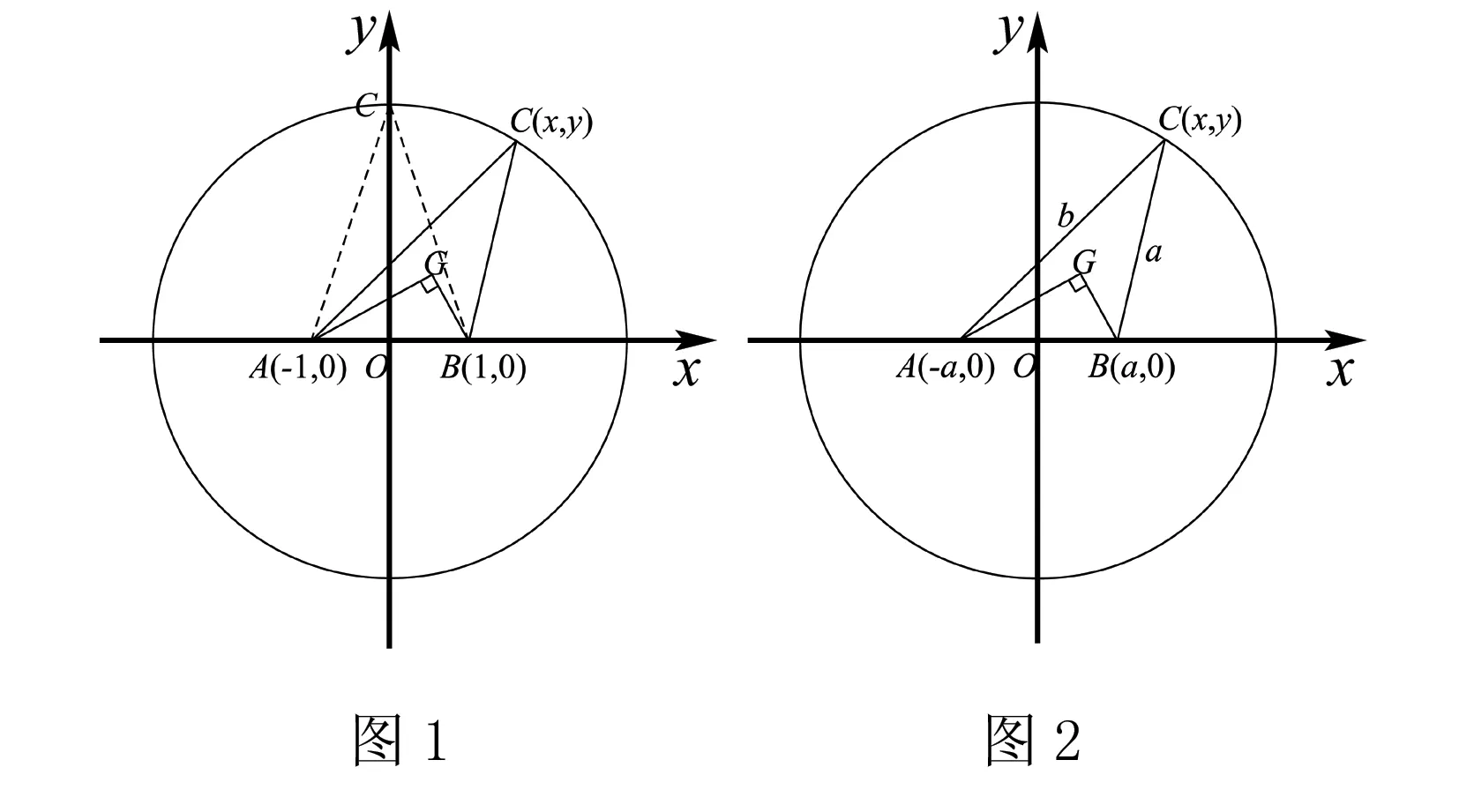
解法3要比解法2更巧妙、简洁一些.同样建系来解决，一般我们都选择特殊位置，使尽可能多的点在坐标轴或与坐标轴平行的直线上，关注到已知条件中“AG⊥BG”，是否可以考虑将G点作为原点？可以尝试一下.

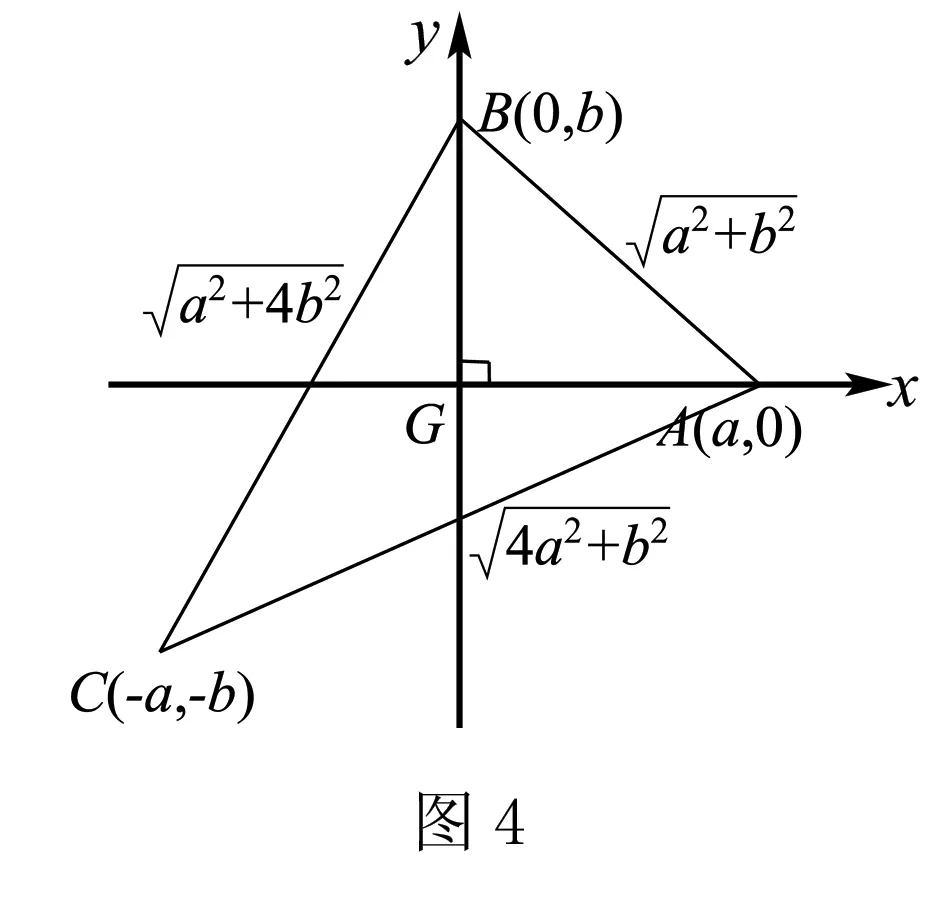
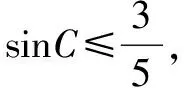
比较以上几种解法，发现解法3和4相对稍微简洁一些，从“G为重心”这个条件出发，利用它的向量特征可以直接得到边角关系，结合基本不等式找到最值；如果抓住“AG⊥BG”这个条件的话，可以以G为原点来建系，再考虑G为重心，可以得到点C(-a，-b)，这样可以得到三条边长，利用余弦定理，列出cosC的表达式，结合基本不等式求出最值.

一道数学题的一题多解，因思考的角度不同可得到多种不同思路.在我们的教学过程中，广阔寻求多种解法，有助于拓展学生的解题思路，发展学生的思维能力，提高学生分析问题的能力.在例题讲解时运用一题多解，不仅可以得到它的多种解法，关键是可以从中获得解题规律、技巧，从而举一反三.

因此我们在具体解题时，要学会从多角度观察、分析、使用题设条件，综合使用多种方法，提高思维质量，打开解题思路，逐步加强解题能力，才能找到较简洁的解法从而适用各种考试.

“一题多解”的好处就是培养发散思维，提升解题能力，寻找各类题型的解题捷径.通过“一题多解”，我们能在一个问题里复习到多个知识点，然后在多个知识点之间牵线搭桥，进而养成良好的思维能力，使得数学的学习变成一个探索、发现、提高的过程，不断地提高自己的思维品质，从而真正达到提升自己的能力和档次.