关注数列“姊妹题” 体验精彩“无极限”
薛映红
(河南省郑州市《中学生学习报》社有限公司 450000)
本文给出以下几组关于数列“姊妹题”的具体解析过程,以切实帮助读者提高分析、解决数列问题的实际能力,进一步拓宽思维视野.
【第一组“姊妹题”】
例1 (1)已知知数列{an}对任意的p,q∈N*满足ap+q=ap+aq,且a2=-6,那么a10等于( ).
A.-165 B.-33 C.-30 D.-21
(2)已知数列{an}对任意的p,q∈N*满足ap+q=ap·aq,且a3=-8,那么a10等于( ).
A.256 B.1024 C.-256 D.-1024
解析 (1)取p=n∈N*,q=1,则有an+1=an+a1⟹an+1-an=a1,∴数列{an}是等差数列,其首项是a1,公差也是a1.又取p=q=1得a2=a1+a1,而a2=-6,∴a1=-3.从而a10=a1+9a1=10a1=-30,故选C.
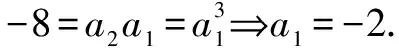
评注 这两问求解的关键都在于通过灵活地赋值,认清数列{an}的特性,并加以充分运用.
【第二组“姊妹题”】
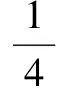
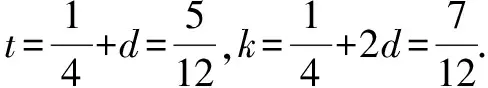
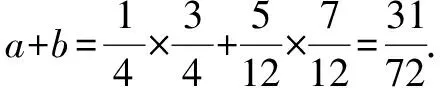
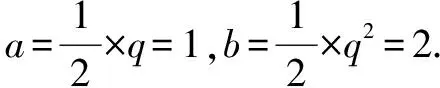
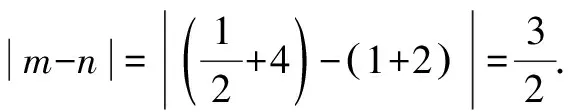
评注 第(1)问求解的关键在于,综合考虑根与系数的关系及等差数列的特性(当正整数n+m=p+q时,对于等差数列{an}有an+am=ap+aq),巧设对应的两个二次方程的根;第(2)问求解的关键在于,综合考虑根与系数的关系及等比数列的特性(当正整数n+m=p+q时,对于等比数列{an}有an·am=ap·aq),巧设对应的两个二次方程的根.
【第三组“姊妹题”】
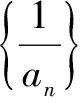
A.3nB.n2+2nC.3n2D.3n
(2)在等比数列{an}中,a1=2,前n项和为Sn.若数列{an+1}也是等比数列,则Sn等于( ).
A.2n+1-2 B.3n-1 C.2nD.3n-1
解析 (1)∵{an}是等差数列,∴an+1+an-1=2an(n≥2).
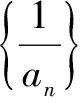
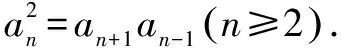
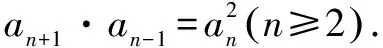
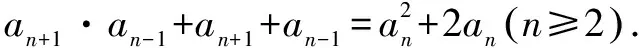
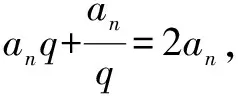
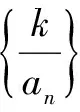
【第四组“姊妹题”】
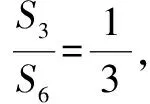
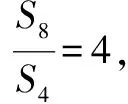
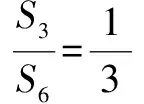
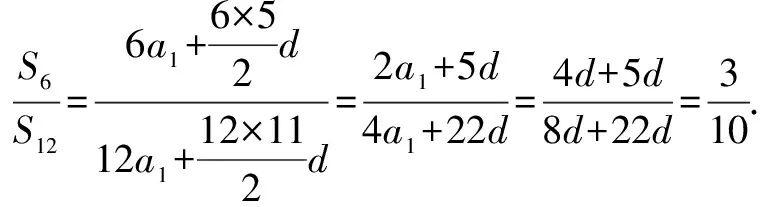
故选A.
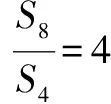
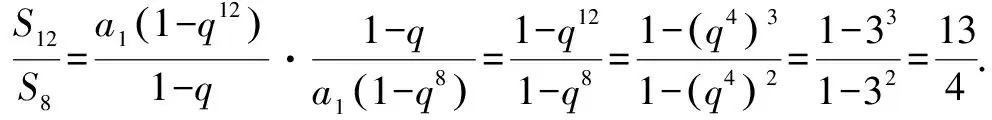
解析二 (简捷解法)(1)由于目标是求比值,于是可设S3=1,则S6=3.∵易知S3,S6-S3,S9-S6,S12-S9构成等差数列,∴1,2,S9-3,S12-S9构成等差数列.
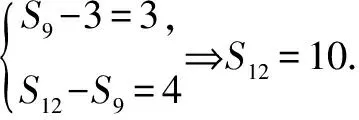
(2)由于目标是求比值,于是可设S4=1,则S8=4.∵S4≠0,∴易知S4,S8-S4,S12-S8构成等比数列,∴1,3,S12-S8构成等比数列.
评注 (1)设等差数列{an}(公差为d)的前n项和为Sn,则连续k项和,即Sk,S2k-Sk,S3k-S2k,…也构成等差数列(公差为k2d);(2)设等比数列{an}(公比为q)的前n项和为Sn,若Sk≠0,则连续k项和,即Sk,S2k-Sk,S3k-S2k,…也构成等比数列(公比为qk).
【第五组“姊妹题”】
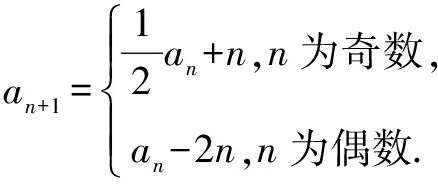
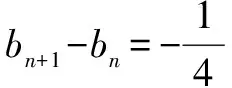
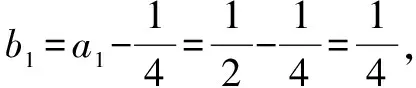
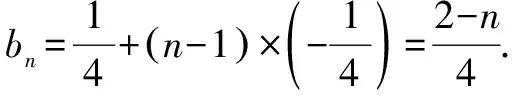
【第六组“姊妹题”】
例6 已知在数列{an}中,相邻两项an,an+1是方程x2+3nx+bn=0的两个根,若a10=-17,求b51.
∵由(1)得an+1+an+2=-3(n+1), (3)
∴由(3)-(1)得an+2-an=-3,∴易知数列a1,a3,a5,…,a2n-1和a2,a4,a6,…,a2n都是以-3为公差的等差数列.
又由(1)及a10=-17得a11=-30-a10=-13.
于是,a51=a11+(26-6)×(-3)=-13-60=-73,a52=a10+(26-5)×(-3)=-17-63=-80.故由(2)得所求b51=a51·a52=-73×(-80)=5840.
评注 这种解法的切入点是以“作差”的方式活用递推式.在等差数列a1,a3,a5,…,a2n-1中,a51是第26项,a11是第6项;在等差数列a2,a4,a6,…,a2n中,a52是第26项,a10是第5项.
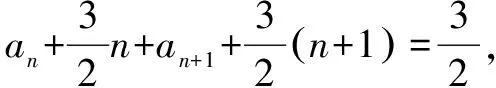
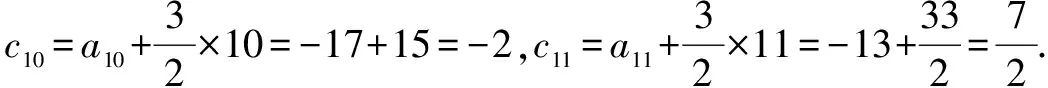
评注 这种解法的切入点是通过适当变形,产生一个新数列的相邻两项之和为常数.一般地,若an+an+1=t(t为常数),则数列{an}是以2为周期的周期数列,即所有奇数项相同,所有偶数项也相同.
例7 已知在数列{an}中,相邻两项an,an+1是方程x2+bnx+3n=0的两个根,若a3=27,求b10.
∵由(2)得an+1·an+2=3n+1, (3)∴由(3)÷(2)得∴易知数列a2,a4,a6,…,a2n和a1,a3,a5,…,a2n-1都是以3为公比的等比数列.
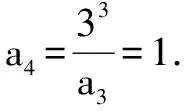
于是,a10=a4·35-2=1×27=27,a11=a3·36-2=27×81=2187.故由(1)得所求b10=-(a10+a11)=-(27+2187)=-2214.
评注 这种解法的切入点是以“作商”的方式活用递推式.在等比数列a2,a4,a6,…,a2n中,a10是第5项,a4是第2项;在等比数列a1,a3,a5,…,a2n-1中,a11是第6项,a3是第2项.
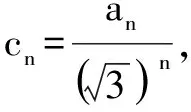
于是,数列{cn}是以2为周期的周期数列.
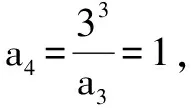
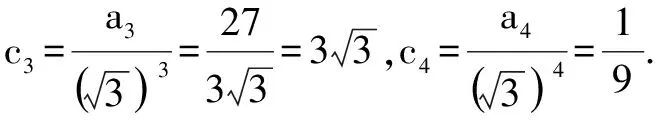
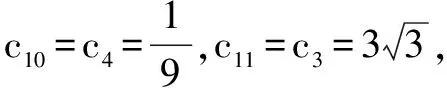
故由(1)得所求b10=-(a10+a11)=-(27+2187)=-2214.
评注 这种解法的切入点是通过适当变形,产生一个新数列的相邻两项之积为非零常数.一般地,若an·an+1=t(t为非零常数),则数列{an}是以2为周期的周期数列,即所有奇数项相同,所有偶数项也相同.
综上,只要我们善于运用“类比思想”去做进一步的归纳、探究,那么我相信关注数列“姊妹题”, 一定会体验到其中的精彩“无极限”!

