一类不等式与抽象函数相结合问题的探究与教学思考
内蒙古自治区呼和浩特市内蒙古师范大学附属中学 (邮编:010020)
在高三复习过程中,有一类不等式与抽象函数相结合的问题经常出现在高考卷或各地模拟卷中,这类问题是考试中的热点问题,也是学生不易掌握的知识点,究其原因,很多学生并不知道解决此类问题的着眼点在哪,往往容易被一些无关信息所迷惑,也无法察觉陌生问题与熟悉问题之间的联系. 针对这种情况,笔者在教学过程中设计了一个微专题,让学生体会复杂问题与基本问题之间的本质性联系,拨开冗杂的条件,更好的理解这类问题的本质,收到了较好的教学效果. 现整理成文,与读者探讨.
1 问题的提出
例1 已知函数f(x)在区间(-∞,+∞)上单调递增,且f(2a-1)>f(1-a),则实数a的取值范围是__________.
解析这类问题的特点是函数f(x)解析式未知,属于抽象函数,若要解不等式,最关键的步骤是探索函数的单调性,借助单调性可以“脱掉”函数的对应关系f,题目也就迎刃而解了.
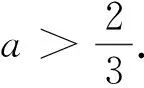
注例1是学生非常熟悉的题目,以这个问题为开端的目的是要通过简单的题目强调解决问题的基本方法,这样学生的注意力就会集中在方法本身而不是繁杂的条件,能更好的理解方法的本质,以这个简单的问题为“生长点”,继续进行下面的探索.
例2 已知函数f(x)在区间(-1,1)上单调递增,且f(2a-1)>f(1-a),则实数a的取值范围是__________.
解析在分析问题时要先识别问题,然后再选择合适的处理方法,这个题目与例1类似,仍然属于不等式与抽象函数相结合的问题,但是本题中函数的定义域为(-1,1),除了考察函数的单调性这一关键信息外,还应注意这一易错点.
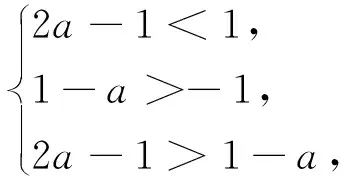
通过上述两个例题,引导学生识别此类问题的特征及解决问题的方法:这类问题一般以抽象函数为背景,建立相应的不等式问题,解决问题的关键是探索抽象函数的单调性,在建立同解的不等式或不等式组时,要特别注意函数的定义域.
2 基本问题的改编与拓展
2.1 隐藏函数的单调性信息
例3 已知函数f(x)是定义在(-∞,+∞)上的奇函数,且在区间[0,+∞)上单调递增,若f(2a-1)>f(1-a),则实数a的取值范围是__________.
解析根据条件易知本题仍然属于不等式与抽象函数相结合问题,但是题中仅仅给出函数的一段单调区间,借助函数的对称性(本题特指函数的奇偶性),容易得到函数完整的单调区间.
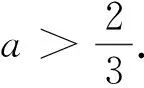
注随着问题难度的增大,解决问题的关键信息会越来越隐蔽,但是当识别清楚问题之后,我们知道题中所给条件的唯一目的就是想要告知抽象函数的单调性,这就可以直接面对难点:通过性质探索单调性,避免了在复杂条件下的不知所措.
例4 已知函数f(x)在R上满足f(2-x)=-f(x),且在区间[1,+∞)上单调递增,若f(2a-1)>f(1-a),则实数a的取值范围是__________.
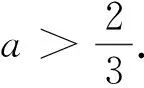
注本例可以看作例3的推广,借助函数图象的对称性,可以得到函数在定义域内的单调区间,使得问题获解.
例5 已知函数f(x)是定义在(-∞,+∞)上的偶函数,且在区间[0,+∞)上单调递增,若f(2a-1)>f(1-a),则实数a的取值范围是__________.
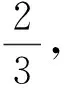
例6 已知函数f(x)在R上满足f(2-x)=f(x),且在区间[1,+∞)上单调递增,若f(2a-1)>f(1-a),则实数a的取值范围是__________.
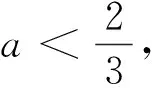
注类比例3和例4,上述例5和例6也是利用函数图象的对称性探寻抽象函数的单调性,且例6也可以看作例5的推广,所不同的是,函数图象关于轴对称,借助单调性转化为2a-1和1-a与轴距离的远近问题,回避分类讨论.
例7 已知函数f(x)=x3+sinx,x∈(-1,1),且f(2a-1)>f(1-a),则实数a的取值范围是__________.
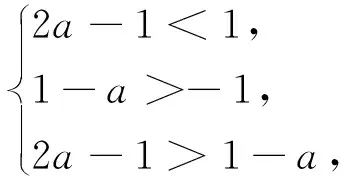
注本例中虽然知道了函数f(x)的解析式,但并不是通过直接代入解析式来解不等式,由于这样的不等式无法直接解出(给出解析式也不能直接带入获解,这就等同于没给),因此,条件中提供解析式的目的是为了探寻函数的单调性,这样命制的题目隐蔽性强,需要学生深刻理解问题的特征才能进行合理的转化,因此,把这类题目也归为不等式与抽象函数相结合的问题. 类似地,在教学的过程中也给出了下面两个例子,以便更好地理解问题的本质特征.
例8 已知函数
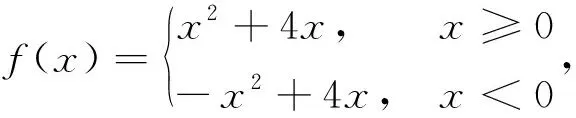
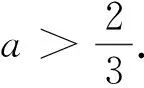

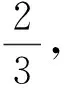
2.2 隐藏所研究函数的信息
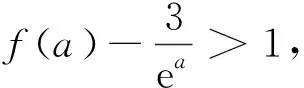
注本例与前面例题的显著区别是所研究的函数并非已知的抽象函数f(x),需要结合所求来寻找便于解决问题的新函数,然后借助新函数的单调性将所考察的不等式转化为等价的不等式或不等式组. 目前,这种命制问题的方式更广泛的被应用在高考或模拟考的试卷中,隐蔽性更强,学生不容易识别,在寻找新函数的过程中,可以借助条件中与导数相关的不等式(这个条件是帮助寻找新函数的单调性的)和所求的不等式(这个条件可以转化为与新函数相关的不等式)这两个关键信息,对学生的能力要求较高,在课堂教学过程中,笔者又借助下面两个例题帮助学生体会如何寻找所考察的新函数.
例11 已知定义在R上的函数f(x)的导函数为f′(x),满足f(-x)+f(x)=x2,且在区间(0,+∞)上有f′(x) 例12 已知定义在R上的函数f(x)的导函数为f′(x),满足f′(x)>2018f(x),且f(0)=1,若f(lna) 注复合函数研究起来比较困难,而且思维量较大,这里采用换元法,问题便迎刃而解了,合理利用重要的数学思想方法对于问题的转化会起到积极的促进作用. 在高中数学的教学过程中,经常要根据数学模块中的核心知识点、重要的方法和技巧,亦或学生的易错点等制定一些教学专题. 专题,顾名思义就是要有针对性的解决某一个问题,在制定专题的过程中,设计的起点应该是学生容易理解的常规问题,通过这个常规问题让学生体会核心知识点、重要的方法或技巧,接下来通过设计的一系列变式或题组(即增加迷惑性条件或易错点)进一步让学生感受问题的本质,教学过程中要在问题的转化上下功夫,重点强调这些变式或题组与最初的基本问题之间的联系与区别. 所谓联系,就是引导学生发现这些题目与基本问题的本质相同;所谓区别,就是让学生彻底弄清繁杂信息的作用,与基本问题的差别,不要因曲解条件而产生对问题本质的错误理解. 专题教学的目的也是让学生从“学会”向“会学”转变,在提高学生数学素养的同时,让他们感受思维的力量,感悟数学之美.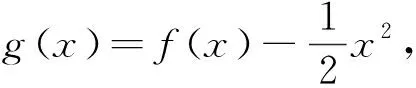
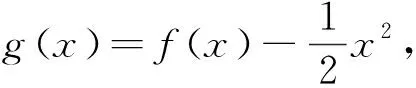

3 复习过程中专题的制定与教学思考

