一种基于UPF的轴承剩余寿命预测方法
文 娟, 高宏力
(西南交通大学 机械工程学院 先进驱动节能技术教育部工程研究中心,成都 610031)
作为一种关键零部件,轴承被广泛应用于各种机械系统中。通常轴承的工况复杂,工作环境恶劣,因而频繁出现各种故障。一旦轴承出现故障,可能会造成整个机械系统停机,带来灾难。因此,适时监测轴承状态,并根据状态监测结果指导维修计划对于提高系统可靠性与降低生产成本具有重要意义。状态维修(Condition-Based Maintenance)主要包括两个部分,故障诊断和故障预警[1-3]。故障诊断的主要任务为判断系统能否正常工作,一旦不能工作,将会停机并更换故障零部件。故障预警的主要任务为判断系统的当前状态,并根据当前状态对系统的剩余服役寿命进行预测,并使用预测结果指导维修计划的制定。准确的故障预警能够在确保安全的情况下节约维修费用,因而受到了越来越多研究者的关注。
通常寿命预测可以分为两种,基于数据驱动的方法和基于模型的方法。数据驱动的方法试图通过机器学习方法建立状态监测数据与系统退化过程之间的关系。Tian等[4]提出了一种利用失效数据和未失效悬疑数据建立人工神经网络(Articial Neural Network)寿命预测模型的方法。Tran等[5]利用时间序列技术和支持向量机(Support Vector Machines)对剩余寿命进行预测。与数据驱动方法不同,基于模型的方法主要通过建立能够反应退化过程的数学模型来对剩余寿命进行预测。Gebraeel等[6-8]在数学模型的建立方面完成了许多工作。模型建立后,通常需要利用贝叶斯推断理论结合状态监测数据估计系统状态和模型参数,并完成寿命预测。
传统的实现贝叶斯推断的方法有卡尔曼滤波(Kalman filter, KF)和扩展卡尔曼滤波(Extended Kalman filter, EKF),都已成功应用到寿命预测中[9]。粒子滤波(Particle filter, PF)是一种利用一群具有特定权值的粒子近似状态估计值的方法。与KF方法不同,PF算法不受限于高斯假设,特别适用于非线性非高斯应用场景,已经在寿命预测领域得到了许多应用[10-11]。但是,PF算法存在粒子退化的缺陷,在经历了一定的迭代步数后,许多粒子的权值变得极小。而粒子的退化会影响剩余寿命预测的准确度[12],因此,如何有效降低PF方法中的粒子退化程度,进而减小预测误差,是基于PF的寿命预测方法中存在的一大问题。选择合适的重要性采样概率分布函数是解决这一问题的有效方法。无迹粒子滤波(Unscented Particle filter, UPF)就是一种利用这种方式解决粒子退化问题的改进粒子滤波算法[13]。UPF结合了PF和无迹卡尔曼滤波(Unscented Kalman filter, UKF)的优点,利用UKF算法获得一个合适的重要性采样概率分布,从而有效降低粒子退化程度。为了解决基于PF轴承剩余寿命预测中的粒子退化问题,本文提出一种基于UPF的轴承剩余寿命预测方法,即通过UPF结合数学模型与轴承的状态监测信号估计轴承的当前健康状态,并给出其剩余寿命的估计值。
1 UPF算法
1.1 贝叶斯估计
大部分的动态系统都可以由两个方程描述,状态转移方程和观测方程为
θt=ft(θt-1,nt-1)
(1)
yt=ht(θt,vt)
(2)
式中:ft—Rnθ×Rnn→Rnθ为上一时刻到当前时刻的状态转移函数;ht—Rnθ×Rnv→Rny为当前状态θt的观测函数;nt为独立同分布过程噪声;vt为独立同分布测量噪声。
分别使用θ0:t={θ0,…,θt}和y1:t={y1,…,yt}代替当前所有状态和所有观测值。我们的目的是得到后验概率p(θ1:t|y1:t)。根据马尔科夫过程特性,我们无需追踪所有已有状态,只需递归地计算p(θt|y1:t)便可得到后验概率。具体地,每一时刻的先验概率密度分布函数和后验概率密度分布函数分别如式(3)和式(4)所示
(3)
(4)
1.2 UPF算法
PF算法的本质是利用一群具有特定权值的粒子来近似系统状态,通过更新粒子权值和粒子来实现最优估计。具体地,系统状态后验概率密度分布函数可以表示为
(5)
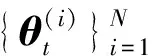
标准PF算法中,通常采用系统的先验分布作为重要性采样分布,这种做法能够简化计算过程,但是容易使PF算法陷入粒子退化问题中。与标准PF算法不同,UPF利用UKF生成重要性采样分布,充分利用最新的观测值,能够有效地解决粒子退化问题。
UPF的具体实现步骤如下:


步骤3根据式(6)利用当前时刻t的测量值更新各粒子所对应的权值。
(6)
并根据式(7)对权值进行归一化处理。
(7)
步骤4重采样。为了增加有效粒子的数量,提高计算效率,需要移除权值极小的粒子,并复制权值较大的粒子,这个过程称之为重采样。一个简单的实现过程如下[14]:


(8)
步骤5状态估计。利用更新后的粒子及其权值估计当前时刻t的状态
(9)
步骤6然后返回至步骤2,重复之后的步骤,直到t=T(T为测量值的数量)。
2 基于UPF的轴承剩余寿命预测方法
轴承的整个工作周期可以分为三个阶段,正常阶段,退化阶段以及失效阶段。当轴承处于失效阶段时,意味着轴承已经不能正常工作,需要进行更换。因此,本文只考虑前两个阶段的剩余寿命预测。轴承的状态监测数据有振动信号、温度和声发射等。其中,由于振动信号采集方便,而且对轴承的性能退化十分敏感,因而被广泛应用于轴承的故障诊断和剩余寿命预测中[15]。因此,本文从振动信号中提取特征,将其作为轴承性能退化的指标。
本文提出的方法如图1所示。根据已知的历史失效轴承数据利用随机过程模型建立轴承的退化模型。在针对具体轴承进行寿命预测时,首先判断其是否开始退化,当检测到其开始退化时,利用UPF方法结合数学模型和测量数据,更新模型参数,估计轴承的退化状态,并实现轴承的剩余寿命预测。通常,信号的不同特征描述的是信号的不同方面,因而能从不同角度反映轴承的退化状态。在轴承的故障诊断与寿命预测中,峭度对于早期故障比较敏感,但对于故障的发展恶化并不敏感,而均方根值(Root Mean Square, RMS)反映的是振动能量随故障发展的增长,因而对于轴承故障发展程度较为敏感。因此,本文利用峭度监测故障的出现,采用RMS评估轴承的故障发展程度,并预测其剩余寿命。

图1 基于UPF的轴承寿命预测方法流程图Fig.1 Flowchart of the proposed method
2.1 轴承退化检测
在轴承的整个工作周期中,轴承有很长一段时间都处于正常工作状态。在这个阶段,我们没有必要预测轴承的剩余寿命。因此,检测轴承的退化起点,仅在轴承的性能退化阶段预测其剩余寿命能够有效节约计算资源。此外,正确区分正常状态与退化状态的监测数据,能够有效避免正常状态数据的干扰,提高寿命预测的准确度。因此,本文在针对具体轴承进行寿命预测时,先判断其工作状态,当检测到其开始退化时,才开始预测其剩余寿命。
轴承振动信号的峭度是一个无量纲参数,与轴承的负载及参数无关。通常,峭度指数对于轴承的早期故障比较敏感,但对于故障的发展与状态恶化并不敏感。因此,本文采用振动信号的峭度值来判断故障的出现,即确定轴承剩余寿命预测的起始点。首先,计算轴承正常工作状态下振动信号峭度值的均值μ与标准差σm,定义轴承状态正常的峭度值区间为[μ-3σm,μ+3σm]。状态监测过程中,当tf时刻的峭度值mf超出该区间时,则认为轴承振动信号出现异常。由于振动信号的采集以及特征提取中存在一定的随机误差,会造成误判。为了消除这一影响,引入Li等研究中的触发机制来判定轴承的退化起始点,具体步骤如下:
步骤1首先,定义l= 0,当峭度值第一次超出3σm时,定义该时刻点为FPT0;
步骤2令l=l+1,当时间点tf满足连续l+1个时间点的峭度值{mf+k}k=0:l满足{|mf+k-μ|>3σm}k=0:l,则定义时刻tf为FPTl;
步骤3使l由1逐渐增大直到l满足FPTl=FPTl-1,则认为轴承此时出现故障,并定义FPTl为轴承的剩余寿命预测起始点。
通常,由随机噪声造成的异常状态不可能连续出现l+1次,因此上述触发机制能够很好地消除随机噪声对轴承退化检测的影响。采用以上方法检测到轴承退化后,在后续的状态监测过程中,根据轴承振动信号预测轴承的剩余寿命,从而为轴承的维护维修提供参考。
2.2 退化模型
轴承的退化模型是用来描述轴承健康状态与其工作时间关系的数学模型。由于RMS描述的是信号强度,能够反应轴承整体损伤,对于轴承的故障发展程度较为敏感。因此,当使用2.1节中方法检测到轴承退化后,采用RMS来表征轴承的故障发展程度。RMS是一个有量纲参数,会受到负载、安装等工况的影响,因而容易引发错误的预测结果。为了降低这一影响,利用相对RMS值(Relative Root Mean Square,RRMS)作为健康指标,用于轴承剩余寿命预测。RRMS的具体定义为
(10)
式中:XRRMS(t)为信号采集时刻t的RRMS值;XRMS(t)为该时刻的RMS绝对数值;XRMS(FPTl)为轴承剩余寿命预测起始点的RMS绝对数值。
通常,机械设备的退化过程是一个随机过程。机械设备随机退化过程的不确定性主要来源于四个方面:①临时不确定度;②单元-单元不确定度;③非线性不确定度;④测量不确定度。Si的研究中提出了一种包含前三种不确定度的自适应退化模型。结合该模型与轴承的退化特点,建立轴承的退化模型为
X(t)=a+λtb+σB(t)
(11)
式中:X(t)为时刻t的RRMS值;a为系统的初始状态,通常等于0;λ为时变参数,代表系统的退化速度;b为系统的非线性度;σB(t)为服从正太分布N(0,σ2)的布朗运动。
在轴承的状态监测过程中,很难准确地对轴承的运行状态进行测量,因而采用振动信号这种间接测量方式反应其健康状态,但间接测量结果与其真实状态间存在一定的误差。同时,信号处理与特征提取过程中都会产生一定的误差。因此,得到的特征与轴承的真实状态之间存在误差,这些误差统一作为测量噪声。因而建立轴承的测量方程为
Y(t)=X(t)+ν
(12)
式中:ν为轴承的测量噪声,服从正太分布N(0,γ2)。
由于工作环境和材料参数等各方面的原因,每个轴承的参数λ,b取值均不相同。为了准确地预测轴承剩余寿命,必须准确地估计各个参数的值。根据轴承的退化模型,可以得到其状态转移方程和测量方程
(13)
式中:η=σ(B(tt)-B(tt-1))服从正太分布N(0,σ2Δt),Δt=tt-tt-1。
2.3 剩余寿命预测
轴承退化模型确定后,便可以通过1.2节所述的UPF算法步骤利用测量值对模型参数进行更新,得到测量时刻t的模型参数,并估计此时的退化状态。利用退化模型传递现有分布,可以预测t+p时刻的状态。在PF算法中,一种比较简单的预测方法就是计算每个粒子在t+p时刻的状态,从而得到系统的状态。
(14)
假设t时刻得到的粒子能够准确地表示t时刻的系统状态,则可以通过递推的方式,最终得到t+p时刻的状态。递推公式为
(15)

3 案例分析
为了阐述提出方法的有效性,采用实际试验中得到的全寿命周期振动信号对提出方法进行验证。并将提出方法与传统PF方法进行对比,说明提出方法的优越性。
3.1 试验台与试验数据
本文所采用的数据由FEMTO-ST机构提供,该数据曾用于2012年寿命预测与健康管理数据挑战[16]。采集该数据的试验平台如图2所示。通过加速性能退化技术,该试验系统能够在较短时间内收集轴承的全寿命周期数据。试验中,轴承振动信号的采样频率为25.6 kHz,数据长度为2 560,每隔10 s采集一次。试验中,分别采集了横向和垂向的振动信号。但试验过程中施加的力为径向力,因此,横向振动信号更能反映轴承的工作状态。因此,本文选用横向振动信号进行分析,从横向振动信号中提取特征表征轴承的健康状况。

图2 加速寿命试验台Fig.2 Overview of the experimental platform
图3为一个典型的轴承全寿命周期振动信号。由图可以看出,轴承经历了一段较长的正常工作时间,然后开始退化,一旦开始退化后,轴承的性能迅速退化直至失效。

图3 轴承振动信号Fig.3 The vibration signal of a bearing
3.2 轴承剩余寿命预测
本文提出的方法需要先判断其是否进入退化阶段,即找出第一个剩余寿命预测点,然后再对轴承进行剩余寿命预测。根据第2部分所述方法,提取轴承振动信号的峭度值与RMS,如图4与图5所示。首先,根据2.1节所述方法,利用峭度值判断轴承退化起始点。由图4可知,当轴承正常工作时,峭度值比较稳定,同时由于随机噪声的存在,这个过程中也会出现异常值。采用2.1节中所述触发机制消除随机噪声的影响,结果表明,当t=10 910 s时,轴承开始退化,如图4中的竖线所示。因此,选择t=10 910 s为轴承的第一个剩余寿命预测点。相应地,图5中的竖线表示轴承的退化起始点,此时轴承的RMS值变化较大,此后RMS值一直随着退化程度的加深而增大。

图4 轴承振动信号的峭度值Fig.4 Kurtosis results

图5 轴承振动信号的RMS值Fig.5 RMS results
检测到轴承开始退化后,计算每一个信号采集时刻的RRMS值,利用2.2节与2.3节所述方法完成轴承的剩余寿命预测。图6为退化模型参数的更新过程,图中横坐标0 s表示第一个剩余寿命预测点,后续横坐标值均表示当前时刻距离第一个剩余寿命预测点的时间,图7、图8、图9以及图10中横坐标的意义均与图6一样。由图可知,刚开始进行参数估计的时候,由于涉及的测量信息较少,参数估计结果存在较大误差。随着测量数据的增多,参数λ与参数b均逐渐收敛于真实值。因此,采用本文提出方法能够有效地利用测量数据估计退化模型参数。
为了说明本文提出方法的有效性,将PF方法作为对比。分别利用两种方法对轴承退化阶段的状态进行追踪,得到的结果如图7所示。由图可知,PF方法和UPF方法都能够准确地追踪RRMS值,在少数点处,UPF的估计结果比PF的估计结果更为准确。

图6 退化模型参数更新过程Fig.6 Update process of model parameters

图7 轴承退化过程中RRMS估计值Fig.7 RRMS estimations of bearing degradation process
为了验证相对于PF方法,UPF方法能够有效解决粒子退化问题,采用有效粒子数来衡量状态更新过程中粒子的退化程度[17]。状态估计过程中,两种方法所选择的粒子数均为1 000,整个过程中,两种方法的有效粒子数如图8所示。由图可以看出,迭代开始后,两种方法的粒子均迅速退化,但整个过程中,UPF方法的有效粒子数始终大于PF方法的有效粒子数。
为了验证UPF方法在寿命预测中的作用,选用第10个时间点和第35个时间点的预测结果来说明UPF方法相对于PF方法的优越性。图9为已知10组数据时的预测结果,由图可以看出与PF方法相比,UPF的预测误差较小。已知10组数据时,使用PF方法预测到RRMS值超过失效阈值的时间为580 s,而真实的失效时间为490 s,因此,其剩余寿命预测误差为90 s。而当使用UPF方法时,预测到RRMS值超过失效阈值的时间为520 s,其预测误差为30 s。图10为已知35组数据时的预测结果,由图10可知,随着测量值的增加,两种预测方法的准确度都随之增加。但UPF方法的预测结果依然比PF方法好,此时,PF预测方法预测轴承的失效时间为520 s,预测误差为30 s,而UPF方法预测轴承失效时间为480 s,预测误差为10 s。UPF方法的预测误差低于PF方法的原因可以解释如下:在UPF方法中,每个粒子均采用UKF方法进行了更新,因而不会与实际状态产生很大的偏差。在后续权值更新过程中,由于其与测量值相差不会过大,因而避免了大部分粒子权值过小发生退化,能够更好地估计系统状态。因此,UPF方法能够有效解决PF方法中的粒子退化问题,提高轴承剩余寿命预测的准确度。
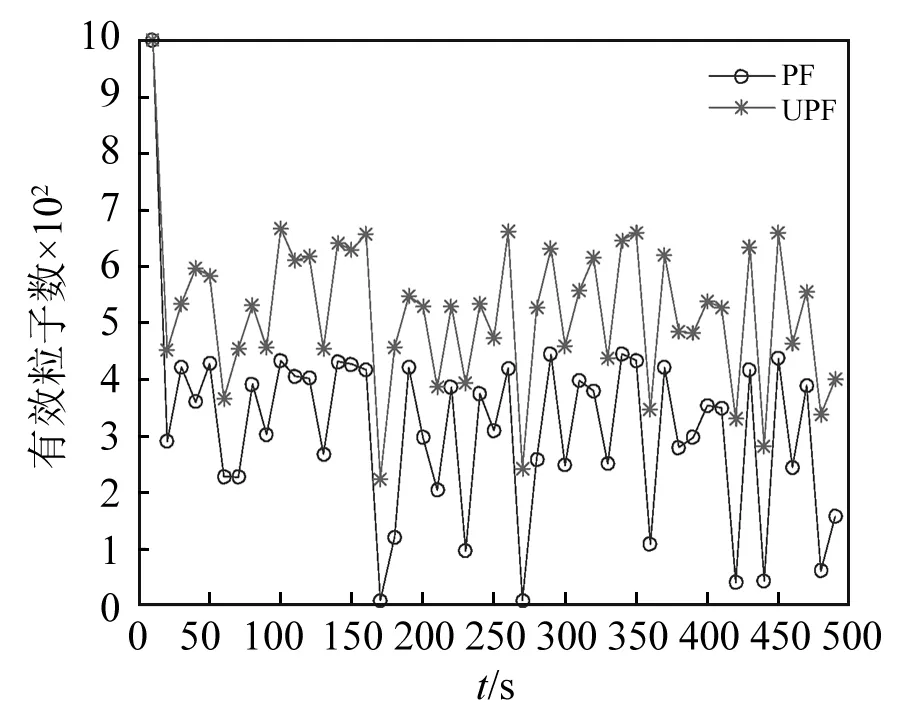
图8 有效粒子数对比Fig.8 Comparison of the effective sample sizes

图9 10组数据时的预测结果Fig.9 Prediction results with 10 measurements

图10 35组数据时的预测结果Fig.10 Prediction results with 35 measurements
4 结 论
PF算法是一种广泛用于解决目标追踪问题的方法。近年来,PF技术被引入剩余寿命预测领域。但随着迭代次数的增加,PF算法会出现粒子退化问题。UPF算法结合PF和UKF,能够有效解决这一问题。本文提出了一种基于UPF的轴承剩余寿命预测方法,结合随机过程模型与UPF方法,对退化过程中的轴承状态进行追踪,并完成其剩余寿命预测。结果表明,UPF方法能够有效弥补PF方法粒子退化这一缺陷,与传统PF方法相比,本文提出方法能够更加准确地预测轴承的剩余寿命。

