钢箱梁结构在爆炸冲击波作用下局部破坏影响因素试验研究
刘亚玲, 刘玉存, 耿少波, 王万月, 薛建英, 刘 兰
(1.中北大学 理学院,太原 030051; 2.中北大学 化工与环境学院,太原 030051)
斜拉桥、悬索桥是目前大跨径桥梁的主要桥型,钢箱梁是其主要的桥面结构体系。在钢箱梁结构体系中,横隔板、纵隔板及纵肋在垂直方向互相交织,形成网络状承重结构物,与上部的钢板共同称为正交异性钢桥面板。随着桥梁尤其是大跨桥梁遭受恐怖爆炸袭击及其他偶然爆炸的风险日益增大,钢箱梁结构体系作为桥梁结构承受车辆荷载的直接受力构件,其在冲击波荷载作用下的的动力特性和损伤模式,成为研究大跨桥梁抗爆性能的一个重要内容。Suthar等[1-5]利用有限元软件对某桥在爆炸作用下的动力响应和损伤进行非线性研究;Son[6]对缆索支承桥梁钢箱主梁的正交异性桥面板的抗爆影响因素进行了数值仿真分析;白志海[7]对钢箱梁正交异性钢桥面板在恐怖爆炸冲击作用下的塑性变形、开裂与破口进行了数值模拟;朱新明等[8-10]考虑了小轿车和小客车汽车炸弹在桥面不同位置爆炸,分析了爆炸位置和当量对钢箱梁结构破坏模式、响应过程和破坏参数的影响;姚术健等[11]开展了钢箱梁内部爆炸冲击局部破坏机理研究;朱璨等[12]以钢箱梁节段为研究对象,考虑不同爆炸当量的炸药在桥面典型位置处爆炸,分析了钢箱梁、钢筋混凝土主塔的局部破坏特性。
综上所述,对钢箱梁的抗爆研究主要集中在爆炸效应(包括爆炸当量和爆炸位置)对其局部破坏模式的影响上,研究手段都以数值模拟为主,试验研究很少。本文以某缆索支撑梁中钢箱梁结构的一个节段为原型进行缩尺,以汽车炸弹或爆炸物运输车辆在桥面爆炸(忽略冲击波通过运载工具本体的传播)作为爆炸试验设计依据,通过在一定的药量和爆距下改变钢箱梁的结构参数 ,重点研究结构参数对钢箱梁结构破坏特征的影响。
1 试验设计
1.1 钢箱梁缩尺模型设计
本试验中试验试件采用材料力学性能指标见表1。截面形式采用工程中常用的单箱双室和单箱三室结构,如图1所示。试件尺寸的确定根据目前国内连续钢箱梁桥主梁截面的常规设计尺寸[13-14],按照动力相似原则,综合考虑总纵弯曲强度相似及结构形状相似条件,缩尺比例1∶10。各工况试件结构参数见表2。钢箱梁缩尺模型总长度为1 800 mm,两端按固支考虑。U型肋间距为等间距布置或60 mm/30 mm间隔布置,采取矩形封闭式截面或倒梯形封闭式截面。

表1 材料力学性能指标Tab.1 Material parameters

图1 钢箱梁缩尺模型试件横截面图Fig.1 Cross section diagram of the steel box girder scale mode

表2 钢箱梁缩尺模型结构参数Tab.2 Structure parameter of the steel box girder scale model
1.2 试验装置
试验装置如图2所示。钢箱梁两端采用自制的钢架支座固定,钢架支座之间用横梁上下连通,下部用沙袋压实。炸药采用TNT/RDX(40/60)混合炸药,密度为1.597 g/cm3,通过三脚架固定在钢梁的上部。钢箱梁顶板背爆面、加劲肋和横隔板上粘贴有应变片,同时,沿梁跨度1/3和1/4的位置处布置有加速度传感器。采用中北大学自行研制的CJB-V-01壁面型压力传感器对钢箱梁表面空气冲击波超压值进行数据采集,参照小剂量装药战斗部爆炸威力常用测试方法[15-17],超压传感器放置在梁边靠近支座的位置,传感器表面与钢箱梁顶板平齐。

图2 试验装置Fig.2 Experimental devic
1.3 爆炸位置及比例距离的确定
本次爆炸试验选取钢箱梁结构的最不利荷载位置进行研究。对钢箱梁而言,顶板在纵向有U肋和纵隔板的支撑,且支撑数量较多;而在横向,仅有横隔板支撑。作为支撑点较少的横向,横隔板之间的桥面中心是其受力最为薄弱的位置;而对桥梁的主要受力体系而言,炸弹位于横梁中心及立柱附近对受力体系损坏最大。试验中14种工况,有3种工况选在横隔板与纵向腹板交接的位置(即横梁中心,如工况2、工况4和工况14),其余11种工况全部选在两横隔板与纵向加劲肋之间的桥面中心位置进行炸药的布置。
本试验中药柱的药量和悬挂高度参照常用汽车炸弹的TNT当量和底盘距桥面板的距离[18-19],依据爆炸的相似率原则,采用近距离小爆炸来模拟大规模爆炸的破坏特征。
2 试验结果及分析
2.1 钢箱梁表面压力测试
压力是爆炸测量的一个重要参数,是反映结构物遭受空中爆炸攻击时所受外荷载的重要数据,也是爆炸数值仿真计算必须输入的参数。本试验采用中北大学自制的壁面型压力传感器,将传感器固定在如图2所示偏离炸药垂直投影点位置,避免传感器距离爆炸源过近发生损坏。爆炸冲击波入射角φ0=arccot(H/L),大于临界角φc[20](L为传感器距爆心投影直线距离),这样测试所得的压力值可以近视忽略马赫波反射压影响,为间接评定炸药爆炸能量提供试验依据,为后期的数值模拟中炸药参数的确定提供依据。试验所用TNT/RDX(40/60)混合炸药的TNT当量按照其组成成分爆热,依据能量相似原理换算成TNT当量,确定该炸药的TNT当量介于1.2~1.3倍[21],利用文献中理论公式 (考虑到试验中钢箱梁顶板的刚度远小于刚性地面,炸药距离钢箱梁顶板的比例距离小于0.35,所以理论计算采用文献中按普通地面爆炸的冲击波超压公式进行计算)对传感器位置处超压峰值进行了理论计算,并与实测超压值进行了对比,见图3(a)所示。同时,本文利用LS-AUTODYN有限元软件对部分试验工况超压值进行了数值模拟(模拟自由场压力,未建钢箱梁模型)。其中工况3、工况6的超压时程曲线的模拟结果与实测结果如图3(b)和图3(c)所示。从图中可以看出,实测超压曲线的波形相对于自由场压力(数值模拟结果),初始峰压部分更尖更窄。工况6由于顶板开裂,超压实测峰值比模拟值衰减25%,如图3(c)所示。
试验同时发现,超压值的大小与钢箱梁顶板的破坏状态有关。工况1和工况3比例距离和结构参数基本相同,由于材质的原因,工况1顶板出现破口,而工况3顶板破坏状态为凹洞,并未开裂,导致工况1所测超压峰值比工况3衰减38%,如图3(d)所示。图3(a)中也能看出,所有工况中只要钢箱梁顶板出现破口、变形式位移时,所测超压值比理论值衰减很多,衰减最大可达29%,这种衰减,主要原因是顶板开裂、破口损耗了大量的爆炸能量所致。
2.2 钢箱梁顶板破坏状态影响因素及分析
钢箱梁顶板作为直接承受荷载的部位,其受力状态对整个钢箱梁起着非常重要的作用。根据顶板破坏程度的不同,一般分成三大类:塑性大变形(对结构的承载力有一定的影响,破坏程度Ⅰ);局部开裂破口(严重影响结构承载力,破坏程度Ⅱ);完全破坏或断裂(结构丧失承载力,属于整体结构的破坏模式,破坏程度Ⅲ)。试验中发现,在比例距离基本接近的情况下,由于各工况钢箱梁顶板材料、厚度、横隔板间距、加劲肋的厚度间距等因素变化,导致桥面板的破坏状态有很大的不同,具体见表3所示。

注:图中纵坐标0点对应一个标准大气压值图3 超压测结果试对比Fig.3 Comparison of overpressure test results

表3 各工况爆炸位置与破坏情况Tab.3 Position of explosion and damage state
2.2.1材料对破坏状态的影响
如图4所示,工况1和工况7的结构参数除了梁的高度不同之外,其于均相同,比例距离也相同,工况1的材料是冷轧钢板,破坏形态中破口断面呈整齐的切断面,无弯曲变形,顶板有碎片产生,击穿板底;工况7是热轧钢,破口有明显的弯曲变形,两端沿加劲肋边缘撕裂,中间部位下凹,局部裂口;试验同时对比了Q235A和Q235B两种材料的抗爆性能,工况3选用Q235A,工况5选用的是Q235B,其他条件均相同。试验结果两种工况结构破坏形态和破坏范围无明显区别,说明Q235A和Q235B的抗爆性能基本相同。

图4 工况1和工况7的钢箱梁顶板破坏对比图Fig.4 The steel box girder roof breakage contrast Figure for condition 1 and condition 7
2.2.2结构参数对破坏状态影响的理论分析
如图5所示,在14种工况中选取了6个具有代表性的破坏工况。在近距离爆炸作用下,爆炸冲击波只对爆炸点周围有限的部位造成应力集中,塑形区域分布在破口周围的区域,破坏形式有局部塑性大变形(见图5(a)、图5(b))、开裂(见图5(c)、图5(d))、花瓣型破口(见图5(e)、图5(f))。随着药量的增大,破口范围会超越离爆炸点最近区格板的加筋肋和横隔板范围,顶板区格破口严重,加筋肋屈曲失效,如图5(f)。
之所以出现上述不同的破坏状态,除了比例距离,主要是受钢箱梁结构参数的影响。钢箱梁顶板在爆炸载荷作用下产生较大的塑性变形甚至破损,在这种情况下弹性变形可以忽略不计,因而可将桥面板当作刚塑性材料处理。桥面板遭受的爆炸载荷是局部性的,从破坏的状态来看,分为两种情况来分析。

图5 钢箱梁顶板典型破坏状态对比图Fig.5 Comparison of typical damage state of steel box girder roof
(1)桥面板产生局部塑性大变形(冲量荷载小于临界荷载)
如图5(a)、图(b)所示破坏状态。加劲肋和横隔板把桥面板分成了若干个小的区格,冲击波载荷均匀作用在每个区格的上面,从试验结果看,变形主要集中在离炸药最近的区格,因此可以忽略相邻区格的变形,认为爆炸冲击波引起的破坏全部集中到这个区格范围。所以本文单独拿出这个区格进行分析,每个区格的边界可以近似看做是四边固支。该区格的短边为加劲肋的间距,设为a,区格的长边为横隔板的间距,设为b,顶板厚度为δ,尺寸见图6所示。

图6 顶板区格尺寸坐标图Fig.6 Roof area grid coordinates chart
对于钢箱梁,如果将爆炸后结构出现的最大变形及是否出现破损作为研究的主要目的,则可以利用能量法对这一问题进行求解。冲击波对钢箱梁的破坏作用是与超压的正压作用时间t+密切相关的。因为t+远小于钢箱梁本身的振动周期T,即t+< (1) 代入式(1),可以得到 (2) 式中:A为待定系数;Q为炸药量;r为炸药中心距顶板的距离。 此时钢箱梁顶板的变形模式可以参照文献[23-24]中的薄板的塑性大变形理论进行分析,区格板的变形能Up包括弯曲变形的势能U1和相应于中面应变的势能U2,不考虑支座(即加劲肋)的变形。 Up=U1+U2 (3) U1按弯曲变形关系处理,单位体积的弯曲变形势能可以表示为 dU1=σxxdεxx+τxydγxy+τyxdγyx+σyydεyy (4) 其中应变分量满足下列关系式 (5) 式中:ω为所取单元的位移分量,是区格板的关于x和y的挠度函数。 (6) 中面应变的势能U2可表示成 (7) 式中:Nx,Ny,Nxy为中面膜力,其表达式为 Nx=δσxx,Ny=δσyy,Nxy=Nyx=δτxy 板的挠度函数ω可表示为 (8) 式中:B为待定系数,代入固定支座边界条件,假设ω0为区格板中心处的最大挠度,可得ω0=4B。代入式(6)和式(7),最后得到顶板区格的变形能U1和U2的表达式 (9) (10) 此时钢箱梁顶板总的变形能 U=Up (11) 根据能量定理, U=K (12) 由此可以确定区格的最大挠度值ω0,计算结果详见表4所示。将ω0代入式(8)可以求出整个区格板的变形。可以看出,影响区格板塑性变形的主要因素有横隔板间距、加筋肋间距(影响区格尺寸)、材料的屈服强度σs、厚度δ等因素。 表4 各工况试验结果与计算结果比较Tab.4 Relationship between the state of failure and the quantity of explosive (2)桥面板发生开裂、破口(冲量荷载大于于临界荷载) 如图5(c)~图5(f)所示破坏状态。设离炸药最近的顶板上那一点上反射比冲量引起的初始最大速度为υmax,根据动量定理 (13) 钢箱梁顶板破坏时的能量准侧可表示为 (14) (15) 式中:Q*即为钢箱梁顶板开裂破损的最小炸药量。 2.2.3结构参数对破坏状态的试验数据分析 为了进一步比较试验中结构参数在相同比例距离下对钢箱梁顶板的局部破坏程度的影响,本文引入了破坏程度指数Ω,定义如下 (16) 图7 顶板厚度对钢箱梁破坏状态影响Fig.7 The impact of roof thickness on the failure state of steel box girder 图8 加劲肋加劲肋系数和上口间距对钢箱梁破坏状态影响Fig.8 The influence of stiffening rib spacing and stiffening rib coefficient on the failure state of steel box girder (1)超压值的大小与钢箱梁顶板的破坏状态有关,钢箱梁顶板出现破口、变形式位移时,所测超压值比理论值会衰减很多。 (2)在近距离爆炸作用下,爆炸冲击波只对爆炸点周围有限的部位造成应力集中,而对其他位置的应力较小,塑形区域只分布在破口周围的区域,在药量增大的情况下,破口范围会超越加劲肋和横隔板,加筋肋屈曲失效。 (3)用能量法可以很好的预测近距离爆炸作用下钢箱梁顶板的破坏状态及估算顶板发生塑性变形的挠度和发生开裂等的能量损耗值得大小。 (4)破坏状态与破坏程度是一个多参数共同影响的综合结果。从试验结果来看,顶板厚度、U肋、横隔板间距等参数可以提高钢箱梁顶板的抗爆能力,尤其是U肋的约束作用尤为显著(破坏程度的降低幅度达到80%以上)。
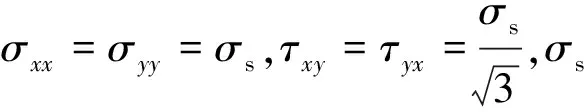







3 结 论

