一类静电驱动双边电容型微谐振器振动系统的复杂动力学特性研究

尚慧琳， 胡立力， 文永蓬

(1. 上海应用技术大学 机械工程学院，上海 201418；2. 上海工程技术大学 城市轨道交通学院，上海 201620)

静电微谐振器是微机电系统(Micro-Electro Mechanical System, MEMS)的重要器件,是目前发展最快的MEMS产品之一，是以谐振原理实现功能的典型微器件[1]。然而，静电微谐振器在应用中存在着多种复杂动力学现象，不仅包括宏观机械振动系统中常见的振动跳跃、概周期振动、多倍周期振动和混沌等，还包括静电驱动微器件所特有的吸合不稳定[2]。随着MEMS的广泛应用，微谐振器的稳定性和可靠性对其振动系统和动力学特性的研究提出了更高的要求。因此，研究静电驱动微谐振器的复杂动力学特性及其机制对于静电微惯性传感器的研发具有重要的现实意义。

目前，国内外大量数值和试验研究结果表明静电微谐振器振动系统普遍存在谐振失稳行为(如振动跳跃现象[3-4]、概周期振动[5]和倍周期振动[6]等)、发散失稳行为(如吸合现象)和全局失稳行为(如混沌现象[7-9]和吸合不稳定现象)。其中，吸合现象是近年来MEMS领域的研究热点[10]；与之相关的吸合不稳定，即一定的设计参数条件下初始条件的微小变化就导致微结构从原本的不吸合变为吸合的现象，会大大降低微器件的安全性，正逐渐引起国内外研究者的研究兴趣[11-13]。Luo等发现在一类双边电容型微谐振器振动系统中交流电压频率的变化会引起混沌。Ruzziconi等在另一类静电微谐振器振动系统中交流电压频率的变化引起的多稳态现象和振动跳跃。Zhang等发现压膜阻尼非线性引起的多倍周期振动、概周期振动和混沌。对于以上复杂动力学现象的研究，数值仿真占主要比重，其中对于吸合不稳定和振动跳跃是通过初始状态的微调引起稳态响应的突变来模拟现象的，该量化研究方法由Lenci等和Ruzziconi等分别提出，利用振动系统的安全域侵蚀程度和各稳态解的吸引域分形程度来描述这两类破坏系统的动完整性的动力学行为。尚慧琳等[14]在此基础上以一类静电驱动单边电容型微谐振传感器为研究对象，基于安全域思想研究了系统直流偏置电压和交流激励电压幅值引起的结构吸合不稳定现象。尽管这些复杂动力学行为的存在性和其对于微器件性能的影响已受到MEMS设计者和研究者的关注，其机制仍未得到广泛地理解。

基于上述原因，本文对一类典型的双边电容型微谐振器的动力学模型进行了分析，通过了解其静态分岔、局部分岔和全局分岔动力学特性，研究该系统的复杂动力学行为的机制，从而为诱发、控制和避免静电驱动微器件结构的复杂振动提供一定的理论依据。

1 动力学模型

1.1 无量纲化系统

考虑一类两侧平行板电容、在直流偏置电压和交流电压驱动下静电驱动的微传感器振动模型[15-16],如图1所示。考虑线性刚度、非线性刚度、线性阻尼和非线性激励，建立振动方程

(1)

式中：x为微结构的位移；m为微结构等效质量；c,k1,k2分别为系统的等效阻尼系数、线性刚度和非线性刚度；A0为平行板初始静止时的电容；d为极板初始间距；Vb,VAC分别为直流偏置电压和交流电压的值，且VAC≪Vb；Ω为交流电压的频率。

图1 一类静电驱动两侧平行板电容微传感器振动系统简化模型Fig.1 Diagram of the dynamical system of a typical a micromechanical resonator with electrostatic forces on both sides

为了方便表述，对微传感器振动系统式(1)引入以下无量纲变量

(2)

则可知|u|≤1得到以下无量纲化模型

(3)

下文的研究将围绕式(1)的无量纲化系统式(3)开展。对式(3)重新标度参数，即

(4)

则有

(5)

1.2 无扰动系统分析

重新标度过的无量纲化系统式(5)的无扰动系统为

(6)

这是一个哈密顿系统，其哈密顿量为

(7)

设零平衡点处势能为0，则相应的势能函数可表示为

(8)

根据式(6)～式(8)，系统的平衡点个数，有无势阱，以及势阱的具体位置和形态均取决于参数α和β。由于无量纲化参数α与驱动电压无关，而β是直流偏置电压的函数，因此系统的平衡点个数与交流电压无关，却与直流偏置电压有直接关系。

定理1 如果参数满足

(9)

则式(6)只有一个零平衡点，为鞍点。

证明：令

(10)

(11)

G′(u)=0无解, 当u∈(-1, 1)始终有G′(u)>0。考虑G(u)的单调性，G(u)=0无解, 式(6)没有非零解。

当

(12)

(13)

这说明当u∈(-1, 1)时G(u)始终大于零，G(u)=0在该区域无解。

因此，当式(11)或式(12)满足时，即式(9)满足，则式(6)只有一个零平衡点，由于其对应的特征方程

l2-(4b-1)=0

具有一正一负两个实根，因此零平衡点为鞍点。证毕。

由此可见，当β充分大的时候，系统无非零平衡点和势阱，系统将不可避免地出现无界振动，这意味着图1的动极板将直接吸合到定极板上，即发生静态吸合。而微结构间的吸合现象则会导致静电微谐振器件的失效，这是微结构中值得关注的重要现象。由于质量m、刚度k1,k2、极板初始间距d和平行板初始静止时的电容A0等设计参数对于微谐振器是给定的，将不等式(9)还原成微结构振动系统式(1)的物理参数，得到

(14)

给定参数α，改变β，无扰动系统式(6)的势能分布情况如图2所示。根据图2中势能曲线的极点分布可知，β=0.25时系统有3个平衡点，其中两个非零平衡点不稳定，而零平衡点为中心，因此具有单势阱和异宿轨道；β=0.338时系统有5个平衡点，其中O(0,0)，S1(-0.768 996,0)，S2(0.768 996,0)这3个平衡点均不稳定，而中间两个非零平衡点C1(-0.196 339,0)和C2(0.196 339,0)为中心，因此系统具有双势阱、同宿和异宿轨道，其中根据其哈密顿量式(7), 同宿轨道可近似表示为

外面的异宿轨道可表示为

(15)

式中：us=0.768 996为鞍点S2的横坐标，相应的无扰动系统相轨线如图3所示；当β增大到0.6时，定理1条件满足，系统只有一个零平衡点，体现为鞍点。

图2 在α=12,β取不同数值下的势能图Fig.2 The potential energy in the phase portrait underα=12 and different values of β

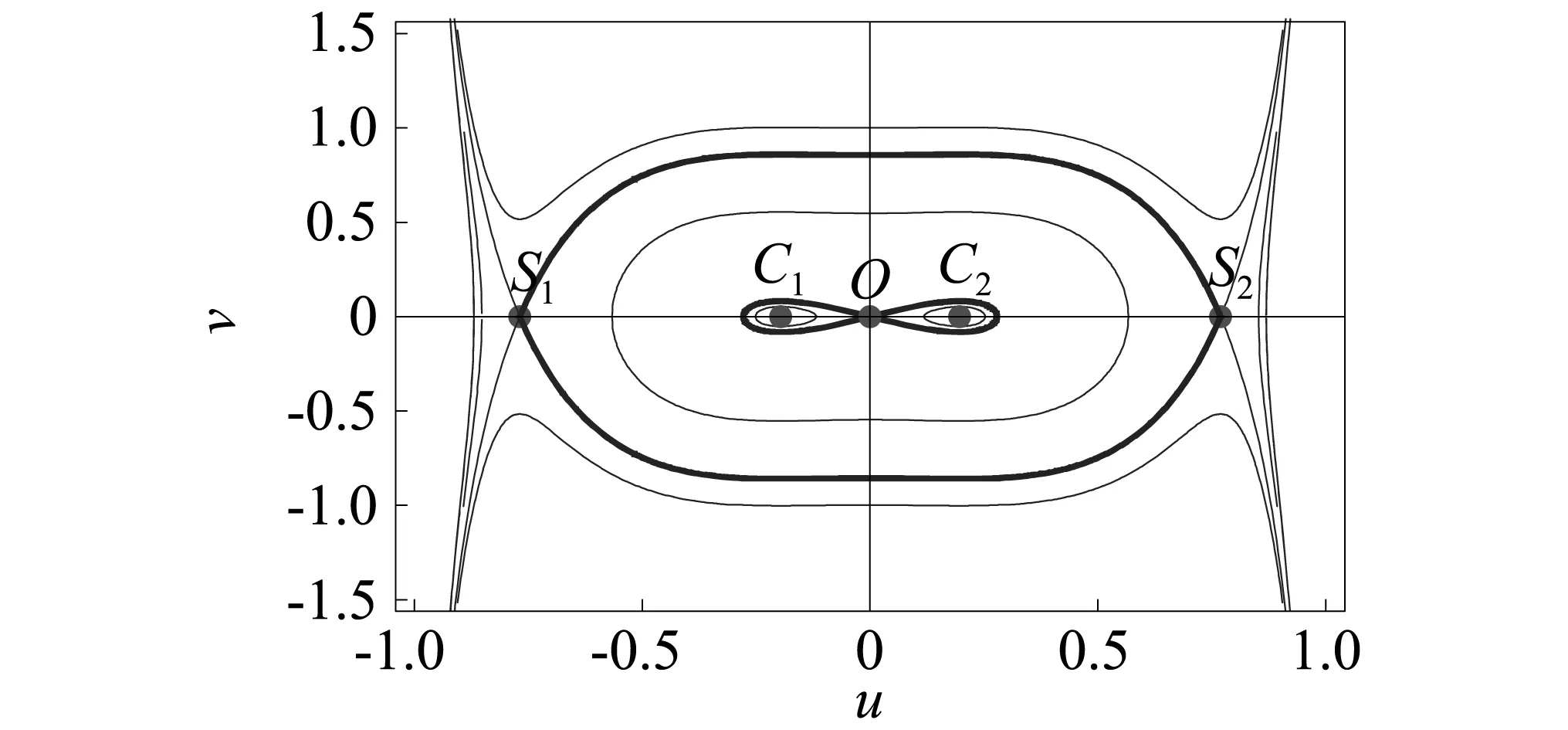
图3 当(α,β)=(12,0.338)时相轨线分布Fig.3 Trajectories in the phase portrait when (α,β)=(12,0.338)

以上3种情况当中，β=0.338这种情况最为复杂，这也是双侧极板电容微谐振器比较常见的设计参数取值，对应的系统设计参数取值如表1所示，由于无扰动系统存在多势阱的情况，仍会出现部分初始条件导致微结构的吸合；而另一部分则不会引起微结构吸合，该部分的集合则可称为安全域。安全域的分形侵蚀意味着微结构的吸合不稳定。以下本文重点讨论该参数条件下微结构包括吸合不稳定现象在内的复杂动力学行为及其机制。

表1 式(1)的物理参数值Tab.1 Values of physical parameters of the equation (1)

2 多稳态运动分析

对于微结构振动系统式(1)及其无量纲化系统式(5)，当驱动交流电压VAC为0时，根据Jacobi矩阵求解特征值可知，非零平衡点(±0.196 339,0)为稳定平衡点，这是系统最初的双稳态现象。当驱动交流电压幅值开始升高时，该非零平衡点失稳，开始出现周期振动，以下将对周期振动特性进行具体分析。

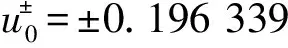
(16)

对式(16)将分母泰勒展开,省略ε和u三次方以上高阶项，简化得到

(17)

为了运用多尺度方法，对参数和时间重新标度

(18)

代入式(17)，对比三阶系数

(19a)

(19b)

(19c)

(20)

代入式(19c)，得到

(21)

(22)

和

(23)

图4 当ω=0.5时无量纲化系统式(3)周期解支分布Fig.4 Brunches of periodic solutions ofthe dimensionless system (3) when ω=0.5

图5 当ω=0.5时无量纲化系统式(3)的多稳态解Fig.5 Multistability of the dimensionless system (3)when ω=0.5

3 混沌和吸合不稳定

图6 初始条件时无量纲化系统式(3)响应随VAC的分岔Fig.6 The bifurcation of the oscillation ofthe dimensionless system (3) with VACunder the initial condition 0)

图7 当VAC=0.2 V, ω=0.5时无量纲化系统式(3)的相图和庞加莱截面图Fig.7 The phase map and Poincare map ofthe dimensionless system (3)when VAC=0.2 V and ω=0.5

由于考虑系统的长期行为，因此设定系统振动在105个参数激励周期内均满足|u|<1，则认为相应的初始条件下系统不发生吸合现象，该初始点在初始平面中用黑色标记；否则则发散失稳，用白色标记。取初始点的个数为200×200。激励周期的数值积分步长为10-4。式(3)的安全域随交流电压幅值的变化规律如图8所示。由图8可知，随着交流电压幅值的增大，系统的安全域逐渐出现分形侵蚀，对应微结构的吸合不稳定，当驱动交流电压幅值增大到1 V时，整个初始平面不存在安全区域，即所有初始条件均会导致微结构吸合，这意味着微结构又回归静态吸合。同时，结合图6～图8，可以观察到发生吸合不稳定和混沌运动所对应的驱动交流电压幅值并不相同：系统在驱动交流电压幅值为0.2 V时出现混沌现象，此时安全域边界并未发生分形侵蚀，这说明吸合不稳定和混沌现象并不同步发生。Haghighi等已将本系统混沌运动归因于同宿轨道的破裂，并分析了同宿分岔的临界条件。吸合不稳定与混沌现象的不同步意味着吸合不稳定这类全局动力学问题并不能同样归因于同宿分岔，反而对比图3中的无扰动系统的异宿轨道和图8(a)中驱动交流电压为0的安全域可发现二者高度吻合。以下对标度过的无量纲化系统式(5)运用Melnikov方法来预测异宿分岔的必要条件，并加以对比。由于异宿轨线式(15)与近似同宿轨道不同，并不是时间T的显函数可，根据式(15)将时间T表示为u的函数

(24)

忽略式(5)中ε三次方以上高阶项，将其它含ε的项当作摄动项，得到系统的Melnikov函数

其中，

(25)

图8 ω=0.5时无量纲化系统式(3)安全域随驱动交流电压的演变Fig.8 The evolution of safe basin ofthe dimensionless system (3)with the amplitude of AC voltage when ω=0.5

4 结 论

本文考虑一个双边电容静电驱动微谐振器结构振动系统，应用分岔理论和数值模拟方法分析了驱动电压引起的静态吸合、振动跳跃、多稳态运动、混沌和吸合不稳定等复杂动力学特性，为静电驱动微谐振器的设计中如何避免复杂响应提供参考。主要得到以下结论：

(1)直流偏置电压的增大容易直接导致微结构的静态吸合，为抑制该现象，直流偏置电压应低于文中给出的直流电压静态吸合阈值。

(2)在较小的直流偏置电压下，交流电压幅值的增大会陆续引起微结构的振动跳跃现象和多倍周期振动现象，混沌、吸合不稳定和最终的吸合；为了避免振动跳跃现象和吸合现象的发生，选取的系统初始条件应靠近两个非零平衡点(即交流电压为零时的两个点吸引子)，且保持较低的交流电压幅值；而当交流电压幅值增大到一定程度，无论系统初始状态如何选取，微结构都不可避免地发生吸合现象。

(3)混沌和吸合不稳定这两类破坏振动系统的动完整性的动力学现象并不同步发生，尽管二者均可归因为系统的全局分岔，但机理并不相同。