正交各向异性薄板振动响应的波函数法

赖诗洋， 夏小均， 徐中明

(1. 重庆工程职业技术学院 机械工程学院,重庆 402260; 2. 重庆车辆检测研究院有限公司，重庆 401122；3. 重庆大学 汽车工程学院,重庆 400030)

现阶段发展较为成熟的有限元方法主要应用于低频[1-2]，统计类方法只在高模态重叠率的前提下成立[3]，两者在中频振动噪声分析中具有一定的局限性，而混合FE-SEA方法[4-6]建模过程所需参数较多且无法得到模型的细节。在确定性的中频预测方法研究[7-9]中，由Desmet[10]提出的波函数法具有高效、高精度、自由度少的特性，是一种确定性的Trefftz法[11-12]，能够解决有限元方法、统计类方法在中频声振分析中的不足。目前，该方法已经成功运用到了各向同性薄板的弯曲振动[13-14]、各向同性厚板的弯曲振动[15]、结构声学耦合响应[16-17]、多孔阻尼材料声学耦合响应[18]等问题中。

随着材料科学的发展和工业上对结构性能要求的提高，越来越多的复合材料被用于替换传统结构材料，像蜂窝板、纤维增强聚合物等都已经运用于航空、航天、船舶和汽车工业。而且这类典型的结构声耦合系统在采用正交各向异性的薄板时，由于其在不同方向上具有性质不同，原有的各向同性薄板理论已不适用[19]，其振动响应特性的改变将很大程度上影响产品的NVH性能，采用波函数法可快速准确地对正交各向异性薄板的振动响应进行预测。因此，对正交各向异性薄板，采用波函数法实现在更高频段的振动响应预测，进一步为产品设计优化提供必要的指导，有着重要的实际工程价值和意义。

文章基于正交各向异性薄板的弯曲振动与波函数法理论，推导了能描述正交各向异性薄板振动响应的结构波函数，建立了正交各向异性薄板在外部作用下的响应模型，再结合加权余量法实现波函数法对正交各向异性薄板的振动响应预测，并通过数值算例验证了方法的正确与高效性。

1 正交各向薄板弯曲振动

对于薄板，以Kirchhoff理论为基础对正交各向异性板的振动特性进行分析。设其弹性主轴平行于x,y方向的正交各向异性板，则在外部激励f(x,y,t)下的法向振动位移响应控制方程为[20]

(1)

其中正交各向板的参数定义为

式中:E1，E2和v1,v2分别为沿x,y方向的弹性模量和泊松比;G为xy平面的剪切模量；ρ为平板材料密度；h为薄板厚度。

在圆频率为ω的简谐激励f(x,y,t)=F(x,y)e-iωt下，正交各向薄板的稳态响应为

ρhω2w=F

(2)

该式为4阶微分方程，要获得薄板的法向振动位移响应w，则至少需要确定两类结构边界条件。与各向同性板类似，其常用的边界条件也包括运动学边界、力学边界和混合边界。

运动学边界

(3)

力学边界

(4)

混合边界

(5)

转角

(6)

弯矩

(7)

等效剪切力

(8)

2 正交各向异性薄板作用力响应

外部激励作用于正交各向异性薄板时，由于薄板的材料特征与各向同性材料已经不同，得到的响应也会不一样。因此，对于此类材料薄板，在外部激励下的振动位移响应，成为求解薄板全局弯曲振动响应的关键。考虑集中力的情况下，在平板的垂直法向作用一简谐力于(x0,y0)，则有

f(x,y,t)=Fe-iωtδ(x-x0)δ(y-y0)

(9)

则控制方程式(2)可表达为

ρhω2w=Fδ(x-x0)δ(y-y0)

(10)

运用二维傅里叶变换将w(x,y)转化为波数域(kx,ky)有

(11)

相应的逆变换为

(12)

将上式的积分变量(kx,ky)转换为(k,a)的函数kx=kcos(a),ky=ksin(a)。由于是对角度进行积分，将笛卡尔坐标(x,y)转换到柱坐标(r,θ)下有x=rcos(θ),y=rsin(θ)。由于响应以2π为周期的积分，将式(12)按cos(a-θ)>0和cos(a-θ)≤0进行分段积分，相应的积分区间为0-π/2～θ+3π/2，得到无限正交各向异性板在点激励下的响应为[21-22]

(13)

式中：kf(a)为定义的角坐标下弯曲波数。

(14)

G(a)=D11cos(a)4+2(D12+2D66)cos(a)2sin(a)2+

D22sin(a)4

(15)

为体现正交各向异性板在点激励下的响应特性，现取尺寸为(0.4 m×0.4 m)的方形石墨-环氧薄板，其主轴与x,y方向平行,材料参数为E11=138 GPa，E22=8.9 GPa，G12=5.176 GPa，v12=0.3，ρ=1 600 kg/m3，h=0.005 m。在其正中位置施加单位力，计算该薄板的法向位移响应，结果如图1所示，可知正交各向异性板的位移响应不再如各向同性板响应是圆形的轴对称云图，而是根据各主轴弹性模量的变化而变化。

图1 各向异性板振动位移响应Fig.1 Displacement response of an orthotropic plate

3 正交各向异性薄板波函数法

波函数法是一种完全不同于单元类方法的确定性数值分析手段。该方法是将分析域变量表示为严格满足控制方程的一系列波函数的叠加，再通过加权余量法实现边界残差积分归零来求得各波函数的权系数，进而得到全局响应。

基于波函数法理论，正交各向异性板的法向振动位移w可表示为一系列波函数φs的叠加

(16)

3.1 正交各向异性材料波函数

由式(16)可以发现要求得正交各向异性材料薄板的弯曲振动响应，前提是得到精确满足齐次控制方程的结构波函数。采用类似各向同性材料薄板的波函数形式，而由于正交各向异性材料各主轴参数的不同，对应x和y方向的波数定义也将不同。

(17)

式中：nb=4(ns1+1)+4(ns2+1)为模型自由度，也即计算成本的反映。

将定义的波函数形式代入式(2)的齐次方程中得到

(18)

式中:Lx,Ly为薄板在x,y方向的外轮廓尺寸。

依据波函数法理论，求解变量在波函数取无穷数量时才能得到精确解。实际中需要一定的截断准则，该准则是要求最高频率下波数满足描述实际物理尺寸的振荡特性。定义截断系数T(≥2)，满足如下规则

(19)

3.2 边界积分

类似于各向同性板的波函数法，板的响应由各波函数叠加得到，且各波函数的权系数仍由边界积分得到。运用Galerkin加权余量法使板的各边残差为零，有

(20)

将各边界余量值Rw，Rθ，RM，RV代入式(20),得到包含各波函数权系数ws的系统矩阵如式(21)，求解该矩阵，再将获得的波函数系数代入式(16)，便可求解得到正交各向异性薄板的弯曲振动响应。

[A]{ws}={f}

(21)

其中,

(22)

4 数值验证

为了验证论述方法的正确性，引入单向纤维聚合矩形薄板，结构尺寸如图2所示，材料参数如表1所示，分析其在周边简支与周边固支情况下的法向振动响应。板的厚度为1 mm，在板(xq,yq)=(0.16 m,0.14 m) 处作用一法向单位力，并设定点(0.46 m,0.3 m)为参考响应点。波函数法模型的建模与求解都在matlab平台，且截断系数T=6。为了对比，该薄板振动响应也以有限元软件MSC/Nastran2012进行分析。为了保证有限元法的精度，采用了尺寸为4 mm的四边形壳单元进行建模，且采用了直接求解方式。

图2 正交各向异性板Fig.2 Problem geometry of orthotropic plate

表1 复合材料参数Tab.1 Mechanical properties of orthotropic materials

4.1 简支边界

对于边界为周边简支的薄板在200 Hz的响应如图3所示。结果表明，波函数法结果与精细建模的有限元结果一致。由薄板在单位力的位移响应方程可以看出，由于激励点位置距离过小，造成了特解方程在此点奇异，其值是运用附近点拟合求得，因此该点与有限元法的计算结果存在一定差异。

图3 简支边界正交各向薄板200 Hz振动响应Fig.3 Displacement of orthotropic plate with simply supported boundary at 200 Hz

同时，对于四边简支的正交各向异性板，可以双级数的形式加以描述[23]，并以此进一步验证波函数法的正确性。

(24)

其中，

式中：m，n分别为x,y方向半正弦波的波数，本文中m=n=50。

图4为选择参考点R在1～1 000 Hz的振动响应位移曲线。为对波函数法进行充分的验证，该点的响应以双级数法、有限元法(精细网格)与波函数法进行计算与对比。从图中可以看出，三种方法得到的结果吻合较好，也验证了基于波函数法对正交各向异性板在简支边界下的正确性。

图4 简支边界下参考点的频响对比曲线Fig.4 Frequency response of reference point R with simply supported boundary

4.2 固支边界

对于周边固支的薄板，也与成熟的有限元法进行了对比。图5为不同数值方法下得到的薄板在150 Hz时的振动响应位移云图，说明了在固支条件下波函数法计算得到的结果与精细有限元模型得到的结果一致。且参考点在1～1 000 Hz下的响应结果如图6，也验证了该方法对正交各向异性薄板振动响应的有效性。

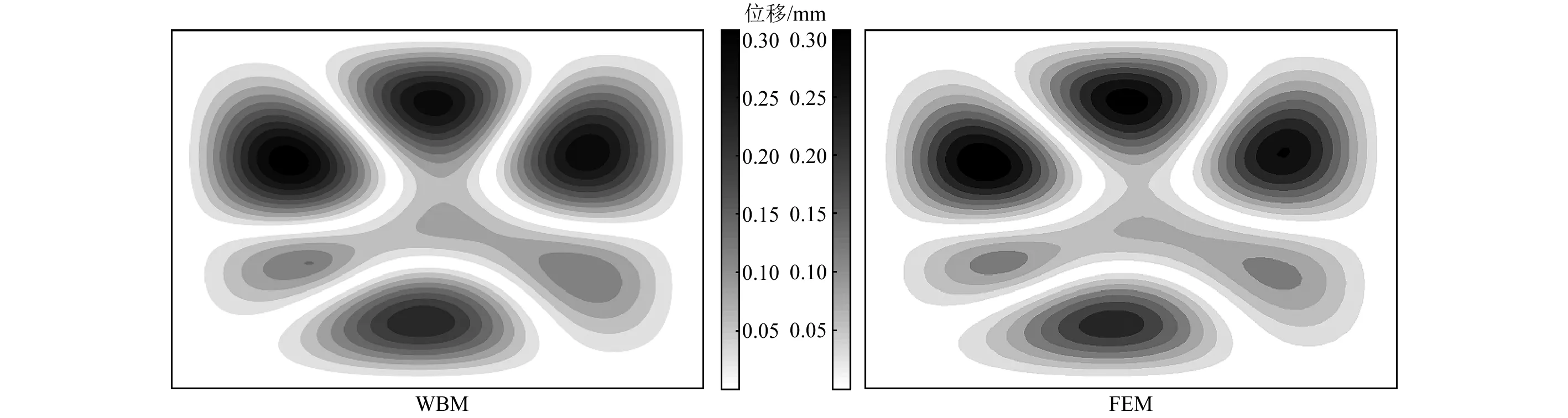
图5 固支边界正交各向异性薄板150 Hz振动响应Fig.5 Displacement of orthotropic plate with clamped boundary at 150 Hz.

图6 R点频率响应曲线Fig.6 Frequency response of reference point R with clamped boundary

4.3 收敛性分析

在波函数法应用于正交各向异性材料时，其计算效率也是反映该数值方法的主要指标。因此，本节对波函数法与有限元法进行比较，分析各自收敛性。通过定义500 Hz时的相对误差来表征计算精度

在同样的计算机配置下(i5-3470,8 G内存)，基于计算时间的收敛曲线如图7所示，尽管波函数法的计算时间包括了模型构建的时间，相对于有限元法计算，仍然有大幅降低。

而模型自由度是其计算量与物理存储的重要表征，直接关系到计算所需的物理内存，因此同时参考何雪松等的研究，以各方法计算自由度为横坐标。图8为波函数法与有限元法在随模型自由度变化下的相对误差曲线，对于正交各向异性材料，相较于有限元法，波函数法仍有着更高的计算效率。

图7 有限元与波函数基于计算时间的收敛曲线对比Fig.7 Comparison of convergence with CPU times

图8 有限元与波函数基于模型自由度的收敛曲线对比Fig.8 Comparison of convergence with degree of freedom

5 结 论

文章运用波函数法对正交各向异性薄板的弯曲振动响应进行了预测分析，得到了能精确描述正交各向异性薄板振动控制方程的结构波函数。基于傅里叶变换推导出了无限正交各向异性薄板在单位激励力的振动幅值响应，再结合加权余量法得到薄板全局响应。引入单向纤维聚合矩形薄板，运用有限元法、级数分析方法和波函数法对其简支边界下的振动响应进行了计算，并以有限元法与波函数法对固支边界下的薄板振动响应进行了计算，两种边界条件下的对比结果都验证了基于波函数法对正交各向异性薄板弯曲振动响应分析的有效性。收敛性分析结果说明，相较于有限元法，波函数法有更高的计算效率，可适用于更高频段振动的预测与分析。下一步将考虑正交各向异性结构的声耦合系统的波函数法响应以及探索针对各向异性材料的波函数法。