不确定通讯下的异构多智能体网络鲁棒编队控制

刘 淼,李忠奎

0 引言

多智能体系统的研究,是近年来系统与控制领域的一个热点.它是一门交叉性学科,涉及到数学、控制、物理、生物、计算机、通信、机器人等学科,受到了众多领域学者的广泛关注[1-4].多智能体系统同步又称多智能体系统的一致性问题,系指根据某种任务要求或性能指标,对单个智能体设计局部控制策略,使得智能体间相互作用,最终使某些感兴趣的状态量趋于一致或相同[5].

多智能体系统同步问题的一个典型的应用就是分布式编队控制[6-12],分布式编队是指若干个智能体在运动过程中组成特定的队形,保持较近的距离,相互协同、共同执行某项特定的任务.与单个个体相比,智能体编队可使每个智能体的功能简化,成本降低,具有一定的冗余度.实现分布式编队的方法之一是利用邻居智能体的相对位置向量构造控制器,这通过简单的线性变换可以化为一致性问题[6].文献[7]对于积分器类型的多智能体系统,提出了基于一致性算法的分布式编队控制器.文献[8]提出了一个解决多车辆系统的队形控制问题的理论框架.文献[10]研究了领航者速度未知情况下的网络的分布式编队问题.基于相对位置信息,对各跟随者采用了自适应的控制方法来估计领航者的速度信息.文献[11]考虑了非完整约束的智能体在速度受限的情况下的领航-跟随编队问题,提出了一个基于观测器的动态控制律.

在以上研究多智能体系统的编队控制问题时,通常假设智能体之间以一种理想的方式交换信息.然而在实际中,智能体之间的通信的信道往往存在传输误差和噪声.典型的通信不确定性包括量化精度、丢包、容量限制和传输噪声[14-20].文献[14]研究了同时存在时延和数据传输限制的情况下多智能体系统的平均一致性问题.文献[16]考虑了智能体在获取邻居智能体状态信息时存在测量噪声的情况,通过对相互作用结构的讨论并利用随机微分方程,给出了系统实现均方一致性的充分条件.文献[17]则给出了二阶积分器网络在存在测量噪声情况下的解决平均一致性问题的充要条件.文献[18]研究了多智能体系统一致性问题中的控制协议和通信过程的相互作用机制.文献[19]和[20]则分别研究了对数量化器模型和衰减信道模型,据此文献[15]中提出了包含不确定性的信道模型.在文献[15]中,作者建立了一个具有确定不确定性的通道模型,并提出了在通信通道存在确定不确定性情况下的多智能体系统实现一致性的控制律.一般而言,在智能体动力学模型、通信拓扑和通信通道模型的相互作用下,设计鲁棒一致性协议来实现网络的编队控制是一个很有意义的问题.

在本文中,我们考虑存在通讯不确定性下线性多智能体系统的鲁棒编队控制问题.在文献[15]提出的通道模型的基础上,考虑了通讯存在满足范数有界的不确定性,为了处理各智能体的异构特性,针对每一个智能体,设计了一个分布式的动态补偿器,并得出补偿器的状态可以实现编队的一个基于线性矩阵不等式的充分条件.通过解线性矩阵不等式来设计合适的补偿器参数,使补偿器的状态达到编队控制的目标,随后对每个智能体设计控制器使其跟踪到补偿器的内部状态,从而使整个多智能体系统实现编队控制.本文的贡献主要在对于存在不确定通讯和智能体异构动态特性相互作用下,提出了一种基于动态补偿器的控制方法.随后,我们简单讨论了同构多智能体网络的编队控制方法,给出了实现编队控制的控制律,以及设计方法.

文章的剩余部分安排如下:第1节介绍了一些必要的数学基础和图论知识;第2节描述了本文中的鲁棒编队问题;第3节和第4节分别针对异构和同构两种情况,给出了存在不确定性通讯情况下的编队实现方法;第5节给出了一个仿真实例;最后,第6节总结了全文.

1 数学基础和图论

1.1 数学基础

引理1(Shur补引理):对任意矩阵

下面几个命题等价:

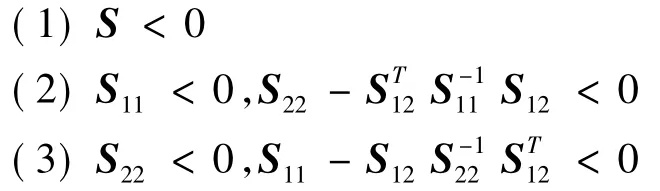
引理2:对任意的实对称矩阵R和矩阵X和Z,下列命题成立:

对所有的矩阵 Y满足 YTY0满足:

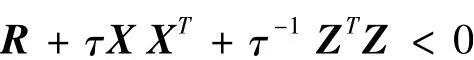
1.2 图论

研究多智能系统使用的数学工具很多,其中代数图论是其中最基本的一种.在做数学建模时可以用图及其拓扑结构来形象地描述各智能体之间信息交互的行为及系统的其他重要的性质.通过图论的相关知识,我们可以将多智能体系统网络中各个智能体间的关系用一个图形象的表示出来,并结合矩阵知识进行处理.本节简要介绍了图的基本概念及其矩阵表达,主要参考了文献[21][22].

由邻接矩阵和输出度矩阵,可以构造图的拉普拉斯矩阵L,也可表示为:

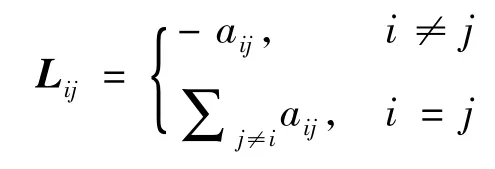
其中Lij对应为拉普拉斯矩阵L的第 i行第j列的元素.由拉普拉斯矩阵的定义,不难发现拉普拉斯矩阵的每一行元素的和均为0.所以,L总是具有一个零特征值λ1=0对应的一个右特征向量是1,即[1,…,1]T.因为1属于L的零空间.因此满足L1=0.对于一个无向图G,在给图中的每条边分配一个任意的方向后,每一条边因此有了头部和尾部,可以定义关联矩阵D=[dij]∈R|v|X|ε|.当节点vi是边(vi,vj)的头部时取dij=1,为尾部时则取dij=-1,其余情况取0.利用这个关联矩阵,有如下引理:

引理3:对于一个无向图 G,L=DWDT其中W∈R|ε|X|ε|为各个边的权值形成的对角阵.

2 问题描述

考虑一个由N个异构智能体组成的网络,每一个智能体的动态方程描述为

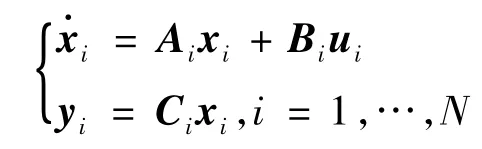
(1)

其中xi∈Rni,ui∈Rpi和yi∈Rq分别表示智能体的状态向量,控制输入和输出.Ai,Bi,和Ci是具有合适维度的矩阵并且满足以下几个标准假设.

假设1.(Ai,Bi),i=1,…,N是可镇定的.

假设2.(Ai,Ci),i=1,…,N是可检测的.

假设3.存在矩阵S∈RmXm满足σ(S)C+和矩阵R∈RqXm满足下列方程:

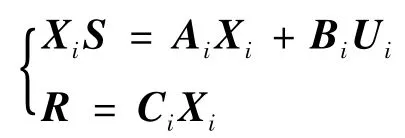
(2)

有唯一解(Xi,Ui),其中 Xi∈ RniXq,Ui∈ RpiXq.

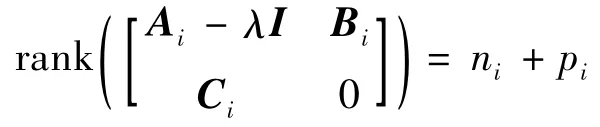
注2.本文中,矩阵S和R是自行构造的,在这里,我们取R=Iq.关于R的选取,文献[24]的附录C给出了说明,感兴趣的读者可以参考.

对于这个多智能体网络,我们用图G来 表示智能体间的信息交流拓扑,对于网络的拓扑结构我们作如下假设:

假设4.通讯拓扑图G无向且连通.

在实际工程应用中,智能体间的通讯是通过数字通讯网络中的不同通讯通道来进行的.这些通讯过程就不免会受到各种各样通讯限制的影响,如传输错误,通讯噪声等.在本文中,我们将各智能体间的通讯通道构建成一个受不确定性影响的传输系统,每个智能体的从邻居获取信息都是通过这个不确定通信通道[15].

3 异构多智能体网络的编队控制

我们针对每一个智能体提出了一个基于不确定通讯的补偿器,如下所示:

(3)

其中Δij表示智能体 i和 j之间的传输通道不确定性,vi∈Rq是补偿器的状态向量,c为耦合增益,hi是智能体的编队变量,满足Shi=0,i=1,…,N.对于此不确定性Δij,我们进一步假设其为范数有界:

假设5.对所有的 (i,j)∈ ε均存在 δij>0满足‖Δij‖ ≤ δij.

首先,我们设计补偿器(3)使得各补偿器的状态实现编队控制.

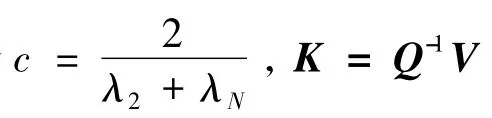
(4)

其中 Π =QΓ + ΓTQ+V+VT+(δm+ τ2)I,δm=分别表示网络对应的拉普拉斯矩阵 L的最小和最大特征值,则此时补偿器的内部状态能够达到编队控制.

此结果可依据作者的前期工作[4]和[15]得到.为完整起见,将其证明如下

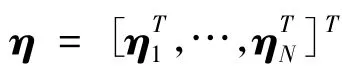
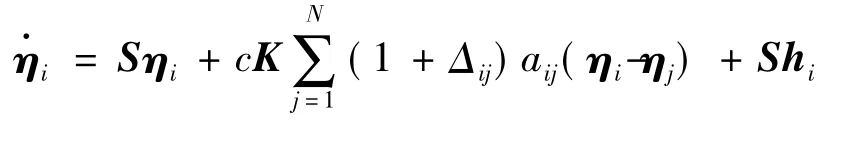
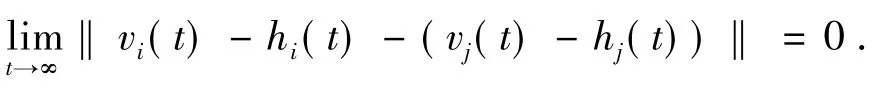
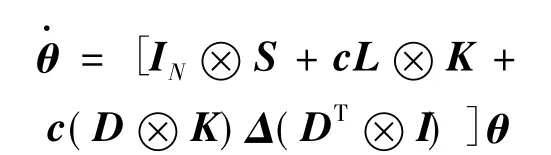
(5)

其中 θ =[θ1,…,θN]T.取 Lyapunov函数如下

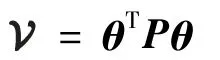
(6)

其中P∈RNnXNn是正定的,由此可得

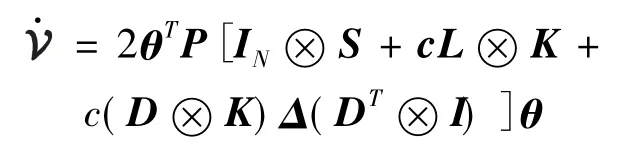
(7)

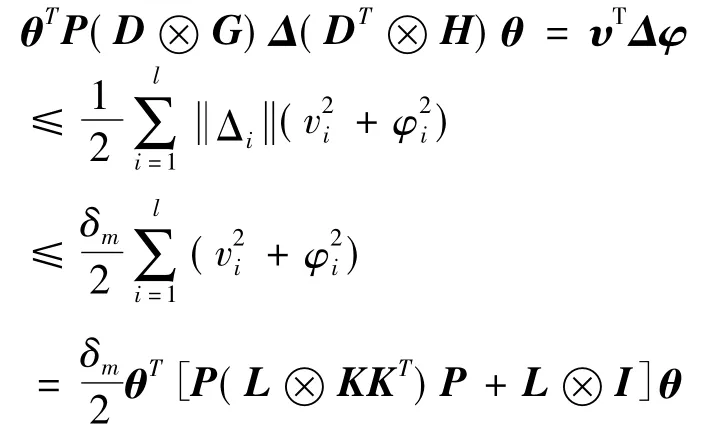
(8)

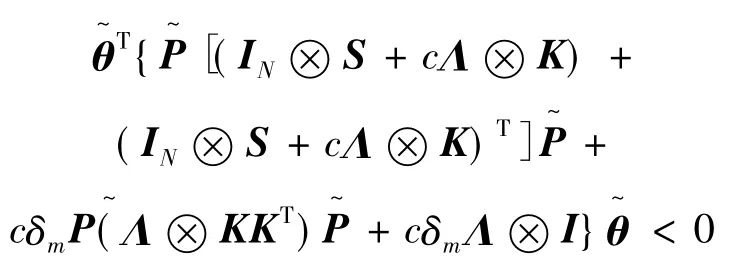
(9)

其中P选择为满足

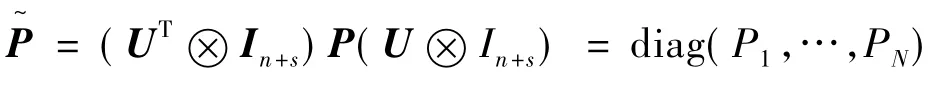
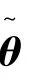
现代技术给体育带来了巨大变革，不仅改变了体育锻炼的形式，而且大力地推动了体育产业的发展。现代体育的社会背景是浮华的资本社会，人类因对荣誉与财富的追求，丢失了内心本性的追求与伦理道德的标杆。竞技体育追求的是“更高、更快、更强”，最初目的是让运动员不断突破个人的极限，挖掘人类最自然的力量，将人类恢复到最“强蛮”的状态，以抵御其他人和自然、天气的伤害。保障幸福与安然生存的前提条件是，公平公正地进行每一次肉体间的较量，公正和平、顽强拼搏的体育精神既是对人类思想道德的规约，也是对人类自我欲望的约束。

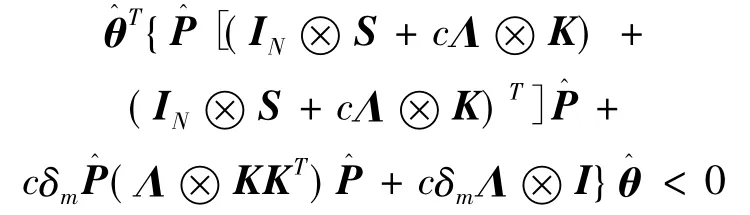
(10)

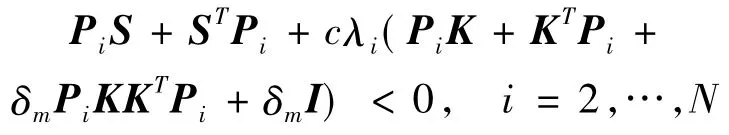
(11)

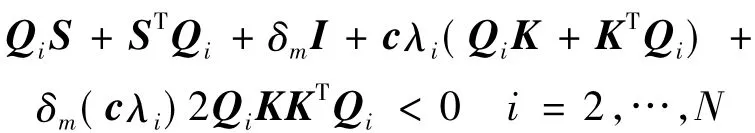
(12)

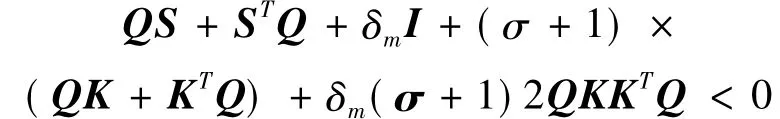
(13)

取QK=V并利用Schur补引理可得

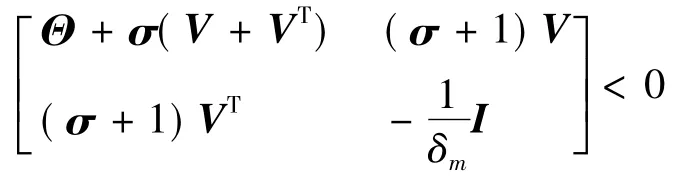
其中Θ =QS+STQ+δmI+V+VT.上式又可以改写为

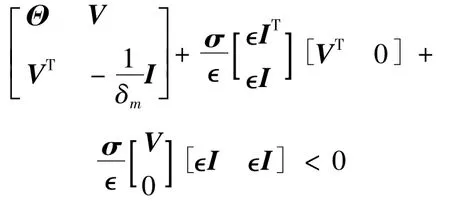
(14)

则式(14)成立,当

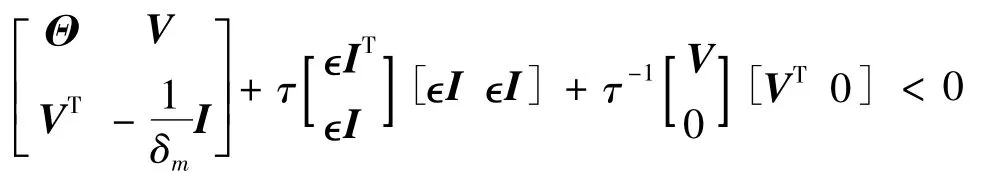
进一步利用Schur补引理,可以得出

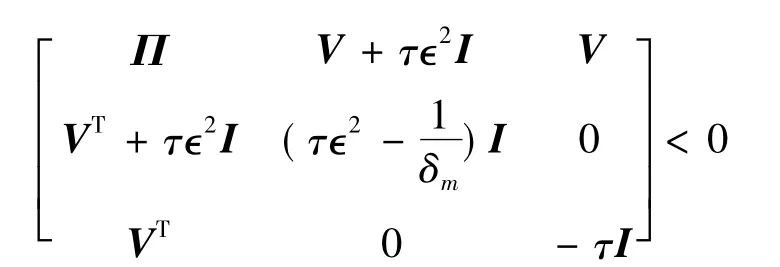
为了证明补偿器状态的编队实现,同样,我们可以写出误差项的网络化表达式

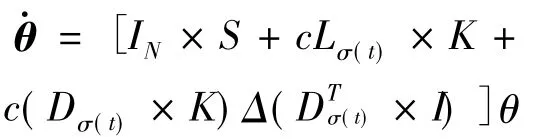
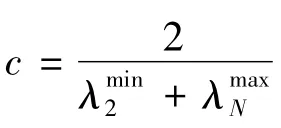
下面我们基于(3)的补偿器,给出一个基于输出信息的反馈控制协议:

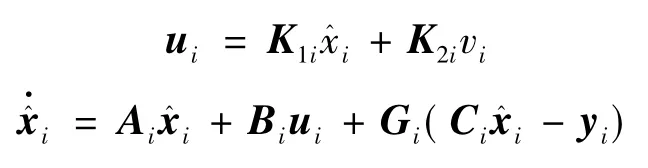
(15)

对于控制协议(13)中增益矩阵的设计,我们给出如下定理:

定理2.在假设1~3成立的条件下,取K1i和Gi分别满足 Ai+BiK1i和Ai+GiCi是Hurwitz的.K2i=Ui-K1i,其中(Xi,Ui)是调节方程(2)的唯一解.此时控制协议(13)能够实现异构网络(1)的编队控制.

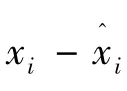
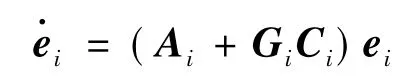
(16)

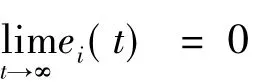
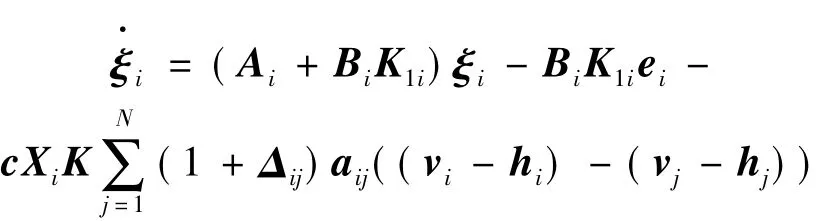
(17)

由 Ai+BiK1i是 Hurwitz的,以及

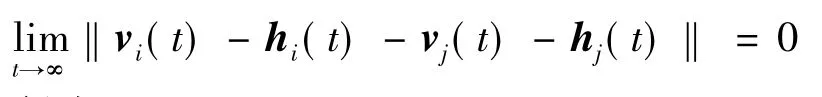
可以得出

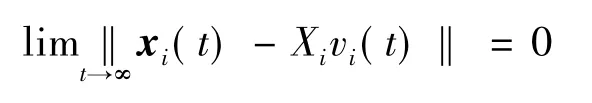
从而有

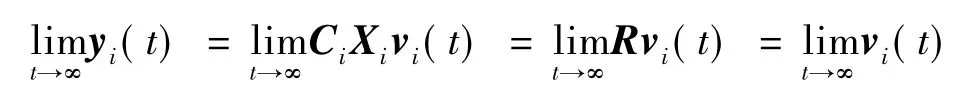
4 同构多智能体网络的编队控制

本小节,我们考虑一个由N个同构智能体组成的多智能体网络的编队控制问题,每个智能体的动力学特性如下:

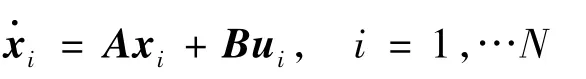
(18)

其中xi∈ Rn表示第 i个智能体的状态向量,ui∈Rp为系统输入,矩阵A和B为合适维度的常数矩阵.对于多智能体网络(16)的编队问题,在考虑通讯存在不确定性情况下,我们设计控制输入如下:

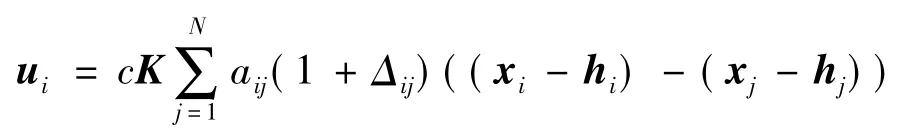
(19)

其中Δij表示智能体i和 j之间的传输通道不确定性,hi是智能体的编队变量,满足Ahi=0,i=1,…,N.同样我们假设Δij范数有界,满足假设5.对于输入的设计,我们有如下的定理:

定理3:在假设4和5成立的条件下,对于多智能体网络(16),设计,其中矩阵Q>0,V是下列线性矩阵不等式的一个解.

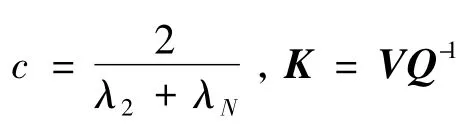
(20)

则同构多智能体网络(16)能实现编队控制.在(18)中,Θ=AQ+QAT+BV+VTBT+(δm+τ2)I,其余变量的定义与(4)相同.

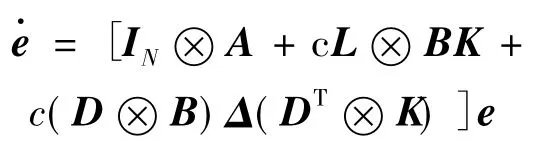
余下的证明过程与定理1的证明类同,为了简洁起见,证明过程在此省略.

注4.对于同构网络,与第3节不同的是,我们不需要设计补偿器,直接对输入设计状态反馈控制即可.这是因为各个智能体的动态特性是相同的,直接利用其状态信息就能够实现整个网络的编队控制.同样,这个结果也可以推广到切换图谱情形.

5 仿真验证

考虑一个由6个异构的智能体组成的网络,动态方程对应于(1)中表示为:

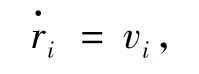
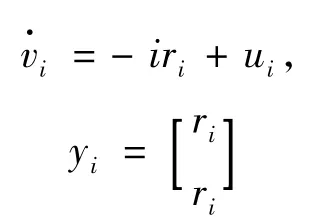
对应为

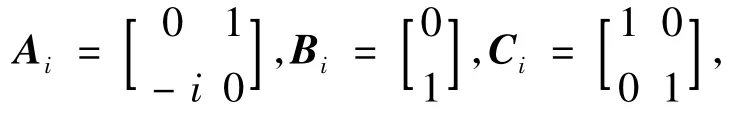
i=1,…,6,其中 ri∈R2,vi∈R2,yi∈R2,ui∈R2分别表示位置、速度、输出、以及控制输入.假设网络的拓扑结构在下面的G1和G2之间随机切换,每秒钟随机切换一次,这两个拓扑结构如下:

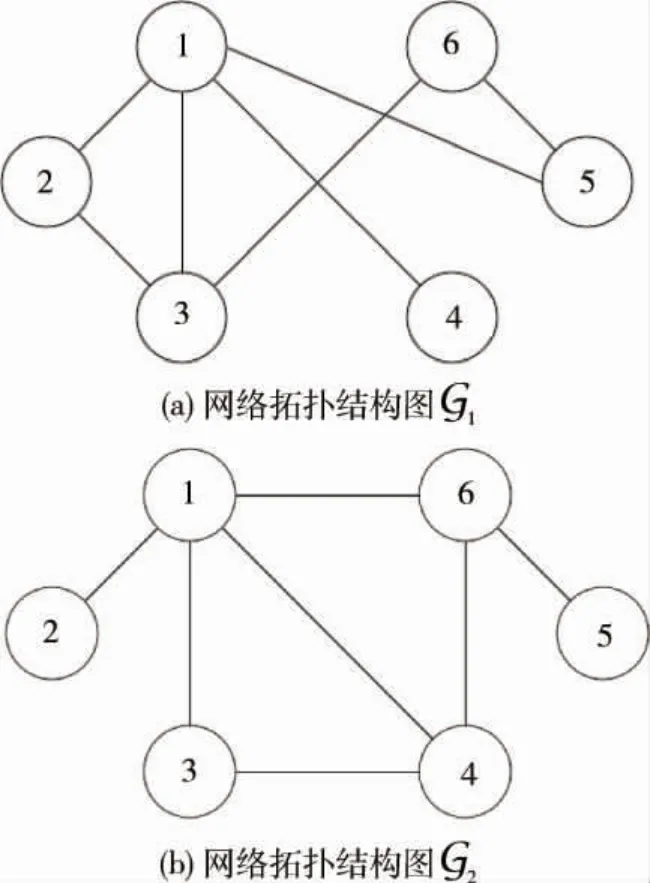
图1 网络拓扑结构图Fig.1 Communication topology

各个智能体之间的通讯存在满足假设5的不确定性,在拓扑图 G1中分别设计为 Δ12=0.2sint,Δ13=-0.3cost,Δ14=0.2cos2t,Δ15=-0.1sin2t,Δ23= 0.4cos3t,Δ36= 0.2sin3t,Δ45=- 0.6,Δ56=0.1sint.

在拓扑图 G2中,分别设计为 Δ12=0.2sint,Δ13=-0.3cost,Δ14=0.2cos2t,Δ34=-0.1sin2t,Δ16=0.4cos3t,Δ46=-0.6,Δ56=0.1sint.我们的控制目标是让6个智能体形成一个六边形的编队,取位置量分别为

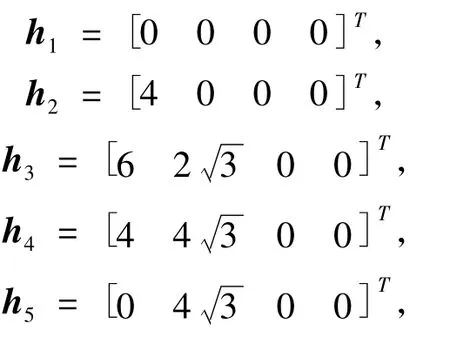
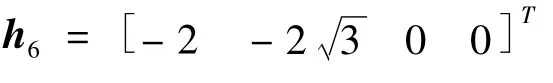
以及

依据定理2可求出调节方程(2)的解为Xi=I,Ui= [ i0 ].由此可以得出反馈增益矩阵K2i=Ui-K1i.如下

利用控制协议(3)、(13),各个智能体的位置轨迹曲线如图2所示,由图可以得出控制协议实现了目标的六边形编队.

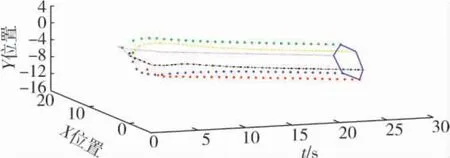
图2 各智能体的运动轨迹Fig.2 Trajectories of agents

6 结论

本文研究了不确定通讯网络下的多智能体系统的鲁棒编队控制问题.针对实际应用中,通讯通道出现的传输误差和噪声,我们将网络中的信道构建成一个统一的附加范数有界的不确定性的传递函数.我们首先对每个智能体分别设计了分布式的补偿器并得出了实现补偿器内部状态达到编队控制的充分条件.随后,对每个智能体给出了一个基于观测器的控制律以实现智能体跟踪到对应补偿器的状态,从而实现智能体网络的编队目标.作为异构多智能体网络的一个特例,我们也对同构多智能体网络的编队问题给出了控制律的设计方法.