基于核心素养的高中数学课堂之循循善“诱”
陈阳琴


[摘 要] 数学核心素养是具有数学基本特征的、适应个人终身发展和社会发展需要的人的关键能力与思维品质。基于数学核心素养的高中数学课堂教学,教师应将启发和诱导设计并实施教学的全过程中,帮助学生更好地掌握教材内容,促使学生积极思考,拓展思维。
[关键词] 高中数学;思维品质;探究
在《普通高中数学课程标准修订稿》中,明确提出六个数学素养:数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析。我们一线教师在备课和授课过程中,应善于启发和诱导,把“六个素养”渗透在教学的全过程,使学生在学的过程中能引起兴趣,认真听讲并积极思考,从而尽快更好地掌握教材内容,进而不断丰富和提高自己的知识,提升数学核心素养,并在教和学的过程中润物细无声地增强学生的行为习惯和品德修养。
那么,教师在教的过程中,如何使学生更快更好地掌握知识与技能,做到教而有方、启而得法、诱之有效、学而有得呢?笔者作为一线教师,结合自身的实践,不揣浅陋,谈谈自己的体会,以就教于同行,并与同行分享。
一、有效创设情境,激发兴趣
创设良好的情境,使课堂教学一开始就引人入胜,一下子就可以引燃学生的学习热情,刺激学生的兴趣点,让学生主动展开认知的探索,从而使课堂教学成功了一半。
案例1:在讲授《二项式定理》这节课时,可以先向学生介绍杨辉三角,即数字排列成一个大三角形,位于两腰上的数字均为1,其余数字则等于它上面两数字之和。这是宋代数学家杨辉在《详解九章算术》一书中记录下来的。在西方,直到1654年才有法国数学家巴斯加在论文中详细讨论了这个图形。我国比西方早了近400年。学生们都感受到了强烈的民族自豪感。那么,这个杨辉三角形与我们今天要学的二项式定理有何关联呢?这个问题马上引起学生强烈的兴趣,学生们非常主动地参与到问题的探究中来。接下来笔者顺理成章地让学生观察一次、二次、三次展开式,并让学生分别记录下各展开式中各个项的系数,那么,学生发现这些系数分别对应杨辉三角形中各行的数也就轻而易举。由此,让学生猜想n次展开式并证明就是水到渠成,一气呵成的了!
二、巧妙设置问题,启发思维
善于巧妙设置问题,启发学生思维,这不仅是数学教学中的技巧,也是使课堂教学能沿着课标要求逐步深入的重要环节。
案例2:在人教版必修一《方程的根与函数的零点》中,有这样的定理:若函数[y=fx]在区间[a,b]上的图像是连续不断的一条曲线,并且[fa?fb]<0,那么函数[y=fx]在区间[a,b]内有零点,即存在[c∈a,b],使[fc=0],这个[c]就是方程[fx=0]的根。这个定理对于学生来说比较抽象,为此,笔者在课堂上设置了几个问题让学生辨析,诱导学生进行深入思考。
片段
教师:若函数[y=fx]在区间[a,b]上满足[fa?fb]<0,则函数[fx]在区间[a,b]内一定有零点吗?
有的学生说:一定有;有的学生说:没有。
生1:(黑板上边画图边解说)请看函数[y=x]的图像,取区间[-1,1],满足[f-1?f1]<0,那么该函数在[-1,1]内有一个零点0,再看函数[y=1x]的图像,同样取区间[-1,1],满足[f-1?f1]<0,但我们发现该函数在区间[-1,1]内没有零点。
学生们频频点头,表示赞同。
教师:很好!那么我们来看下一个问题:若函数[y=fx]的图像在区间[a,b]上连续不断,且[fa?fb]>0,则[fx]在区间[a,b]内一定没有零点吗?
生2:没有零点,明显不满足定理的条件嘛!
部分同学马上做出响应“没错!”
教师:同学们都赞同这个观点吗?
生3:(自告奋勇站起来)可以有零点。比如函数[y=x2]在[-1,1]上图像连续,[f-1?f1]>0,但函数[fx]在[-1,1]内有一个零点0!
同学们爆发掌声为该同学点赞!
教师:非常好!那么剛才认为没有零点的同学是否也举个例子呢?
生4:只要将函数[y=x2]图像向上平移一个单位得到函数[y=x2+1],该函数在区间[-1,1]上图像连续,且[f-1?f1]>0,我们看到函数在[-1,1]内没有零点!
生5:我也有一个例子。比如[y=ex]在区间[-1,1]内无零点。
教师:同学们能够联系已学过的初等函数的图像作为例子学以致用,特别棒!
学生们深受鼓舞,学习热情更加高涨。笔者趁热打铁,又设置了以下问题:
教师:零点存在性定理中函数[fx]在区间[a,b]内零点是有且只有一个吗?
学生们满脸好奇,有的交头接耳交换看法,有的索性拿笔在草稿上认真演算起来。
生6:(激动地站起来说)老师,我想到了,“金蛇狂舞”!(同学们哈哈大笑)
这位同学在黑板上画出一个与x轴有多个交点的函数图像。
教师:好!很形象!以后我们在必修四会学习正弦函数[y=sinx]的图像就是这样的。(投影仪展示[y=sinx]的图像)
学生们深受启发,流露出求知的眼神。笔者抓住这个契机继续设问。
教师:请同学们思考,给定理增加什么条件时,函数在区间[a,b]上有且只有唯一一个零点呢?
学生们陷入了沉思,又是一番激烈的讨论。
生7:(兴奋地说)那就让函数图像不“跳舞”,就是只能上升或者下降呀!
教师:棒极了!用数学的语言又该如何表达呢?
学生们马上反应过来,异口同声地说出“函数具有单调性!”
教师:非常正确!确切地说是函数[fx]在区间[a,b]上具有单调性。
感悟:问题是数学的心脏。笔者不断通过基础性强、典型性高的设问唤醒学生的好奇心与探究意识,引导学生沿着教材内容积极思考探究,帮助学生更快更好地掌握数学知识的同时,提升自身的数学素养。
三、恰当变式延伸,诱导探究
变式延伸,不但是培养学生举一反三,灵活学习和掌握知识的关键环节,也是提高学生学习能力,增强学生具有深入钻研精神的有效途径。
案例3:高三总复习中三棱锥的外接球问题是近几年高考的一个热点,也是难点。学生由于空间想象力不足,解题时常常有一种“山穷水尽”的感觉。笔者从一道典型例题入手,变式延伸,诱导学生探究具有线面垂直关系的三棱锥的外接球问题。利用多媒体辅助教学,动态、直观呈现变换过程,从而促成学生更加深刻的理解。
片段
例:已知三棱锥[P-ABC]中,侧棱[PA,PB,PC]两两垂直,若[PA=2,PB=PC=1,]求三棱锥[P-ABC]的外接球的表面积。
教师:同学们,我们知道求三棱锥的外接球的表面积关键是确定什么?
学生:球心及半径!
教师:对啊!那么如何确定球心呢?
学生们瞬间懵了,开始了积极地思考。
笔者先用几何画板画出一个三棱锥及一个长方体,请同学们观察长方体相邻的三条棱的位置关系,学生们很容易发现它们两两垂直,进而启发学生发现该三棱锥可以是长方体的“一角”,学生们恍然大悟,那么将三棱锥补形成长方体就显而易见,这样三棱锥[P-ABC]的外接球与长方体的外接球是同一个,问题也就迎刃而解了。
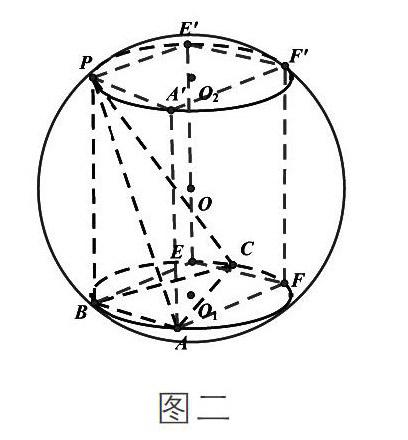
随后,为了与学生一起探究更一般的具有线面垂直关系的三棱锥的外接球问题,笔者设置了一道变式题:在三棱锥[P-ABC]中,[PB⊥面ABC,且PB=2,AB=3,∠ACB=π3],求此三棱锥外接球的体积。
有了例题的引导与铺垫,大部分同学第一时间想到了“补形”,可是怎么补形?学生们陷入了沉思。于是笔者让学生先进行组内探究,同学们交头接耳,各抒己见。在学生的合作探究学习中,笔者没有袖手旁观,而是承担协调、启发、引导的责任。经过一番激烈的探讨之后,学生们形成了两种不同的观点。一组学生说“补成直三棱柱”,另一组说“补成长方体试试吧”。最后笔者请他们各派一名代表陈述自己补形的具体做法。
根据学生的陈述,笔者利用几何画板与powerpoint动态呈现两种做法的补形过程。
教师:两位同学的精彩陈述特别棒!我们发现,两种方法最终都划归为线段[PB],[ΔABC]所在平面与球[O]相交所得的截面圆[O1]的半径及球的半径之间的数量关系,二 者有着异曲同工之妙。具有線面垂直关系的三棱锥的外接球问题可以通过补形法巧妙解决。
感悟:实践证明,数学课堂教学不能机械呆板,就题 论题,还应善于一题多解或者一题多变,引导学生不要满足已掌握的知识,而要不断深入思考,从而达到举一反三,主动学习的境界。同时,这也要求教师要有耐心和钻研精神,掌握多媒体技术,将信息技术与课堂教学深度融合,实现从教师的“教会”转变为学生的“学会”与“会学”,更加有效地提升数学课堂教学质量。
结束语:笔者所谈的体会,只是一个初步的探索和实践。不愤不启,不悱不发,教学中应使用各种教学手段,促使学生进行深入思考,拓展思维,从而提升其数学核心素养。教师在教学的过程中,只要有高度的责任心和对学生负责的精神,就会主动怀有探索和实践的意识,就会不断提高数学课堂教学质量,就会在数学课堂教学上不断创造出新境界。
[参 考 文 献]
[1]韩继芳.高中数学课堂情境创设中的问题和对策[J].数学教学通讯,2017(9).
[2]白露.例谈数学文化在中学数学教学中的渗透[J].数学教学通讯,2017(9).

