石英音叉陀螺多频率激励自启动算法

付 雷，孟 磊，冯立辉，崔建民，汤 一，要彦清

（1.北京理工大学 光电学院，北京 100081；2.北京晨晶电子有限公司，北京 100015）

石英陀螺以其体积小、可靠性高、成本低等优点，在军民领域具有广泛应用，目前向着数字化、集成化、高精度方向发展。Cao Hui-liang等人通过多种正交误差纠正方法将零偏稳定性降低至 3 (°)/h[1]。Georgia Tech早在2008年就提出了零偏稳定性为0.96 (°)/h的音叉陀螺[2]。Yang Cheng等人用同步积分解调器（SID）检测弱信号，配合自动增益控制与锁相环，零偏稳定性可达0.2 (°)/h[3]。Norouzpour-Shirazi A利用数字相位解调算法提取角速度信号，系统具有0.55 (°)/h的零偏稳定性[4]。Igor P.Prikhodko等人提出了实时温度自感偏置漂移补偿算法，将零偏稳定性从0.6(°)/h 降低到 0.2 (°)/h[5]。众多科研单位及企业如日本Epson公司、美国BEI公司已有商业化产品。美国SDI公司生产的SDD3000单轴精密数字陀螺仪，运行期间的零偏稳定性小于 1 (°)/h，在对温度、振动等环境稳定性和噪声要求苛刻的场合发挥出色。

数字化处理能提升音叉陀螺工作性能，本文从驱动频率定位精度与稳定性出发，在频率跟踪算法的基础上，提出多频率激励算法，当更换音叉或温度变化时，音叉能快速自启动，有利于提升陀螺稳定性与适配性。

1 频率跟踪算法

石英晶体由于压电效应作用，驱动叉指受驱动信号激励作恒频稳幅振动，敏感叉指产生微弱电荷信号，相关解调即可得到角速度大小。为了研制更高性能的石英陀螺，可利用数字电路对音叉进行驱动与检测以进一步提高精度。现有数字解调方法需采用稳频正弦信号作为驱动信号，调节频率控制因子控制信号频率。根据石英音叉陀螺的导纳圆可知其存在多个谐振频率点，串联谐振频率是最佳工作频率。由于音叉陀螺品质因数Q值很高，相当于带宽极窄的带通滤波器，由电路不稳定等因素导致的驱动信号频率偏移将导致音叉无法起振。温度变化时，音叉等效电学参数发生变化，会导致谐振频率改变，若驱动信号频率不能随之变化，同样会导致无法起振。

本文依据已有的“频率跟踪算法”[6]，通过检测产生的附加相移来动态调整驱动信号频率，使得驱动信号频率与石英音叉谐振频率的偏移最小，算法原理图如图1所示。

跟踪算法中的阈值参考量会随温度变化而改变，不同音叉间该值也不同，导致更换音叉或工作温度变化后音叉无法起振或获取稳定工作频率。本文提出一种基于粒子群的多频率激励方法，可实现不同音叉的频率自动匹配，实现更换音叉后无需更改驱动程序即可自启动，同样适用于温度变化后的音叉工作频率标定。

图1 频率跟踪算法示意图Fig.1 Scheme of frequency tracking algorithm

2 音叉陀螺自启动方法

频率跟踪算法需要阈值参考量才能对驱动信号进行频率调控，该参考量可由自启动方法提供。

串联谐振频率为石英音叉陀螺的最佳工作频率，此时驱动信号幅度较大，驱动叉指可获得较多能量，能够提升陀螺灵敏度，且频率变化产生的幅度抖动对该频率影响最小。当工作在串联谐振频率附近时，陀螺性能较好。

当驱动电路自激振荡时，石英音叉部分等效

电学模型与放大电路如图2所示[6]，其中C1为动态电容，L1为动态电感，C0为静态电容，R1为等效串联电阻。Cf与Rf为放大电路中的反馈电容与反馈电阻。

则石英晶体的等效导纳为：

图2 石英音叉等效电路与放大电路Fig.2 Equivalent circuit of quartz tuning fork and the amplifying circuit

驱动信号经过音叉与放大电路后放大倍数为：

对式(2)进行化简，

等式左右两边取平方并移项化简，可得：

进一步化简，并令等式左边为S，可得：

式(5)中C0、C1、R1、L1这4个音叉电学参数作为未知数，利用DSP内正弦波信号发生器生成谐振频率附近多个频率正弦信号去激励音叉，同时用AD采集不同频率下的驱动信号幅值，计算出放大倍数A,从而得到S。由4个方程求得 4个电学参数，再根据串联谐振频率可得到参考频率 f，计算频率跟踪算法中的阈值参考量，当更换音叉或温度变化时都能进行准确的频率跟踪，实现音叉起振。

当音叉未起振时，AD端采集信号多为噪声，方程不具有真实性，解得结果亦无效。故需要通过跳频进行预处理，使音叉大致工作在谐振频率附近，跳频法示意图如图3所示。通常石英陀螺的驱动频率在11 kHz到12 kHz范围内，间隔100 Hz对音叉进行10次激励，当音叉响应最大时，AD采集到的驱动信号幅度最大，对应频率最接近谐振频率。第二次跳频以第一次结果为中心频率，间隔10 Hz进行。持续进行多次跳频，使频率更加精确，直到最终频率范围锁定到 5Hz，此时可认为音叉已经起振，但不是最佳工作点，再进行数据采集与解方程运运算，并认为得到的结果符合精度要求。

图3 跳频法示意图Fig.3 Scheme of frequency scanning

实际应用中，音叉启动时间要求很短，而该算法运行时间较长，无法满足实际要求。可采用一次标定，二次启动的方法，针对一个新的音叉，先利用自启动程序进行标定，计算出所需阈值参考量，并储存在DSP芯片ROM中，进行二次启动时，直接从ROM中读取参考值，并完成音叉的频率跟踪与自启动。当需要对新音叉进行驱动时，程序会对音叉重新标定，并在ROM中存储新音叉的参数值，以便二次迅速自启动。通过这种二次启动的方式，提高了自启动算法的实用性。

3 跳频与粒子群算法

方程组求解的精度与速度影响了频率定位的精度与速度，所求方程为多元非线性方程组，无法求出解析解，只能通过迭代法求出满足一定精度的数值解。常见求解方法有二分法、弦截法等，这些方法都不需要求解导数值，计算效率更高，但收敛速度慢；牛顿迭代法作为最基本最核心的方法，至少二次收敛到单根，收敛速度有保证，但其关键问题是收敛性受初值影响大，初值选取不当将效率低下，甚至发散，无法得到解。

本文采用基于跳频法预处理的粒子群算法对方程组进行求解，迭代800次左右，上位机运行只需0.5 s即可得到所需解，求解精度可达10-20。

粒子群算法（Particle Swarm Optimization, PSO）是Kennedy和Ebe通过模拟鸟群觅食过程中的迁徙和群聚行为而提出的一种基于群体智能的全局随机搜索算法。PSO算法容易理解，参数少易于调整，对非线性、多峰问题具有较强的全局搜索能力，并且不受初值影响[7-8]。

在粒子群算法中，最优值问题的潜在解是搜索空间中的一只鸟，称之为粒子，由优化函数可计算每个粒子的适应度值（Fitness Value），每个粒子都有自己的速度决定下次前进的方向和距离，所有粒子追随着当前最优粒子在解空间中不断探索，直到全部收敛于最优解。

粒子群初始化为一群随机粒子，计算他们的适应度值，通过迭代来更新并记录最优解。在每一次迭代中，粒子通过两个值来更新自身，一是粒子本身的最优值，称为个体极值，二是整个种群中的最优值，称为全局极值。

粒子群算法的速度更新公式如式(6)所示[9-10]：

从一次速度更新后，相应的粒子位置也要做更新，如式(7)所示：

方程求解问题可等效为寻找函数零点问题，同时满足四个函数值最接近0的解即为期望解。将适应度函数定义为四个函数值绝对值之和，故解方程问题转化为求适应度函数的最小值，依据适应度值确定粒子群的个体最优与群体最优，确定所有粒子最优值与群体最优值后，进行速度与位置更新，更新完毕后，用新的粒子进行下一次迭代，直到适应度满足要求，达到4×10-20。此时得到的解满足精度要求，可用其计算谐振频率，并得到频率跟踪算法中的阈值参考量。

4 实验结果

为探究该自启动算法在实际应用中的可行性，对跳频法和跳频法与粒子群法两种方法在 DSP平台下进行实验，硬件开发原理示意图与硬件开发平台图如图4～5所示。

图4 硬件开发原理示意图Fig.4 Schematic diagram of hardware development

图5 硬件开发平台图Fig.5 Hardware development platform

对于同一驱动电路，未加入自启动算法时，更换音叉后，音叉无法起振，系统工作异常。当加入自启动算法后，音叉能正常起振，验证了多频率激励算法的可行性。由于谐振频率处，经AD采集得到的驱动信号幅值接近最大值，可用该值判断频率是否为谐振频率，即反映了频率定位精确度。

对两个音叉通过两种方法进行一次标定与二次启动，记录启动时间、谐振频率值与AD采集值的标准偏差，实验结果如表1、表2所示。将AD采集值作图，结果如图6所示。

图6 AD采集值结合法与跳频法结果对比Fig.6 Comparison between two methods of the acquisition value of AD

由表1与表2数据可得，使用粒子群与跳频结合方法得到的AD采集值标准偏差小，说明驱动端幅度稳定性较强，音叉工作状态良好，故粒子群与多频率激励结合的方法在音叉自启动中可行。

对比同一音叉的两种启动方式可知，使用粒子群与跳频结合方法启动时间比跳频法短3 s左右，AD采集值比跳频法大，说明频率定位更精确，标准偏差也更小，比跳频法结果稳定性提高了一倍左右。

表中时间为一次标定启动时间，该时间与硬件性能相关。当进行一次标定确定参考值后，二次启动可1.5 s内完成，与实际应用中的需求相符。

表1 音叉一两种方法启动结果Tab.1 Results of the first gyroscope by the two methods

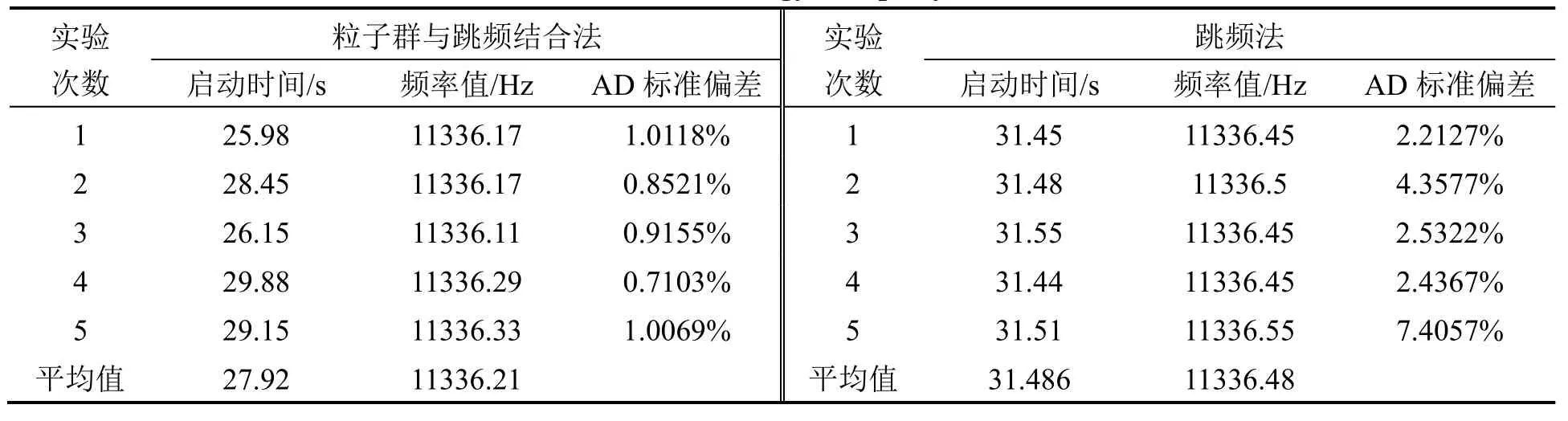
表2 音叉二两种方法启动结果Tab.2 Results of the second gyroscope by the two methods

5 总结展望

石英音叉陀螺驱动信号的频率稳定性对系统性能有很大影响，在频率跟踪算法的基础上，通过粒子群算法与多频率激励结合方法，实现了音叉更换时系统自动进入工作状态。实验探究了跳频法和跳频与粒子群结合两种方法，表明两种方法都可以用于石英音叉陀螺的自启动，但跳频与粒子群结合法启动速度比跳频启动更快，频率定位更精确，驱动端工作更稳定，有利于提高系统适配性与工作效率。