基于惯性测量单元的运动员呼吸状态监测方法

杨 海，罗 涛，李 莉，梁海波，张 禾

（西南石油大学 机电工程学院，成都 610500）

运动员在训练过程中需要对其身体机能进行各方面的监测防止过度训练，过度训练会造成身体的损害和情绪的低落。因此需要对其肺活量、最大吸氧量、心率、呼吸频率、尿液以及体内血红蛋白、血乳酸、二氧化碳浓度等生理生化方面进行反馈监测[1]。其中呼吸频率是最重要的监测方内容之一，运动员可以通过训练控制呼吸频率达到最佳的训练状态，呼吸与脉搏之比为1∶4，监测运动员呼吸频率可以推算出心率，体内细胞乳酸以及二氧化碳含量，且相对其他生理生化信息的监测，呼吸的监测要更加方便简洁[2]。

目前呼吸监测的方法有很多如：呼吸道传感器直接监测法[3]，基于呼吸音的呼吸监测方法[4]，肌电信息分析法[5]等。其中呼吸道传感器直接监测法需要将测量装置直接安置在呼吸道上，给受试者造成不适，且对正常呼吸节奏的影响会带入测量结果，进而形成误差。由于基于呼吸音的呼吸监测方法目前无法实现呼、吸周期的识别，只能对呼吸气流速度的绝对值进行模拟，从而降低了呼吸监测的可靠性。通过对肌电信号的分析获取呼吸波形的方法需要得到心电图，但是无法进行实时跟踪，不适用于在运动状态下进行测量。

惯性测量单元（Inertial Measurement Unit, IMU）是测量物体姿态角以及加速度的装置，一个IMU包含了三个单轴的加速度计和三个单轴的陀螺仪，加速度计实时测量物体在载体坐标下的三轴加速度信号，而陀螺实时测量载体相对于导航坐标系的角速度信号，并以此利用算法得出物体的姿态。IMU体积小、质量轻、功耗小、成本低、可靠性高等优点，在民用和军用定位领域都呈现出广阔的应用前景[6-9]。由于 IMU各方面优点，因此已有国内外学者将其应用在人体，对人体各项数据进行测量[10-13]，如朱庄生提出的利用IMU实现对人体步数的监测，王雪梅通过IMU测量人体手臂运动信息，Prabancoro Adhi Catur Widagdo利用IMU对肢体运动的追踪等[14]。

然而这些都是运动幅度较大，造成测量数据的变化范围也较大，此外由于惯性测量单元量测噪声的影响，使得最终呼吸状态的测量精度会由于被测对象的运动产生干扰。因此针对IMU的误差分析以及补偿方法的研究也从未停止[15]。

综上所述，针对呼吸信号微弱以及单个IMU无法消除人体运动时噪声的缺点，本文提出一种基于卡尔曼滤波算法的差分双惯性测量单元呼吸监测方法，采用双IMU分别固定安装在待测运动员的前胸和后背，进而测得其呼吸时前胸和后背角速度和加速度。由于胸腔活动导致的相对运动，通过对IMU测量的加速度和角速度参数进行差分解算和卡尔曼滤波，得到运动员实际的呼吸运动采样曲线，实现运动员在动态环境下的呼吸频率和呼吸深度实时监测。

1 呼吸监测动态差分解算模型

人体的胸廓会随呼吸而起伏，当人体处于不同的状态时，胸廓的起伏幅度也有所不同，且在呼吸时胸廓是前后运动跟上下运动的叠加。根据惯性理论可知，惯性测量单元包含三轴的加速度计和三轴的陀螺仪，加速度计检测物体在载体坐标系下的三轴加速度信号，而陀螺仪检测载体的角速度信号，进而实现物体在三维空间中角速度和加速度的测量，因此根据呼吸改变载体坐标系下加速度参数为依据，设计出人体的呼吸运动检测模型。

1.1 人体呼吸运动采样模型

在呼吸频率测定时采用惯性测量单元，基本思路是前后两个IMU采集到的数据进行差分，解算出呼吸时胸廓扩张与收缩的加速度，通过加速度的幅值与周期判定呼吸深度与呼吸频率。运动载体在理想静止状态下惯性元件所测量3个坐标轴方向的加速度矢量和等于重力加速度，并且其所测量的三轴角速度为地球自转角速度，约为7.27×10-5rad/s，其数量级远小于运动载体在移动过程中的角速度，因此可以认为运动载体在静止状态下其三轴角速度均趋近于 0。因此，根据这一特性可以将惯性测量单元固定在胸部来测定呼吸时胸廓不同方向的加速度。一个IMU只能测定前胸各方向的加速度，但人体在呼吸时后背也会跟随前胸有轻微的起伏，且在走动或运动时所产生的幅度相比于胸廓的起伏要大得多，因此需在前胸与后背各固定一个IMU，通过求取两者差分相对运动的形式来消除运动产生的绝对速度对实验结果的影响。图 1(a)所示是在人体在穿有佩戴IMU的示意图，图1(b)是人体在呼吸时胸廓变化示意图。IMU的三轴加速度计实时测量人体呼吸时胸廓的加速度信号，三轴陀螺仪实时输出产生的姿态角速度信息，在实时获取了胸廓的加速度信息和姿态信息后对呼吸进行实时解算。

图1(a) 人体穿有佩戴IMU示意图Fig.1(a) Human body worn with IMU

图1(b) 人体呼气吸气胸廓变化示意图Fig.1(b) Human chest changes during inhalation and exhalation

1.2 呼吸运动IMU姿态解算

在IMU位置姿态更新算法中，比较经典的是利用四元数理论建立人体的姿态四元数模型，并通过该模型对系统的位置、姿态进行更新解算[16-18]。

人体与IMU固联的坐标系为载体坐标系（b系），取地理坐标系（g系）为导航坐标系（n系），并规定 xn、yn、zn的指向依次为东、北、天。设人体的航向角为ψ，俯仰角为θ，横滚角为γ。利用人体的姿态角可以得到人体的姿态变换矩阵，另安装在人体上的惯性元件（陀螺仪和加速度计）的输出是以地心惯性坐标系（i系）为参考基准的，且与地球固连的为地球坐标系（e系）。定义导航坐标系（n系） 到载体坐标系（b系） 之间的转换采用三次单轴旋转的方式来实现，且旋转顺序表示为：

IMU数字算法以递推迭代的形式表示，即采用系统微分方程组描述形式，将人体过去前一时刻的信息和最近时刻的惯性器件的采样值作为输入，通过对微分方程逐次递推计算出当前时刻的信息。

人体姿态更新的四元数微分方程为：

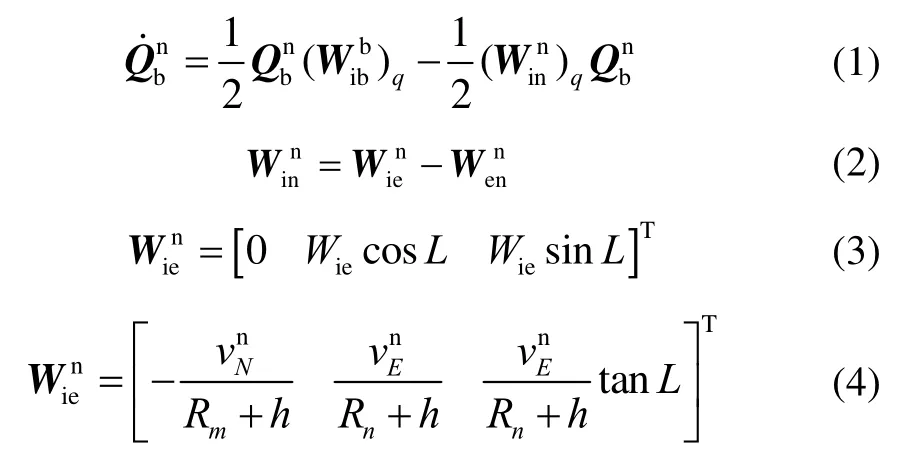
前后两个 IMU分别测出前胸与后背的三轴加速度和三轴角速度，在得到角速度后还需通过姿态转换矩阵将其转换为欧拉角。因为前胸与后背两个IMU所测量出呼吸时胸廓的三轴加速度信息并不在对应轴向的平面内，通过姿态转换矩阵可以将前后所测出的加速度转换到同一导航坐标系内然后再进行相应的差分运算。

姿态转换矩阵的方程为：

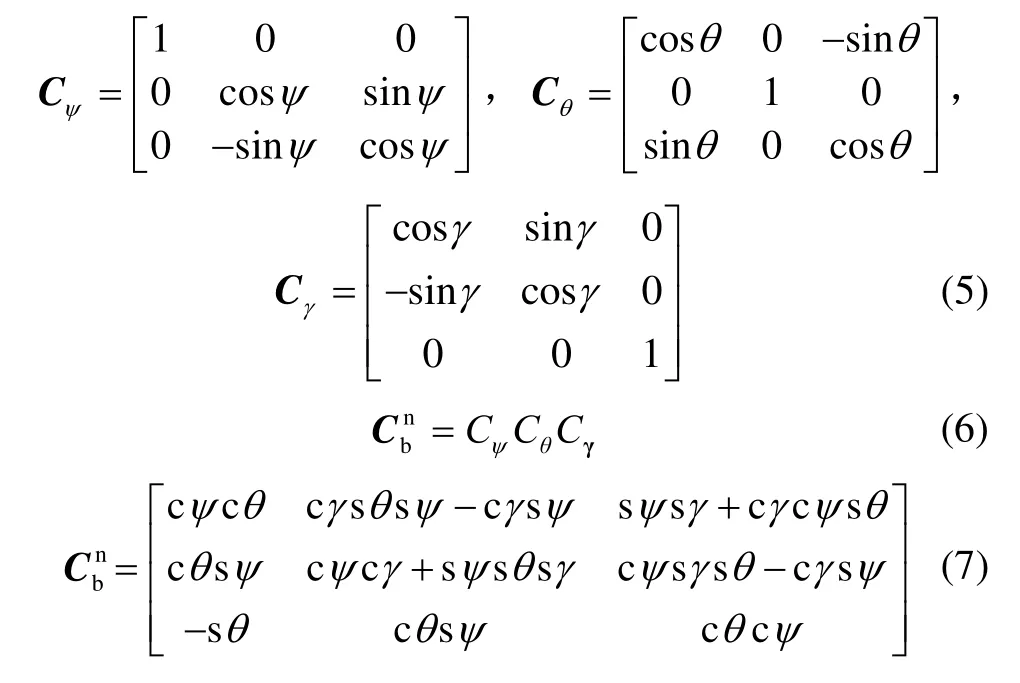
式(6)中字母“c”代表余弦函数“cos”，字母“s”代表正弦函数“sin”。通过设定呼吸加速度监测模型中的状态向量为并同时解算即可得到人体呼吸运动加速度的状态方程，其方程如下：

其中，uk表示状态噪声矩阵。

在得到状态方程后，通过解算即可得到呼吸加速度的观测方程，观测方程如下：

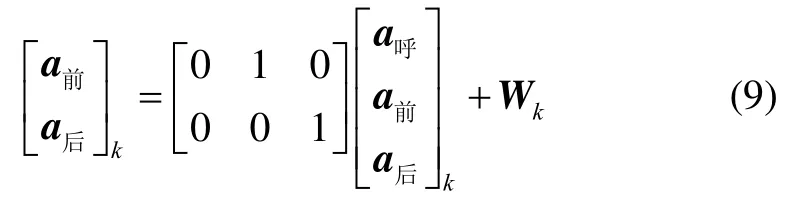
其中，Wk表示观测噪声矩阵。因此可以得到呼吸监测加速度的空间状态方程为：

其中，Fk+1,k表示异步状态传递矩阵，Hk表示量测矩阵。

利用差分方法得到呼吸的加速度状态方程后，为了提高监测系统的稳定性，需要对状态空间方程进行滤波处理，很容易发现，状态空间方程是一个线性系统。卡尔曼滤波（Kalman Filter, KF）是线性系统中最常用的滤波方法之一，KF方程构成包括两组方程，分别为时间更新方程和测量更新方程。

时间更新方程总结如下：

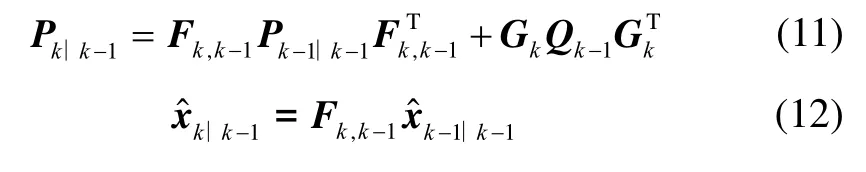
其中，Qk-1是协方差矩阵的过程噪声，Pk∣k-1是一个后验误差协方差矩阵。

测量更新方程为：

其中，Kk为卡尔曼滤波增益，Pk为观测噪声W的协方差，假设为高斯白噪声其均值为零。

因此，整个模型计算过程如图2所示。

图2 模型计算流程图Fig.2 Experimental flow chart

2 实验验证

2.1 实验平台搭建

本实验选取JY901型IMU作为呼吸运动监测传感器，其集成高精度MEMS三轴陀螺仪和三轴加速度计，可以进行四元数计算，采用高性能微处理器和先进的动力学解算与卡尔曼动态滤波算法，能够快速求解出物体当前的实时运动姿态。且体积小、数据传输方便、动态稳定性高等优点，静态精度为 0.1°，动态精度达到0.05°，由于在实验过程中人体呼吸幅度对比于其他运动幅度相对较小，所以实验设备的精度和稳定性是设备选型中最重要因素之一。该型 IMU质量轻，仅为13g，其数据传输方式通过无线蓝牙进行传输，并通过串口将数据实时传输至上位机中。JY901型IMU最高数据输出速率为200 Hz，并且价格低廉，应用广泛，非常适合于本系统所搭建的低成本IMU呼吸运动检测实验平台，其实验如图3所示。

图3 实验设备Fig.3 Experimental equipment

在本次验证实验中考虑到呼吸运动的低频特性以及为了提高数据处理速度和降低数据处理量，同时提升监测系统的实时性，设定JY901型IMU的输出信号采样频率为10 Hz，采样点数为2 000，验证主要分为三个步骤来进行，分别测量人体在静坐、正常行走和正常跑动时的呼吸胸廓变化时的加速度参数，从而实现对本文所提模型进行逐步实验验证。

2.2 实验数据采集分析

第一步对静坐时呼吸运动参数监测，其分别安装在实验人员前胸和后背的 IMU测量得到的加速度信息如图4所示。将IMU测量的呼吸运动加速度信息和角速度带入差分卡尔曼滤波呼吸运动监测模型中，得到静坐时的呼吸运动加速度曲线，如图5所示。

图4 静坐呼吸前胸后背加速度Fig.4 Respiratory acceleration of front chest and back during sitting quietly

从图5中可以看出人体在静坐时呼吸较平缓且稳定，在一定的范围内上下波动。通过对呼吸加速度曲线进行幅值和频率的计算可以得出，实验人员静坐时的呼吸加速度幅值为0.24 m/s²，呼吸频率为17 Hz，呼吸深度的方差为0.018 (m/s2)2。

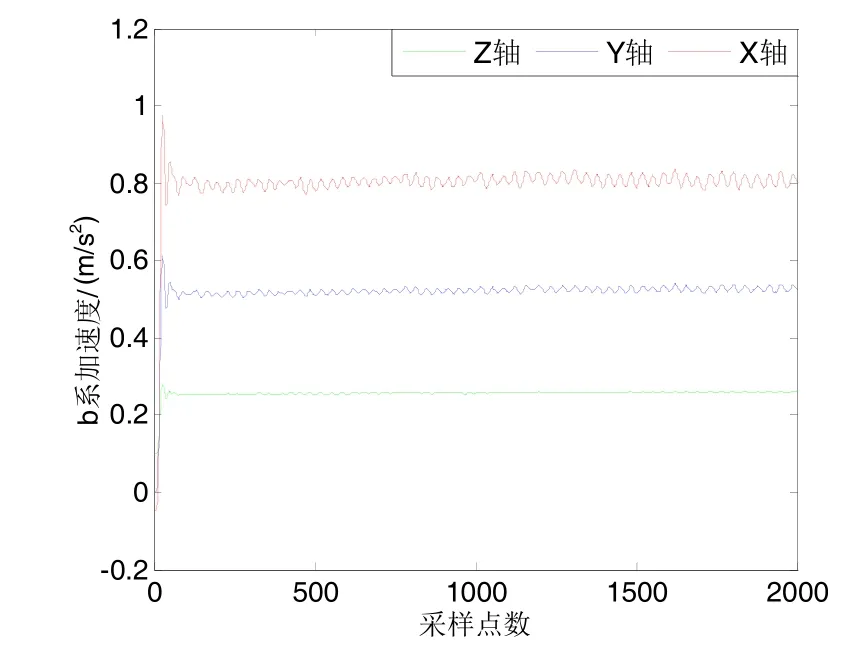
图5 静坐呼吸加速度Fig.5 Respiratory acceleration during sitting quietly

第二步测量人体正常走动时的呼吸加速度。其实验过程中测量得到的实验人员呼吸过程的加速度曲线如图6所示，并且经过差分卡尔曼滤波解算后的纯呼吸加速度曲线，如图7所示。

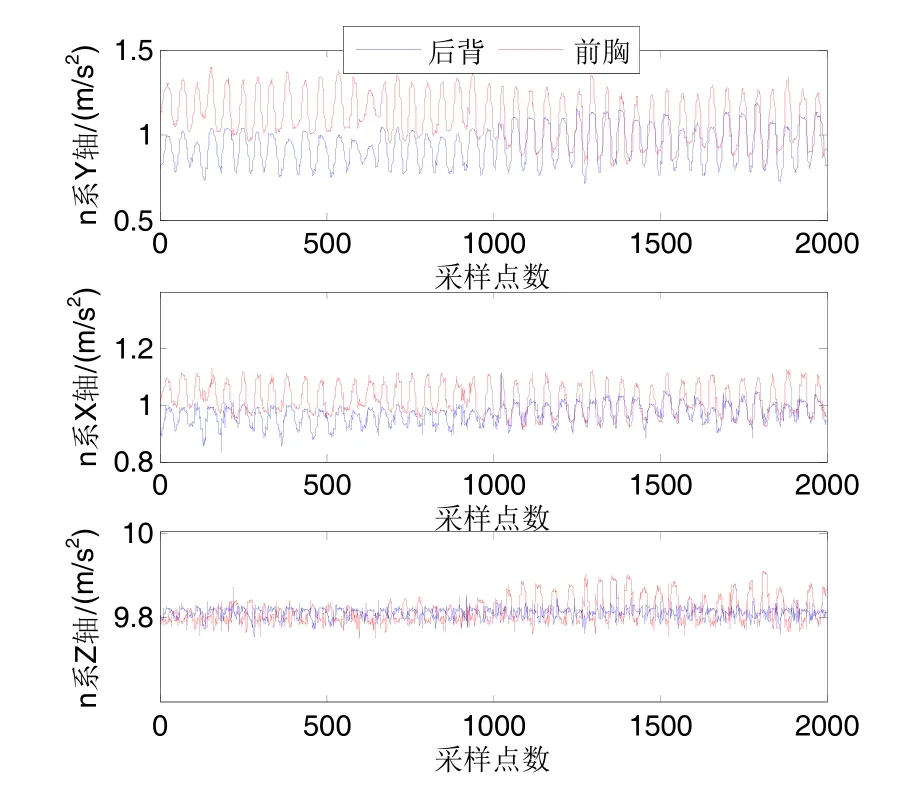
图6 正常走动呼吸前胸后背加速度Fig.6 Respiratory acceleration of front chest and back during normal moving

图7 正常走动呼吸加速度Fig.7 Respiratory acceleration during normal walking

在图7可以从定性的角度看出正常行走时人体的呼吸相对于静坐深度有明显增大，通过算法得出人体在此种状态下的呼吸深度为0.38 m/s²，频率较静坐时有所降低为15 Hz，呼吸深度的方差为0.022 (m/s2)2。

第三步则探讨在人体正常跑动时的呼吸运动测量情况，实验平台测量得到的实验人员前胸和后背的加速度曲线如图8所示。同时将所测量的数据带入到本文提出的差分卡尔曼滤波呼吸运动监测模型中，得到解算后的纯呼吸加速度曲线如图9所示。

从图9中可以清晰看出，人体跑动时的呼吸明显变得急促频率也有显著提高而深度却降低了。同时在图9中还可以看出实验数据产生了漂移，其主要原因是由于人体在跑动过程中各个方向的运动幅度较大，通过四元数解算后的姿态矩阵出现了一定的漂移，另一方面是因为身体大幅度的运动导致了固定在身体上的IMU安装位置出现了一定的移动。通过对解算后的纯呼吸加速度进行频谱分析后，得到实验人员在正常跑动后的呼吸深度为0.19 m/s²和呼吸频率为25 Hz。由于图9中曲线漂移现象较明显，所以计算出此种状态下呼吸深度的方差为0.028 (m/s2)2。

图8 匀速跑动呼吸前胸后背加速度Fig.8 Respiratory acceleration of front chest and back during running at constant speed

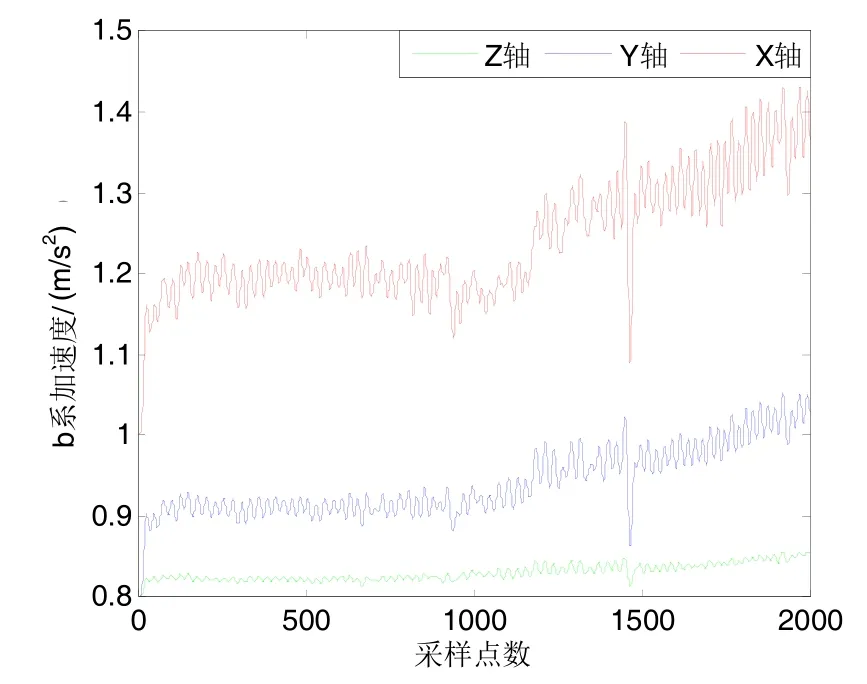
图9 匀速跑动呼吸加速度Fig.9 Respiratory acceleration during constant running

本实验采用差分的卡尔曼滤波模型和算法分别得到实验人员静坐、正常走动以及正常跑动情况下呼吸呼吸频率和呼吸深度，人体呼吸信号相对于运动信号十分微弱，该差分模型有效隔离了运动加速度和角速度的影响，如果不采用差分，仅对实验数据进行卡尔曼滤波，此种情况下只能反映运动步态信息，呼吸信号将被淹没。结合实验者佩戴呼吸面罩测量的呼吸频率，得到分析结果如表1所示。

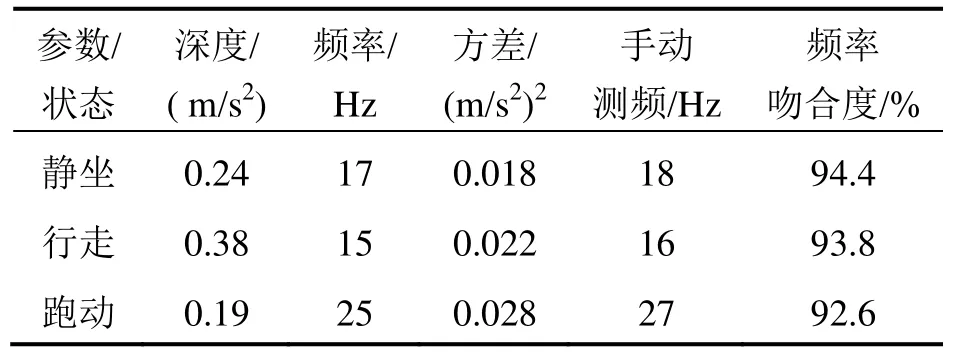
表1 呼吸参数对照表Tab.1 Comparison on respiratory parameters

由表1可以看出，采用本文提出的双IMU差分卡尔曼滤波呼吸运动监测模型能够对人体静坐、行走以及跑动情况下的呼吸频率和呼吸深度进行有效的监测，其中呼吸频率的监测精度均保持在90%以上，且对呼吸深度的监测方差也较小，因此该系统能够实现人体在动态环境下的稳定准确的呼吸状态监测，能够很好地用于老人健康监测以及运动员的体能评测等。

3 总 结

针对本文提出的基于卡尔曼滤波算法的差分双惯性测量单元呼吸监测方法，通过选用JY901型IMU进行多次实验验证，结果论证了IMU在频率10 Hz测量人体呼吸的可行性，且测量出了人体在不同姿态下的呼吸加速度，通过模型和算法解算得到人体静坐时呼吸频率为17 Hz，匀速跑动时呼吸频率为15 Hz，正常走动时呼吸频率为 25 Hz，通过将此种呼吸监测方法对比呼吸面罩法得出该方法具有较高的测量准确度，达到在90%以上。该方法较传统的呼吸监测方法有明显的优势，扩展了IMU的应用领域，由于IMU的各项优点，将其做成高品质的可穿戴式设备，广泛应用于运动员的训练与比赛当中，在训练中用此方法测定呼吸频率省去了各种昂贵笨重的设备，且可以进行实时解算出运动员心率状况以防止过度训练而造成身体机能的损伤。但是由于IMU自身存在一定的缺陷，在实验中会造成了漂移现象，在后续实验中还需进行研究和改善。