速率偏频激光陀螺惯导系统航向敏感误差分析与补偿
江一夫,李四海,徐兵华,严恭敏
(1.西北工业大学 自动化学院,西安 710029;2.西安航天精密机电研究所,西安 710100)
与机抖偏频一样,速率偏频技术是解决激光陀螺锁区问题的另外一种方式。速率偏频要求激光陀螺敏感到持续的旋转角速度,因此可以与旋转调制技术复合利用同一转位机构,既可以避免机抖偏频频繁过死区产生的额外随机游走误差又实现了随机常值零偏的自补偿[1-3],既可以发掘出激光陀螺的极限性能又没有额外增加硬件成本,是实现高精度自对准的绝佳途径。
惯性导航领域中将方位相关的寻北误差,归结为航向敏感误差(Heading-Sensitive Error, HSE)。航向敏感误差主要与多位置系统参数不一致,磁场、温度场不均匀等因素有关,在平台惯导系统中一般采用最小二乘模型参数拟合和分段插值补偿的方法[4]。文献[5]针对双位置对准中航向敏感误差建立了理论模型,认为其航向敏感误差主要由第一位置的水平姿态对准误差引起。文献[6]采用基于试验数据建模的方式,通过在多个方位和水平倾角下进行大量的寻北测试,基于寻北结果建立航向敏感误差与水平姿态角和方位角的关系,并对系统后续的寻北结果进行补偿,提高捷联式寻北仪的寻北精度。这种方法操作复杂、耗时长,仅由试验测试数据直接辨识航向敏感误差参数,不区分航向敏感误差的影响因素,存在测试平台复杂和辨识模型适用性的问题。文献[7][8]主要研究了恒速偏频惯导系统,其中文献[8]分析了标定安装矩阵误差对寻北精度的影响,提出了将安装矩阵参数误差对航向敏感误差的作用视为一个整体进行标定的方法,文献[8]理论分析认为,惯组在 0.057°的水平倾角下,2″安装矩阵误差会引起30″的航向敏感误差。由于捷联惯导系统的倾角能够达到 5°以上且安装矩阵参数随机变化量很容易超出 2″,因此恒速偏频方案的航向敏感误差在大倾角下难以准确补偿,不再适用于高精度寻北系统。
本文主要针对正反连续旋转速率偏频方案,从速率偏频系统的数学模型和卡尔曼滤波对准误差公式出发,分析可能产生航向敏感误差的各误差源,重新明确引起速率偏频系统倾斜状态航向敏感误差的主要因素,并提出一种简单有效的补偿措施,最终试验验证其可行性,提高了系统的倾斜全方位寻北精度。
1 速率偏频系统模型的及坐标系定义
为了能够基于一个旋转台,使三轴陀螺都能敏感到旋转角速率,从而实现速率偏频,系统中激光陀螺采用如图1所示的倾斜安装方式[9]。

图1 速率偏频激光陀螺惯导系统安装方式Fig.1 Installation of rate-bias laser-gyro inertial navigation system
定义g系为三轴陀螺敏感轴构成的非正交系,定义g0系()为陀螺正交参考坐标系,xg0轴与陀螺敏感轴xg重合,yg0轴在 xgyg平面内,zg0与 xg0、构成正交系,实际中非正交系g与g0系之间存在小角度安装误差。定义p系为转位机构的台面坐标系,与转位机构的旋转轴重合,xp与xgo在转台台面上的投影重合,yp与 zp、 xp构成正交系。
若陀螺不存在安装偏差角,则图中αxx、αyx、αzx三者的理想值为 54.7356°,理想的斜转直矩阵可以表示为

设转位机构在电气零位时的p系为捷联惯导载体坐标系b系,寻北过程转位机构绕 zp中的旋转角速率为ω,则:

进一步,设当地东北天地理坐标系为n系,θ、γ、ψ分别为捷联惯导系相对地理系的俯仰、横滚和航向角。寻北过程中水平姿态角都为小角度,因此方向余弦矩阵可以简化为

2 对准误差公式
根据捷联惯导误差方程,对准误差可以表示为[10]:

式中,φU、φE、φN分别表示航向对准误差、俯仰对准误差和横滚对准误差,、、分别表示北向速度误差二阶导数、东向速度误差一阶导数和北向速度误差一阶导数,▽1N为等效北向加计零偏变化率,▽E和▽N分别表示等效东向加计零偏和北向加计零偏,εE为等效东向陀螺零偏,g为重力加速度,ωie为地球自转角速率,L为当地地理纬度。静基座条件或振动条件下(平均有效速度为零)对准以速度误差作为观测值,速度误差的各阶导数、、是准确已知的,其引起的对准误差可以等效为零。式(4)因此可以简化为

可以看出影响寻北精度的误差源主要包括等效东向陀螺零偏、等效东向加计零偏和等效北向加计零偏随时间的变化率。其中等效北向加计零偏变化率属于无法补偿的随机误差,此处暂不考虑其影响,而等效东向陀螺零偏是最主要的误差源,主要由三方面因素构成,包括逐次启动常值零偏、陀螺输出角速度随机误差和其他误差等效而成的陀螺零偏误差(为了方便分析这儿假设其为常值)。陀螺输出角速度随机误差主要由零偏不稳定性、角随机游走噪声和量化噪声组成,由于这类误差无法补偿,且不会引起规律明显的航向敏感误差,所以本文不对其进行误差分析。
3 航向敏感误差源分析
3.1 陀螺常值零偏影响分析

可见,旋转一周的等效东向陀螺零偏为

3.2 陀螺标度因数误差的影响分析
假设转位机构以角速率ω正向旋转,考虑地球自转角速率,则理想情况下,go系中陀螺敏感到的角速率ωgo为

考虑标度因数误差的影响,并将角速率测量误差转换到导航坐标系,则有


可知正转时等效东向陀螺误差为
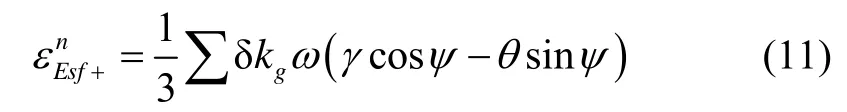
当转速为36 (°)/s,(δkgx+δkgy+δkgz)/3=10-6时,标度因数误差可以等效为0.1296 (°)/h的陀螺零偏,5°倾角时投影到东向的等效零偏约为0.01 (°)/h,会引起明显的航向敏感误差。由于陀螺标度因数标定误差及其本身漂移可以达到10-5,因此速率偏频寻北系统中不建议采取恒速偏频的方式,而采用正反连续偏频方案。反转时,有

从式(11)和式(12)可以看出,标度因数误差引起的等效东向陀螺常值零偏在正反旋转过程恰好正负抵消,也就是说若三轴陀螺的正反标度因数一致且正反旋转角速率一致,则经过正反整周旋转的调制作用,是不存在等效东向陀螺零偏的。
但是若陀螺正反转标度因数误差不一致,正转时三轴陀螺存在不对称标度因数误差δzfgxk、δzfgyk、δzfgzk,反转时存在不对称标度因数误差 δzfgxk-、δzfgyk-、δzfgzk-,令有:

两者相加得到:
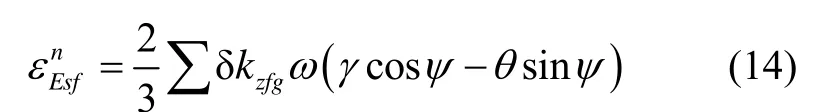
根据实际工程经验和推算,激光陀螺的标度因数不对称误差小于 10-7,若2δzfgxk=10-7,2δzfgyk=10-7,2δzfgzk=10-7,转速ω为 36 (°)/s,横滚角γ=0°,俯仰角θ=5°,那么投影到东向的等效常值零偏约为0.0011(°)/h,根据公式(5),纬度 53°地区方位ψ=90°有时相对真值的寻北均值误差为−25″,ψ=270°时的寻北均值误差为25″,造成明显的航向相关误差。
3.3 陀螺非正交安装误差影响分析
由于标定非正交误差的影响,激光陀螺测量输出的地理系角速率存在如下误差:

对式(15)整周积分,并且忽略非正交误差、水平姿态角和地球自转角速度三者相乘的高阶误差项,可以得到:

式(16)中第二项与文献[5]中结论是一致的,式(16)中忽略了地球自转角速度的影响。由于本文采用正反连续速率偏频方案,式(16)中的第二项误差实际上是可以完全抵消的。而对于式(16)中第一项,当纬度为53°,横滚角γ=0°,俯仰角θ=5°,σzy=σyz=σxz=20″时,在水平状态任意方位都会产生0.000 38(°)/h的等效水平陀螺零偏,进而产生8″的相对真值误差。
3.4 加计常值零偏影响分析

关于普及排印本古今字的辨析使用,应该根据词频统计,参照《现代汉语词典》等的收词情况,采取从俗的原则选用今字,而不能继续使用原字或古字。
3.5 加速度计标度因数误差影响分析
加速度计标度因数误差的分析与陀螺标度因数误差的分析类似,

经过整周期旋转积分,其等效比力误差为

可见加速度计标度因数误差不会产生等效东向加计零偏,因此不影响速率偏频系统的航向对准精度。
3.6 加速度计非正交安装误差影响分析
假设三轴加速度计存在非正交安装误差μzy、μyz、μxz,那么引起的地理系比力测量误差为
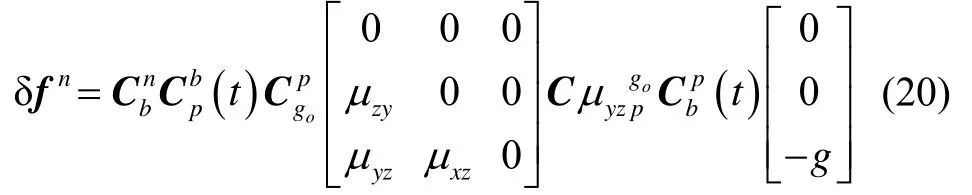

式(21)中认为非正交安装误差、水平姿态角都为小角度,忽略其三阶误差项,有

若加计非正交安装误差μzy=μyz=μxz=20″,横滚角γ=0°,俯仰角θ=5°,纬度为 53°,则ψ=0°航向均值误差为0.7″,ψ=90°时航向均值误差为3.5″,ψ=180°航向均值误差为−0.7″,ψ=270°航向均值误差为−3.5″。
3.7 航向敏感误差源分析总结和补偿方法
通过前文的误差分析可以发现,引起倾斜状态航向敏感误差的误差源主要为旋转轴方向的陀螺零偏误差和标度因数不对称性误差,其他误差源引起的寻北误差为小量误差或者非航向相关误差。
从式(7)和式(14)可以看出,无论是激光陀螺速率偏频相对机抖偏频的零位偏差还是标度因数不对称性误差,其对寻北精度的影响形式是一样的,并且都是可以补偿的,因此航向敏感误差的消除可以通过调整激光陀螺的旋转轴方向陀螺零偏实现。这种调整的目的就是为了抵消激光陀螺标度因数不对称性误差或者可能发生的速率偏频状态陀螺零位偏移量。当然,这种调整只在对准状态进行,当系统进入机抖偏频状态后,应该重新恢复原有标定零偏参数。
应该注意的是,从多套样机系统的试验数据来看,并非每套系统在补偿前都会出现倾斜状态下的航向敏感误差,这就说明激光陀螺标度因数不对称性误差和速率偏频状态的零位偏移并不是每支激光陀螺的共性。因此,并不需要对所有速率偏频系统笼统的使用上述方法进行补偿。另一方面,旋转轴方向陀螺零偏调整量的确定可以通过离线计算程序反复调整、反复计算直至航向敏感误差最小为止,一旦确定就可以将其作为固化参数烧写至系统内部,后续对准过程DSP软件可以自动调用和补偿。
4 试验验证
2017年2月10日采集了试验数据对速率偏频惯导倾斜状态航向敏感误差问题开始分析研究,利用陀螺零偏稳定性为 0.003(°)/h(1σ)和加计零偏稳定性为30 μg(1σ)的系统在精度为2″的转台上进行倾斜六方位对准试验,对准时间5 min,每个方位对准两次,共进行两次试验,其在线结果如表1所示。采用等效旋转轴方向陀螺零偏补偿措施,利用保存的试验数据进行离线计算,其寻北对准结果如表2所示。
从表1和表2中结果可以看出:未进行航向敏感误差补偿前,俯仰角−4.8°时的全方位对准精度为58″(3σ),俯仰角 4.5°时的全方位对准精度为 86″;进行航向敏感补偿后,俯仰角−4.8°时的全方位寻北精度为28″,俯仰角4.5°时的全方位寻北精度为36″,大幅提升了全方位对准精度。2017年6月25日在完善该方法后对其进行了更加全面的验证,利用同一补偿参数,在横滚角3.0°和俯仰角-6.2°时对该方法进行在线验证,其结果如表3所示,可以看出两种倾斜状态下的寻北精度都优于 30″,说明补偿量的大小与水平倾角无关,补偿结果与误差理论分析结论相符。

表1 补偿前的倾斜全方位对准结果Tab.1 Test results of tilted-state multiple-azimuth alignment before compensation

表2 补偿后的倾斜全方位对准结果Tab.2 Test results of tilted-state multiple-azimuth alignment after compensation

表3 其他倾斜角度下的全方位对准验证试验结果Tab.3 Validation test results of multiple-azimuth alignment with other dip angles
5 结 论
从速率偏频系统模型和对准精度公式出发,分析了各误差源对速率偏频系统寻北精度的影响,明确了引起倾斜状态航向敏感误差的主要因素,提出了以调整激光陀螺旋转轴方向陀螺零偏抵消激光陀螺标度因数不对称性误差或者速率偏频状态陀螺零位偏移的航向敏感误差补偿措施,经试验验证,该措施简单有效,大幅提高了该系统的全方位寻北精度。

