基于三维空间椭球概率误差的落点精度评定方法

魏宗康，高荣荣，周 姣，江 麒

（北京航天控制仪器研究所，北京100854）

在惯性导航与制导系统和弹道导弹武器系统中，由于受惯导和武器系统的性能以及外部复杂的环境等因素的综合影响，导弹在空中可能分布的落点多呈现出沿不同方向不均匀散落的分布统计特征。对空中散布的落点进行精度评估建模与分析，是评估导航系统和武器系统实际导航与作战能力的一项非常重要的指标，对惯导和武器系统的装备改进和进一步作战手段的提升具有一定的指导意义和实践价值[1-2]。

针对三维空间中的导弹落点精度评估问题，目前的方法大多是将三维信息折合成二维，即降维处理，存在信息缺失问题，因此无法精确表征导弹等在三维空间的落点精度估计情况[3-5]。

现阶段用于描述空中导弹系统落点精度的方法最常用是球概率误差（SEP, Spherical Error Probable），即落点位置落入以散布中心为球心的某个球内的概率为50%时的圆球的半径R称为SEP。SEP方法对于落点在空中三个方向近似均匀分布的情形是一种非常好的评估手段[6-7]，但是在实际导弹打靶时，落点的分布呈现出在不同方向上分布不均匀性和方向相关性等问题。其中，涉及落点位置标准方差不等，即落点在各方向上分布不均匀，文献[8]中并没有给出详细且精确的表达式结果，只给出了基于 Grubbs方法的近似计算式。

此外，针对落点分布相关性的问题，大多数文献只给出了将落点相关转为落点不相关的数学转化方法，并没有直接给出落点位置标准方差相关时的精度估计的一般经验表达式。另外，这种独立性转化的方法只是纯数学转化，无物理意义，即无法表征误差模型在三维空间落点相关时的实际空间位置。因此，目前解决相关性问题的方法不够直接、实用，不能作为一般性的结论推广。

针对二维精度评估方法精度表达有限、三维精度评估方法较为简略、表述模糊、不完善以及在落点方向相关性和方向不均匀性等问题上没有给出明确的精度估计表达式等问题，本文提出了一种基于三维空间的椭球概率误差ESEP落点精度评估方法，并给出了不同情形下的椭球概率误差一般性表达式。三维空间的椭球概率误差模型可充分展示导弹落点在三维空间中更多的导航误差精度分布特性，且弥补了二维精度的信息缺失问题和三维球模型的精度表达过于简单的问题。

1 等标准误差和零均值的球概率误差SEP

空间中的落点位置误差用三维坐标表示，设r=(x,y, z)为落点位置误差的三维向量表述。大量的导弹落点由大数定律知，其在整体上服从正态分布且相互独立，即其联合概率密度函数为

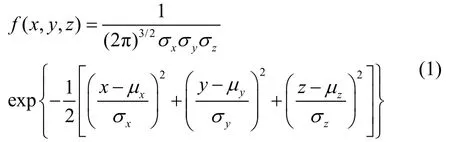
同时，

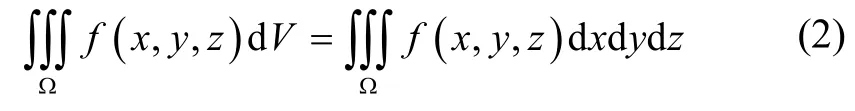
式中，μx、μy、μz分别为三维方向落点中心，σx、σy、σz分别为三维落点位置标准方差。

首先，我们研究当三个方向标准方差相等且独立、均值为零时的情况，即为了使运算过程简便，我们将繁琐的数值积分运算转换为球坐标形式，令：

此时，有：

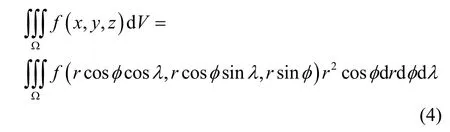
概率积分变成：

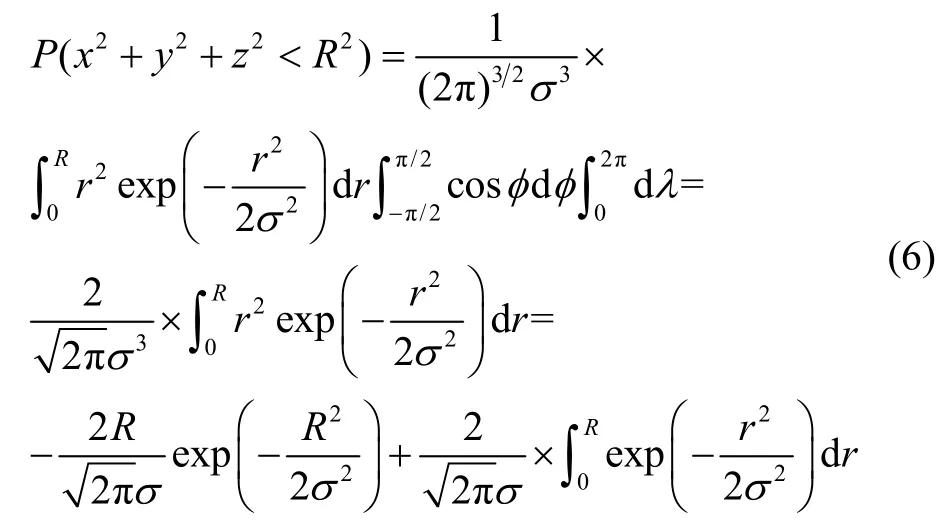
针对式(6)积分没有精确表达式的情况，一种方法是将指数函数近似展开为迈克劳林函数进而得到SEP的近似值，但是这种方法在展开阶数n非常大时才能得到一个较为接近真值的近似值[9]。另一种方法是将不能直接积分部分转化为标准正态分布函数，进而利用标准正态函数分布表得到球径R与标准方差σ之间的近似关系。

本文对式(6)进行重复积分运算，得到R/σ与概率P(x2+ y2+ z2＜R2)的变化规律关系图，如图1所示。从图中可以看出，在R/σ=1.539时，P(x2+ y2+ z2＜R2) =0.5。从而得到R的近似表达式R=1.539σ。选取以上落点位置标准方差为仿真数据，建立导弹落点仿真模型，模拟打靶5000发，得到落点分布和圆球概率误差模型分别如图 2中蓝点和红色区域所示。由此可见，R=1.539σ表达式在当落点呈等标准差独立分布、零均值时，在三维球概率误差精度评定指标体系中具有重要的指导作用。

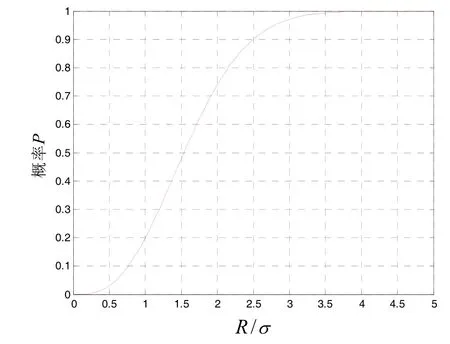
图1 概率P分布与R/σ关系Fig.1 Relationship between R/σ and probability

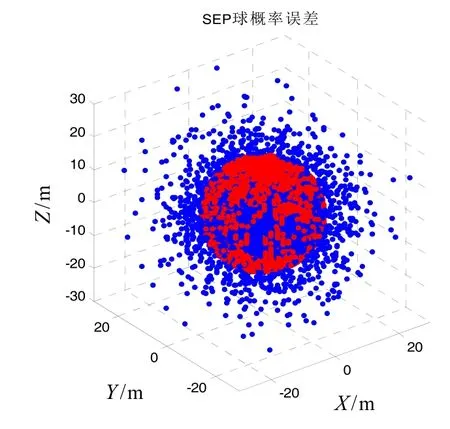
图2 等标准误差和零均值的球概率误差模型Fig.2 Spherical Error Probable model with equal standard error and zero mean

2 非等标准误差及零均值的椭球概率误ESEP

我们在第1节得到了落点在三个方向上的等标准方差时的SEP一般表达式。在实际导弹射击中，落点在空间中的散布情况并非在三个方向上均匀分布，而是有一定的方向性，主要表现为在每个方向上分布的不平衡性[10-11]。因此，我们需要对非等标准误差的情形进行分析，并得到其精度评估的一般表达式。

首先，假设σx≠σy≠σz，μx=μy=μz=0。为了运算简便，仍采用球坐标形式，令：

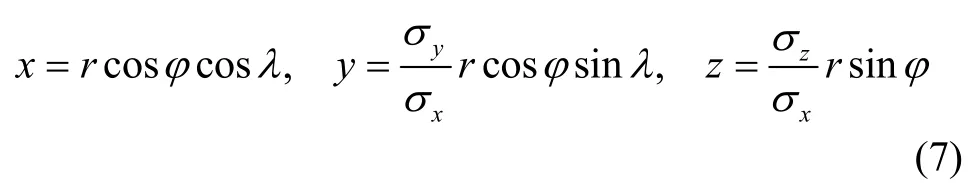
其中，2πλ0≤≤，π/2π/2φ-≤≤。

将极坐标形式的三个变量带入到式(2)中，有：

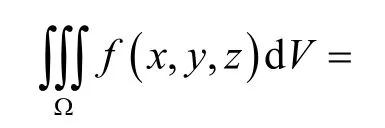
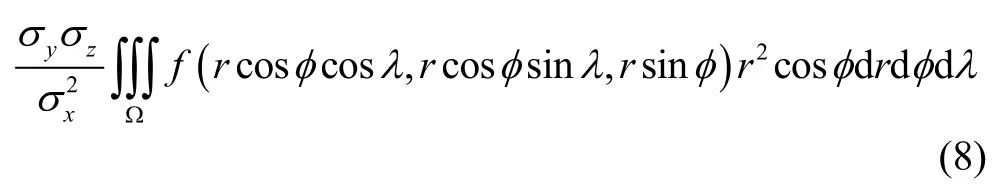
概率积分变成：

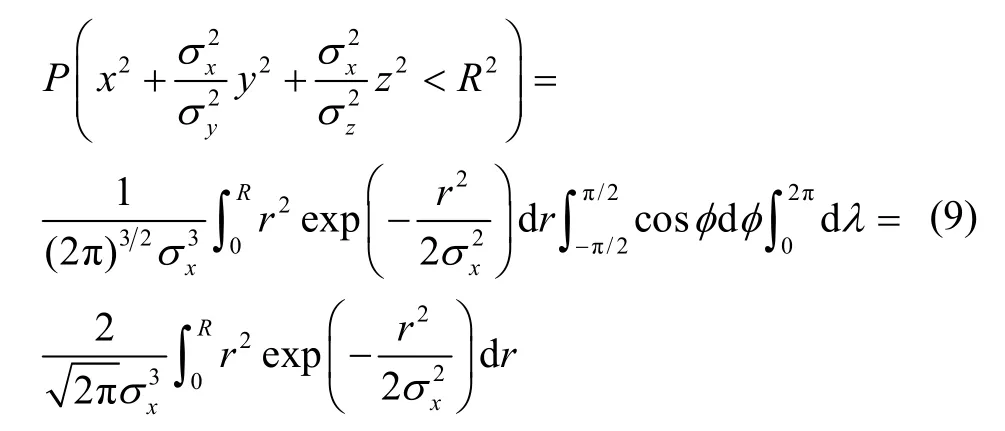
由积分结果看出，与等标准误差和零均值的SEP的表达方式完全相同，即当R=1.539σx时，有：

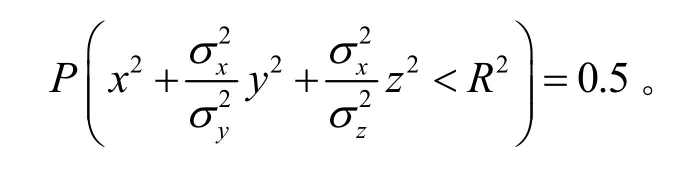
由此计算得出椭球体的 X轴半径的长度为a=1.539σx，Y 轴半径的长度为 b=1.539σy，Z 轴半径的长度为 c=1.539σz。综上所述，用椭球表示的三维空间落点精度为 ESEP=(1.539σx, 1.539σy, 1.539σz)。

某型号导弹落点仿真为例，模拟打靶5000发，落点分布如图3中蓝点所示。由于三个方向落点位置误差的标准差不相关，假设沿X、Y、Z轴落点位置分布的标准差分别为σx=100 m、σy=200 m、σz=300 m。根据椭球概率误差模型得到 ESEP=(153.9 m, 307.8 m,461.7 m)。即椭球的X半轴为153.9 m，Y半轴为307.8 m，Z半轴为461.7 m，仿真得到非等标准方差椭球概率误差模型如图3中红色部分所示。基于Grubbs方法近似估计求得的球形半径R= 313.5705 m，在不同平面上椭球概率误差模型和球概率误差模型分别如图4中红色部分和绿色部分所示。由椭球概率误差可以看出，沿X轴方向导弹有50%的概率落在153.9 m以内，而沿Y轴方向导弹偏离中心的距离相对更远，有50%的概率落在307.8 m的范围内，导弹落点在X轴方向比Y轴方向更为密集。相比于圆球在 OXY平面的投影，椭圆更加清楚、准确地表达了导弹落点在不同方向分布的不平衡性，精度估计更加准确。同理，OYZ和OXZ平面的投影效果与OXY平面类似，不做分析。

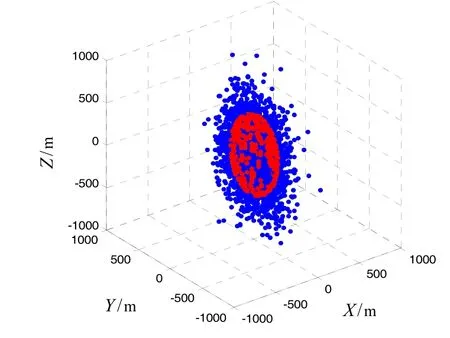
图3 非等标准方差的椭球概率误差模型Fig.3 Ellipsoid Error Probable with unequal standard error and zero mean

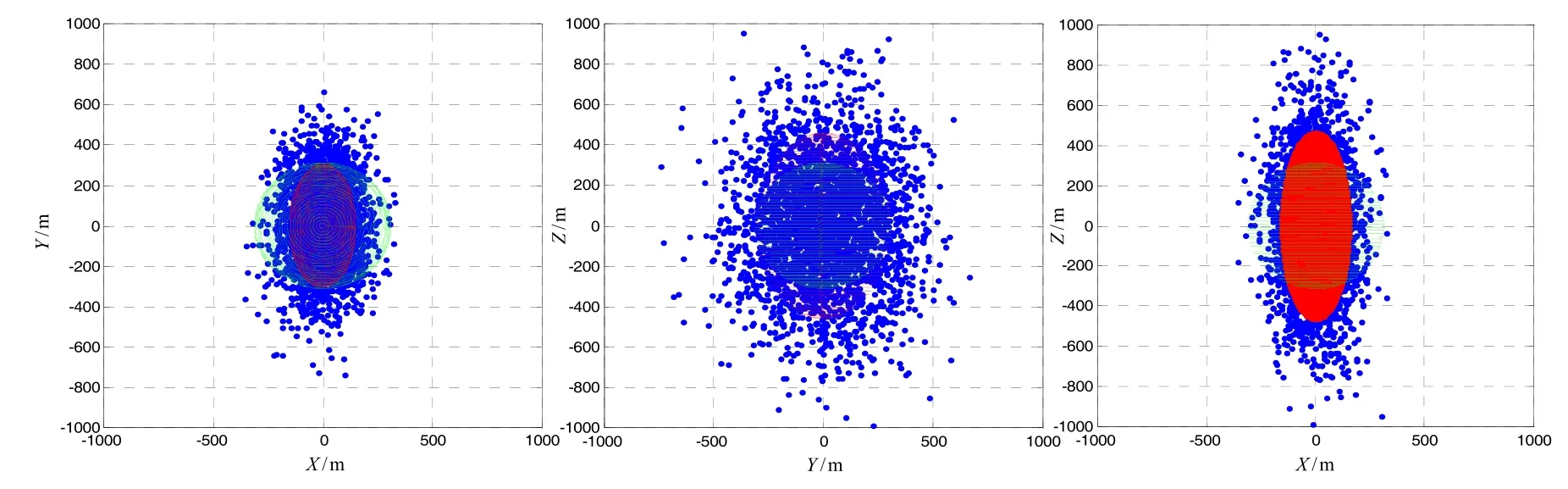
图4 OXY、OYZ和OZX投影下ESEP与SEP对比Fig.4 Comparison between Ellipsoid Error Probable and Spherical Error Probable in OXY, OYZ and OZX planes

此外，该椭球体的体积与半径为 1.539(σxσyσz)1/3的圆球的体积相等，意味着能覆盖50%的落点的所有立体图形中该椭球体的体积最小，能更精确表达导弹落点分布的密集度。例如，基于Grubbs方法求得的半径R=313.5705 m，其圆球体积为12.915×107m3，而由ESEP模型求得的椭球体积为 2.5133×107m3，近似球形体积与椭球体积相比，相差5倍, 因此，椭球在精度评价中能够更加精确地表示落点精度的密集度。

3 相关系数非零时的椭球概率误差ESEP

在实际的导弹射击过程中，由于导航系统的偏差以及外部环境因素等的综合影响，真实导弹落点分布通常存在方向相关性问题，即X轴、Y轴和Z轴方向落点位置标准方差相关，使得落点在三个直角坐标轴上的分布呈一定的角度。因此，当导航精度评价较为严格的情况下，落点间的相关性成为了精度评估中必须要考虑的因素。

为了解决落点位置标准方差相关的问题，我们通过坐标轴旋转的方式，将相关性问题转为不相关。在美国艾佛里尔的《高精度惯性导航基础》一书中，作者认为由于位置协方差矩阵是对称的，计算独立分布条件下的椭球概率误差模型可通过分别旋转两次坐标轴获得，即假定第一次绕原始坐标系OXYZ的Y轴旋转β角，第二次绕负Z轴旋转θ角。

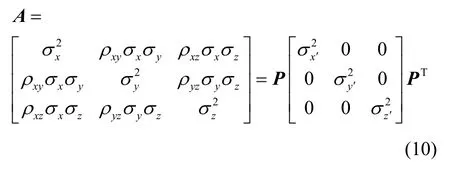
通过旋转矩阵将相关的协方差矩阵转为不相关，从而得到位置标准方差不相关时的对角矩阵，即其中，xσ′、yσ′、zσ′分别为变换后不相关的位置标准方差，ρxy、ρyz、ρxz为相关系数。

在对《高精度惯性导航基础》书中的椭球概率误差计算方法和模型进行复算和检验时发现，θ 的求取受到两个约束条件限制：

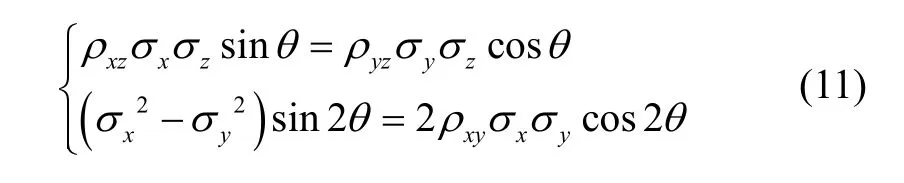
即

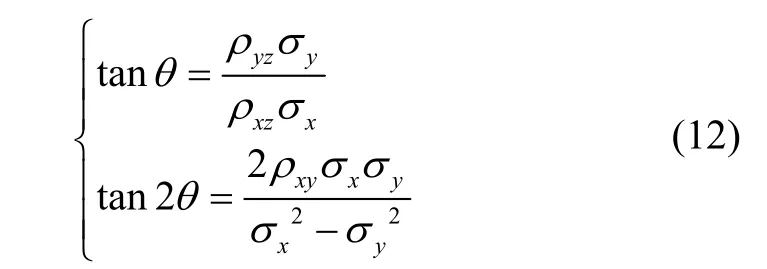
式(12)意味着系数之间增加了一个约束条件：

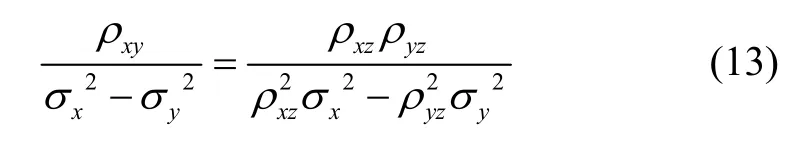
以σx=100 m、σy=200 m、σz=300 m，ρxy=0.5、ρxz=0.5、ρyz=0.5为例，按照求解得到但这说明不存在一个θ使得这种约束条件成立，同时也导致落点标准方差不唯一。因此，通过两次旋转计算相关系数非零时的椭球概率误差方法存在缺陷。

为了解决上述问题，我们采用了三次坐标轴旋转的方法，即增加一个约束使得落点标准方差唯一。假定第一次绕原始坐标系OXYZ的Y轴旋转φy角，第二次绕负X轴旋转φx角，第三次绕负Z轴旋转γ角，由此得到的新旋转变换矩阵P如下：

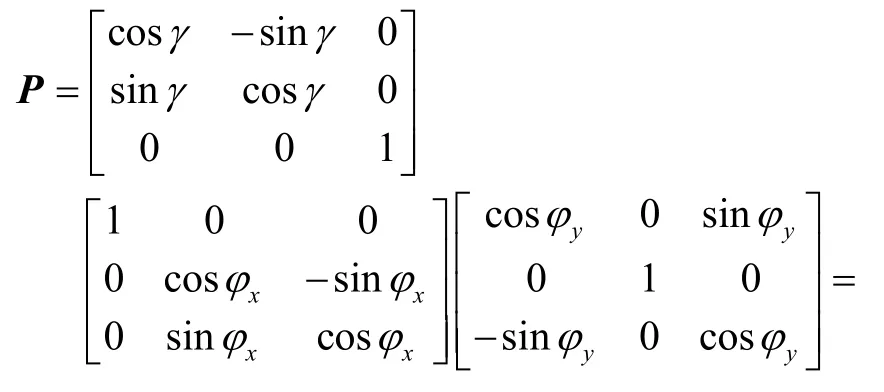
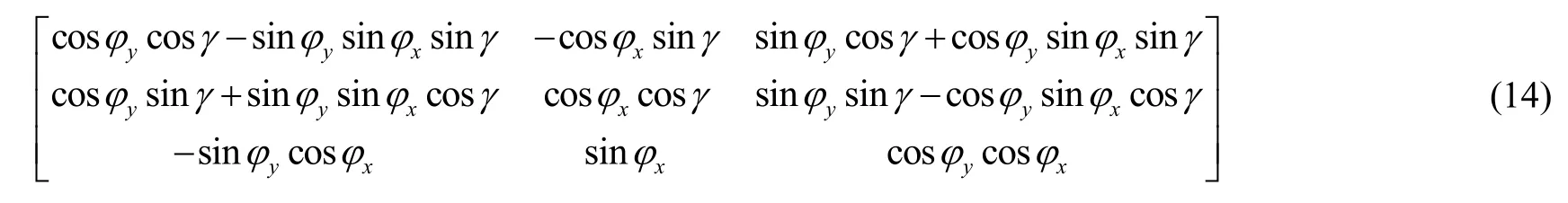
将式(14)所示P阵带入到式(10)中，通过三次旋转将相关条件下的协方差矩阵转换为非相关，得到的位置标准方差对角矩阵分别为

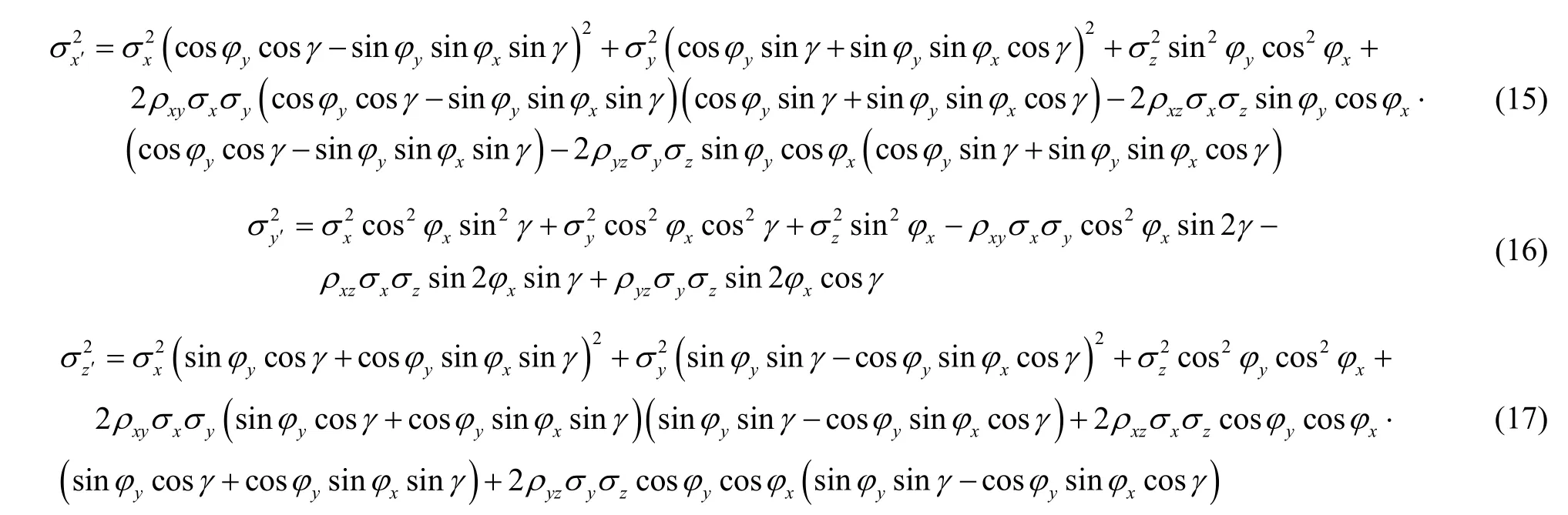
令非对角线元素为零，解两个完全相同的非对角线项之一，得到式(18)，由此解得角φx和角γ。

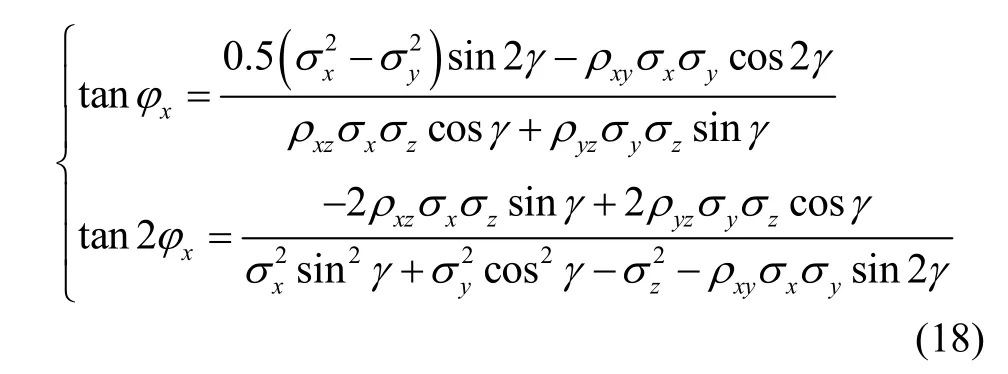
求解式(18)，可采用迭代方法精确求解，此处选取牛顿迭代法。

首先，根据tanφx和tan2φx之间的三角函数关系，可定义以下函数：

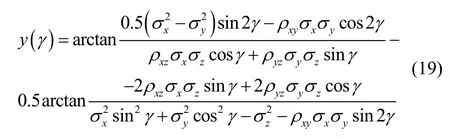
选取初值γ=0，利用牛顿迭代公式(20)可精确求解出γ值，进而得到φx。

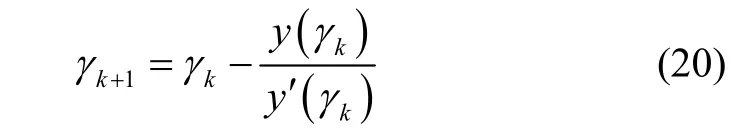
在解出φx和γ后，φy由式(21)求解：

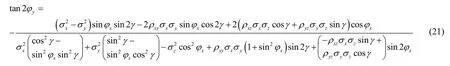
在坐标系OX′Y′Z′中绘制椭球，该椭球的三个半径分别为1.539xσ′、1.539yσ′和1.539zσ′，由此可得新坐标系下的椭球模型，如式(22)所示：

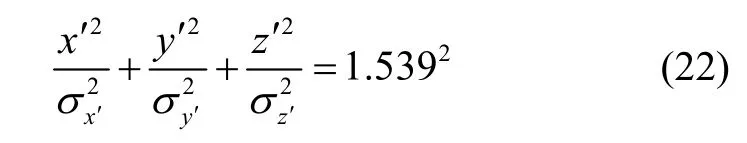
把该椭球从坐标系OX′Y′Z′中变换到OXYZ坐标系中，变换公式为

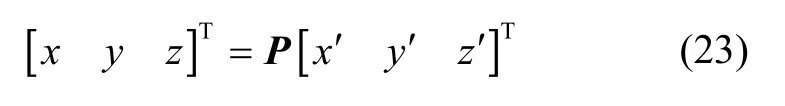
该椭球的体积为

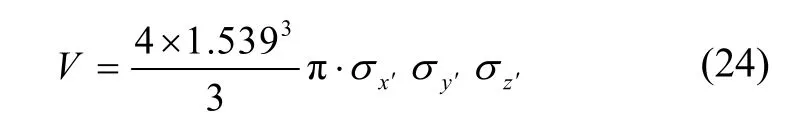
通过上述过程的分析，本文给出了一种在OXYZ坐标系中内通过六个参数(1.539xσ′,1.539yσ′,1.539zσ′,φx, φy, γ)描述一个覆盖了50%的落点概率的椭球，这六个参数定义为六参数描述的椭球概率误差ESEP。

以某型号导弹落点仿真为例，其中，σx=100 m、σy= 200 m、σz=300 m，ρxy=0.5、ρxz=0.5、ρyz=0.5，模拟打靶5000次，落点分布如图5中蓝点所示。由六参数椭球概率误差模型得到的6个参数分别为xσ′=79.8513、yσ′=162.1868、zσ′=327.5961、φx= -26.5828°、φy=6.6916°、γ=-8.4165°。由以上数据为例，采用式(24)计算得椭球的体积为6.48×107m3；采用基于Grubbs的方法计算得到的圆球体积为1.73×108m3，两者相比，明显六参数椭球概率误差方法得到的体积最小。在坐标系OXYZ中表示的椭球如图5中红色区域所示。其中，落点与椭球分别在OXY、OYZ和OXZ平面上的投影如图6所示。

经实验统计，此六参数的椭球概率误差模型共有2493个落点在椭球内，有2507落点在椭球外，验证了此模型的正确性。

最后，我们采用正交矩阵变换的方式来验证三次旋转下的落点位置标准方差的一致性与唯一性。落点位置标准方差协方差矩阵A是实对称矩阵，由数学理论知，其一定存在一个正交矩阵Q使得QAQT=Λ。Λ是一个对角矩阵，即对角元素为协方差矩阵A的特征值，且唯一，同时也是落点位置的方差。同样以σx=100 m、σy=200 m、σz=300 m，ρxy=0.5、ρxz=0.5、ρyz=0.5为例求解得到此结果与通过三次旋转矩阵P得到的落点位置标准方差一致。

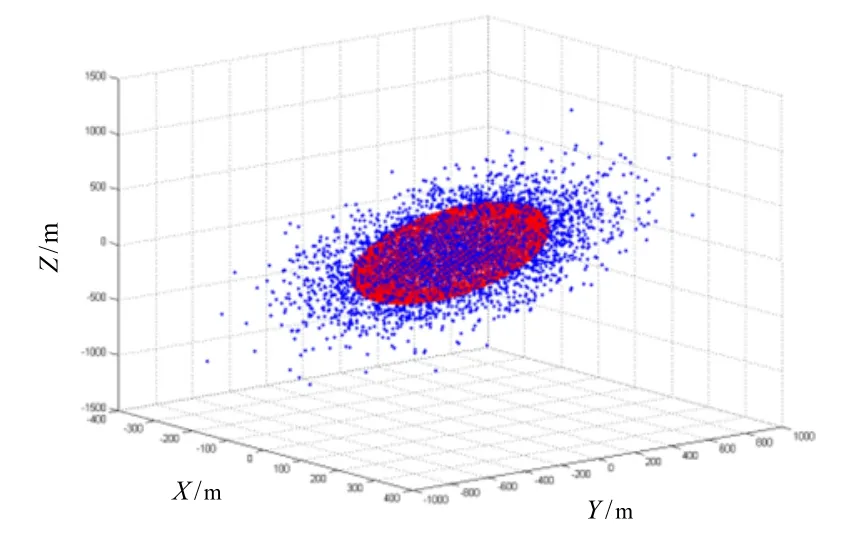
图5 在OXYZ中六参数椭球概率误差模型Fig.5 Six-parameter Ellipsoid Error Probable model in OXYZ coordinate system

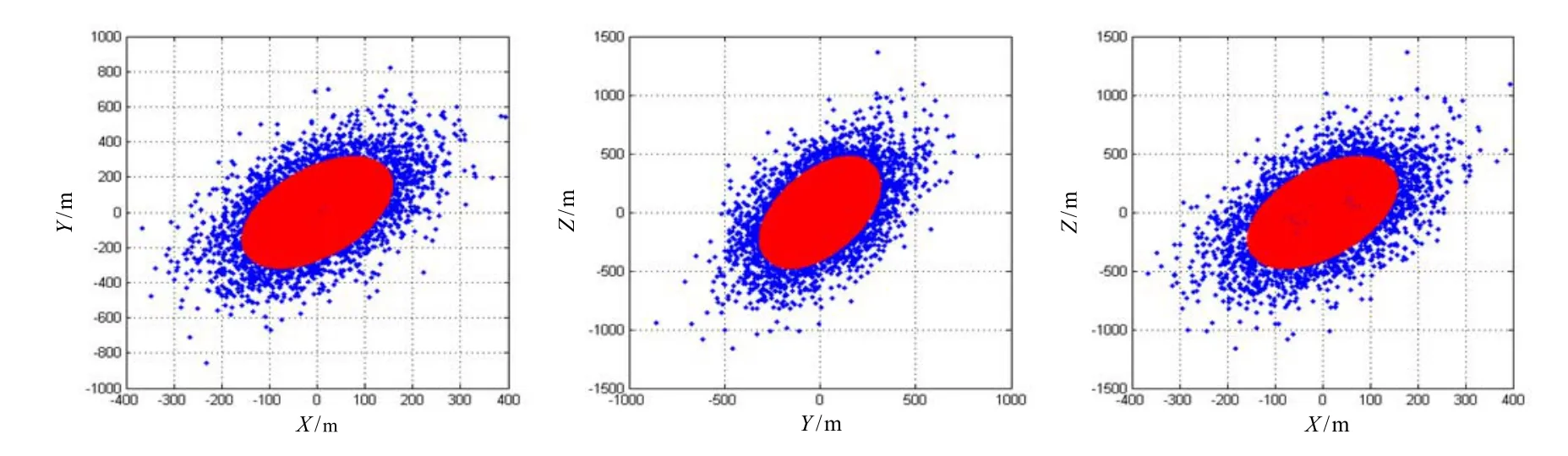
图6 在OXY、OYZ和OXZ平面内落点及椭球的投影Fig.6 Ellipsoid Error Probable model in OXY, OYZ and OZX planes

4 结 论

本文针对三维空间领域导弹落点精度评估方法单一、不精准以及无通用表达式等问题，通过分析导弹落点在空中的分布情形，给出了一种三维椭球概率误差精度评定方法。该方法针对三维空间中落点在不同方向上存在不均匀性和方向相关性等特征，通过三次坐标轴旋转矩阵将相关转化为非相关，并且经分析验证，与正交变换所得的特征值比较，三次旋转下的六参数椭球概率误差模型的位置标准方差唯一。此外，由于||P||=1，可以得出通过旋转所得椭球，其形状并未发生改变，并且所得椭球体积最小。因此，该方法能够更准确、直观地描述空中落点在不同方向的差异性及方向相关性，对弹道导弹和惯性导航与制导系统在三维空间中的落点精度评估具有非常好的实际指导意义。