空间不一致在动态对准中影响分析及补偿方法

李 杨，孙伟强，王兴岭，赵凤昊

（1.海军研究院，北京 100161；2.天津航海仪器研究所，天津 300131）

在惯性导航系统的对准及组合导航应用中，时间以及空间的一致性对系统有着重要影响。文献[1]研究了两套激光陀螺惯组之间的时间同步对船体变形测量的影响，对于舰载惯导系统初始对准来说，滤波周期较长，可以利用卫导同步脉冲来进行惯导与卫导之间的同步。对空间不一致的影响，一般称之为杆臂效应问题，研究大都集中在舰载或机载惯导在以舰载主惯导提供的速度或姿态信息为基准进行传递对准时如何进行杆臂效应的补偿，如文献[2-4]对传递对准过程中杆臂的估计及补偿进行了较为深入的研究，文献[5]还对传递对准过程中杆臂的变形进行了研究。除了在传递对准过程中的杆臂效应外，还有针对惯性测量组件非质点的特点进行的尺寸效应研究，文献[6]对弹载惯组的内杆臂效应进行了补偿，有效提高了弹体攻击精度。文献[7]针对载体晃动时由于杆臂效应引起的速度波动，设计了杆臂补偿方式，提高了系统粗对准精度。文献[8]从频域的角度出发，设计了弹载惯组低通滤波算法，以消除杆臂效应在晃动时引起的速度波动，提高弹载惯组初始对准精度。

从以上文献分析，目前针对空间不一致对系统影响都集中在以速度或姿态匹配方法上，对于采用惯导/卫导进行位置匹配初始对准时空间不一致的影响研究甚少。针对这一问题，本文对采用位置匹配初始对准算法中的空间不一致的影响及补偿方法进行了研究，推导了以位置为匹配信息时的杆臂补偿方程，并进行了半实物仿真。

1 位置匹配初始对准原理

粗对准得到惯导系统的粗水平和粗航向，与真实值之间存在失准角，惯导系统输出的位置参数与卫导位置之间存在差值，位置匹配初始对准就是基于这一原理，利用位置误差信息，建立相应的系统模型，通过卡尔曼滤波估计出失准角，达到初始对准的目的。根据参考文献[9]，直接给出系统的状态方程为：

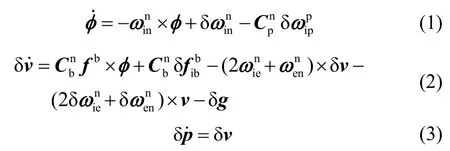
系统的观测方程见式(4)：

其中，H为观测矩阵，与观测量对应的值为1，其余值为0，X为选取的状态矢量。

2 空间不一致误差分析及补偿

如图1所示，定义导航坐标系为OXnYnZn，载体坐标系为 OXbYbZb，从舰船中心平移至惯性导航系统中心，卫导接收天线所处位置的坐标在载体坐标系的投影为（xb, yb, zb）。在载体坐标系中，卫导接收天线相对惯性导航系统的位置是不变的，其在导航坐标系的投影（xn, yn, zn），随着载体姿态、航向的变化而变化。卫导接收天线坐标在导航坐标系投影与在载体坐标系投影关系见式(5)：

舰船直航时空间位置差在导航坐标系中的投影是常值，不会对初始对准结果产生影响。当舰船转向时，系统可观测度提高，卡尔曼滤波器收敛速度加快[10]。同时，根据式(4)和式(5)，空间位置差在导航坐标系的投影发生变化会在观测量中引入误差，影响卡尔曼滤波估计效果，导致初始对准结果变差。因此，初始对准阶段大都对舰船运动做出限制，要求直航运动，但实际舰船很难保持直航运动。

图1 空间不一致示意图Fig.1 Sketch map of space dimension

根据式(5)，卫导相对惯导的空间位置差投影到导航坐标系后，xn指南北向，影响纬度误差，yn指东西向，影响经度误差，zn指天向，影响垂向误差。根据观测方程式(4)，可以得到空间位置差补偿方法，由于卫导位置坐标单位为m，需要转换成与经纬度相同的单位rad，则观测方程空间不一致具体补偿公式见式(6)：

3 半实物仿真实验与分析

为了验证空间不一致补偿的分析，采用位置匹配的卡尔曼滤波精对准算法，利用舰载实验数据进行半实物仿真分析。数据全长9 h，其中初始对准1 h，导航8 h。惯导为某型激光陀螺纯捷联系统，卫导型号是Novatel DL-V3，定位精度1.8 m（RMS）。以惯导中心为原点，卫导接收天线的坐标点为（−5.2, −22.1, 6.0），坐标点单位为m。状态变量取三维姿态角误差、三维速度误差、三维位置误差、三维加速度计零位和三维陀螺仪常值漂移共15个变量。

观测矩阵H为：

卡尔曼滤波具体实现较简单，具体公式见参考文献[9]，本文仅给出仿真时P、Q、R阵的取值。

P阵初始值取为：

系统噪声矩阵Q：

观测噪声矩阵R：

图2给出了船近似直航初始对准的航向角、东速误差、北速误差、纬度误差和经度误差。从图2(a)可以看出，对准期间，载体并没有大的转向，只存在一定幅度的摆动，从图2(b)中可以看出，对准结束时刻，补空间不一致和未补空间不一致两者航向相差约0.027′。从图2(c)中可以看出，未补偿空间不一致的速度误差在刚转导航时有较大波动，而补偿空间不一致后，速度误差波动基本被消除。从图2(d)中可以看出，两者纬度误差相差不大，这也符合图(b)中两者航向相差不大的现象。从而可以得出结论，在载体无大的航向变化时，补偿空间不一致对系统精度提高并不是很明显。

图3给出了船转向170°初始对准的航向角、东速误差、北速误差、纬度误差和经度误差。从图3(a) 可以看出，对准期间，载体大部分时间处于直航状态，在对准约45 min，转向约170°。从图2(b)中可以看出，对准结束时刻，补空间不一致和未补空间不一致航向相差约 4.3′。从图 2(c)的补空间不一致和未补空间不一致的速度误差对比可以看出，未补偿空间不一致的速度误差波动很大，补偿空间不一致的速度误差较平滑。从图2(d)可以看出，未补空间不一致纬度误差最大达到了约 4.5 nm，而补偿空间不一致后纬度误差最大值约0.5 nm。从而可以得出结论，对准阶段载体有较大转向时，需要补偿空间不一致，以提高系统初始对准精度。

图2 对准阶段近直航仿真结果Fig.2 Simulation results when sailing almost straightly during initial alignment

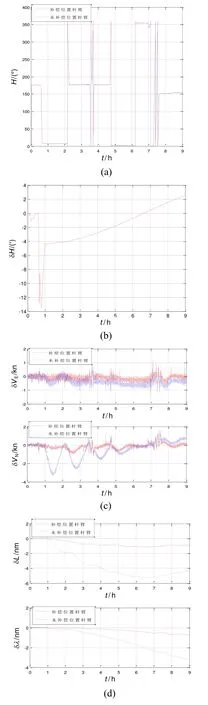
图3 对准阶段转向170°仿真结果Fig.3 Simulation results when head turns to 170°during initial alignment

4 结 论

本文对位置匹配初始对准时空间不一致的影响进行了分析，给出了空间不一致补偿方法，并进行了半实物仿真。通过分析可以得到以下结论，对于惯导与卫导天线安装在一起的载体，空间不一致补偿对对准结果影响不大。但在惯导与卫导天线安装位置相差较远的载体上，对空间不一致进行补偿是非常有必要的，补偿空间不一致误差后，能够有效降低初始对准阶段对载体机动的要求，提高载体机动适应性。