基于矩阵卡尔曼滤波的捷联惯导初始对准算法

崔 潇，秦永元，严恭敏，周 琪

（1.西北工业大学 自动化学院，西安 710129；2.西安飞行自动控制研究所，西安 710065；3.飞行器控制一体化技术国防科技重点实验室，西安 710065）

SINS的初始对准问题实质就是一个姿态确定问题，基于观测矢量的姿态确定方法是常见的对准方法。1965年 Wahba将姿态确定问题描述为带约束的最小二乘估计问题，即Wahba问题。随后产生了诸多基于矢量观测求解姿态的算法，根据算法实现方式的不同，基本可以分为两类[1]：一类是解析姿态计算算法，这类算法利用两个或多个观测矢量直接确定最优姿态，即根据同一矢量在不同坐标系中的投影来反向解算姿态，如基于双矢量的 TRIAD算法和基于多矢量观测求解 Wahba问题产生的 q-method、QUEST、 ESOQ和ESOQ2等算法[2]；另一类算法称为状态估计法，一般需要通过姿态动态方程跟踪姿态的连续变化，综合利用各历史观测矢量数据进行姿态确定或修正，其中最常用的就是基于“预测+修正”思想的卡尔曼滤波方法，根据动力学模型建立误差方程，从而对姿态参数和相关误差源进行实时估计和补偿[3]。

静基座条件下，惯导初始对准以重力加速度和地球自转角速度为参考，利用陀螺和加速度计输出直接解析法完成对准；在晃动条件下则借助于重力矢量在惯性空间的投影特征间接完成对准[3-4]。而针对晃动基座大失准角条件下的对准，目前主要采用基于失准角[5-7]、罗德里格参数[1,8]等作为估计状态，建立非线性对准模型，利用诸如 UKF[6-7]、EKF2[1,8]、CKF[9]等非线性估计方法实现对准，但存在状态初值及滤波参数选择的问题。

本文摒传统大失准角对准思路，借鉴传统REQUEST算法[10-12]，直接以对准起始时刻的姿态对应的K矩阵作为估计目标。将重力矢量在惯性系下的投影作为量测，利用矩阵卡尔曼滤波（MKF）对初始姿态对应的K矩阵进行估计，这样就可完成惯导系统在晃动条件下的初始对准。与传统算法相比，该算法避免了对于失准角大、小的假设，建立了基于K矩阵的线性矩阵卡尔曼滤波对准统一模型，对准过程不再区分粗、精对准，即可实现任意姿态初值条件下的初始对准。

1 惯性系初始对准

1.1 惯性系对准原理

为了解决摇摆基座下的对准问题，采用惯性系下基于重力加速度积分的解析对准算法[12]（本文简称惯性系对准），巧妙地应用惯性凝固假设，将对准问题间接转化为常值姿态矩阵的确定问题。图1给出了惯性系初始对准的基本原理。

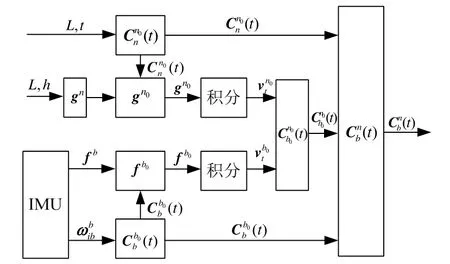
图1 惯性系对准原理图Fig.1 Alignment principle in inertial frame

根据姿态矩阵链式分解，载体的实时姿态可计算如下：

其中，n为导航坐标系，各轴向与当地地理坐标系的坐标轴重合； n0为导航惯性坐标系，将导航坐标系n在对准开始时刻相对惯性空间凝固所得的惯性坐标系；b为载体坐标系；b0为载体惯性坐标系，将载体系b在对准开始时刻相对惯性空间凝固所得的惯性坐标系。

1.2 惯性系REQUEST对准算法

REQUEST算法[12]的核心是递推求解 4维K矩阵。

选择比力一次积分作为观测矢量，即：

根据tk时刻的观测量bk、rk计算K矩阵增量δK：

其中，

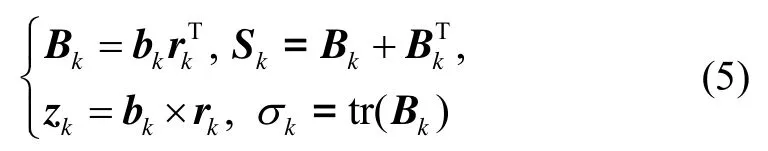
更新 tk时刻的 Kk矩阵：

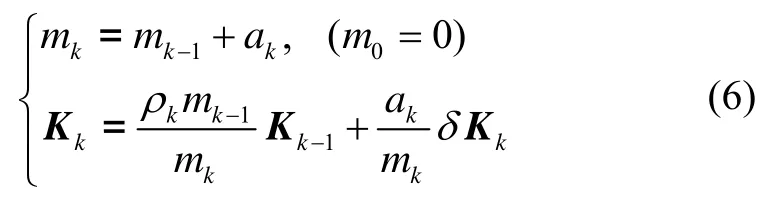
式中，ρk为退化因子，ak为tk时刻的观测量的权重系数。求解 Kk矩阵最大特征值对应的特征向量，即可获得初始状态矩阵根据式(1)计算当前姿态矩阵。实际上，由于ρk选择的随机性和权重系数ak的选取方式都将使得REQUEST算法为次优估计。

2 基于K矩阵的矩阵卡尔曼滤波对准模型

2.1 一般矩阵状态空间模型

一般的矩阵形式线性状态模型如下：

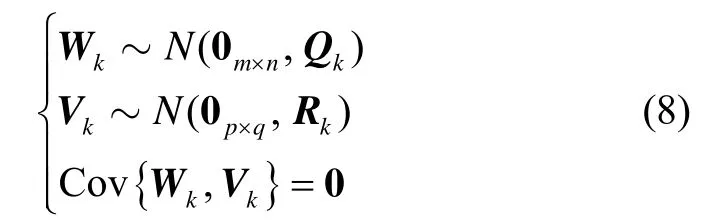
由式(7)不难发现，当状态Xk和量测 Yk均为向量时，即n=q= 1，式(7)就退化为标准的向量卡尔曼滤波模型。因此，向量卡尔曼滤波可以看作是矩阵卡尔曼滤波的特殊形式，利用向量卡尔曼滤波已有理论可完成对矩阵卡尔曼滤波的推导。可见，推导矩阵卡尔曼滤波基本方程，有三个步骤：矩阵模型向量化、向量化滤波方程推导和向量化滤波方程还原矩阵形式。

要将式(7)矩阵状态空间模型向量化，首先定义如下向量化算子：

若定义⊗为Kronecker积，则有如下向量化特性

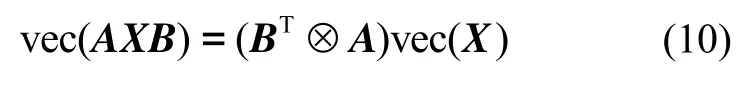
对式(7)中系统状态进行向量化操作，并结合式(10)，得：

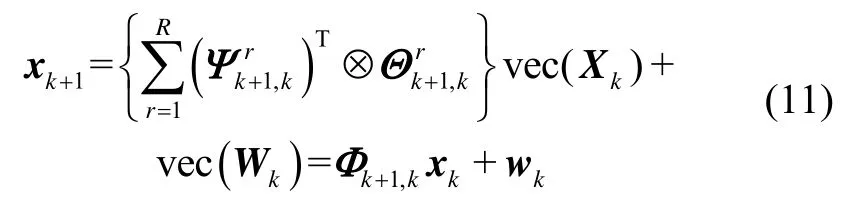
其中，

式(11)即为矩阵状态方程的向量化表示，根据标准卡尔曼滤波可得状态一步预测为

利用算子vec的线性特性和式(10)，则式(13)可等价于

一步预测均方误差：

根据式(7)记量测一步预测为：

残差为

对式(17)进行向量化，得：

则对于向量化之后的系统模型，由标准卡尔曼滤波可得：

其中，

为了将式(21)恢复到矩阵形式，引入如下定理：对于给定的矩阵且定义分别为矩阵Z和X向量化的向量，即将矩阵A写成如下分块矩阵的形式：

等价于如下矩阵方程：

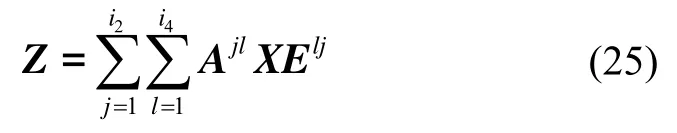
则将此定理应用于式(21)右端第二项，其余项利用向量化算子的逆运算，则

由标准卡尔曼滤波理论，矩阵估计均方误差为

式(14)(15)(17)(19)(20)(26)(28)即为矩阵卡尔曼滤波的基本方程。矩阵形式的卡尔曼滤波详细的推导和证明见文献[13]。

2.2 滤波模型

借鉴惯性系REQUEST算法，将传统解析对准同滤波对准结合，利用矩阵卡尔曼滤波（MKF）对K矩阵进行估计，这样就可完成惯导系统在晃动条件下的初始对准，而且可适用于任意失准角条件下的初始对准，对准过程不再区分粗对准和精对准。

由惯性系对准算法原理可知，所求对准初始时刻的姿态矩阵在整个对准过程中具有常值特性，故若以其对应的矩阵K作为待估计状态，则状态空间模型非常简单而且不存在模型误差：

其中 Kk分别表示 tk初始姿态四元数对应的K矩阵。

用ΔKk+1表示 tk+1时刻利用观测向量计算的K矩阵，也即量测矩阵，则K矩阵量测模型为：

表示 tk+1时刻利用无误差观测向量构造的

理想K矩阵； Vk+1表示量测噪声。

假设 tk+1时刻获得了一系列向量簇：

则式(30)中4×4对称量测噪声矩阵Vk+1为

其中，

根据式(29)(30)结合矩阵卡尔曼滤波基本方程就可以搭建矩阵卡尔曼滤波器实现对初始姿态对应的K矩阵进行估计，完整估计过程如下：

卡尔曼滤波的初始化：

量测更新：

2.3 量测方差阵的推导

式(32)可等价于

其中，

对式(44)进行向量化处理，得：

其中163×矩阵M为

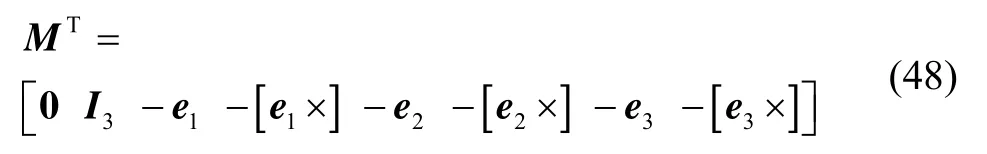
对式(47)两边求转置，得：

将式(49)代入式(46)得：

定义16×16矩阵Λi如下：

即式(50)可写为：

将式(52)代入式(43)得：

由于δbi为零均值白噪声过程的线性组合，所以均值也为零，方差的计算如下：

3 试验验证

为验证文中惯性系矩阵卡尔曼滤波算法的有效性，利用某型激光捷联惯组在车载晃动基座下进行四方位自对准试验，其中激光陀螺的零偏稳定性为0.01 (°)/h，随机游走系数为0.003 (°)/h1/2，石英挠性加速度计的零偏稳定性为100 μg，随机游走系数为100 μg/Hz1/2。试验时将惯组固联在车厢中部的底板上，在每个位置方位下重复对准六次，对准时间5 min，每次对准试验均对系统进行重启。对准期间，开启发动机怠速，并通过试验人员上下、开关车门、故意摇晃等方式施加干扰。

考虑试验车上无法获取载体真实的航向基准，为了评估算法的有效性，这里采用在同一方位下进行多次对准，以多次对准结果的标准差的方法间接进行评估[8]。同时将文中的方法同传统的“惯性系粗对准+导航系精对准”的线性卡尔曼滤波方法进行对比，进一步验证了设计的惯性系MKF算法的有效性。

图2 激光惯组在车厢内的安装位置Fig.2 IMU mounting position on experimental platform

图3～6分别给出了四方位下，MKF算法的重复对准试验方位角估计收敛曲线。表1则给出了各组对准结束时刻，惯性系MKF算法和传统KF算法的方位角估计均值和统计结果。

根据图3～6的MKF算法方位估计收敛曲线可知，文中所设计的惯性系 MKF算法的优点在于无需姿态初值，即可实现任意姿态条件下的快速自对准，不存在传统KF方法参数设置随机性而影响状态的估计速度问题，且收敛速度与载体姿态无关。

对比表1中方位对准的统计结果，就滤波收敛精度而言，惯性系 MKF算法对准结果的统计特性略优于传统KF算法，统计方位均方差小于3(1)σ′。

图3 方位1时航向角估计结果Fig.3 Estimation of yaw at Ori.1

图4 方位2时航向角估计结果Fig.4 Estimation of yaw at Ori.2

图5 方位3时航向角估计结果Fig.5 Estimation of yaw at Ori.3

图6 方位4时航向角估计结果Fig.6 Estimation of yaw at Ori.4

图7 方位1时MKF和REQUEST对准统计结果对比Fig.7 Means and ±3σ envelopes of yaw at Ori.1

就滤波模型而言，文中设计的 MKF对准算法，状态空间模型简单且无模型误差，而且滤波过程不必进行时间更新，仅保留了卡尔曼滤波的量测更新过程，收敛曲线非常光滑。

此外，为了对比MKF与传统REQUEST算法，图7给出了在方位1时的对准统计结果对比。其中实线表示均值，虚线表示方差。从图中可看出，MKF比传统REQUEST收敛速度略快，也更平稳。

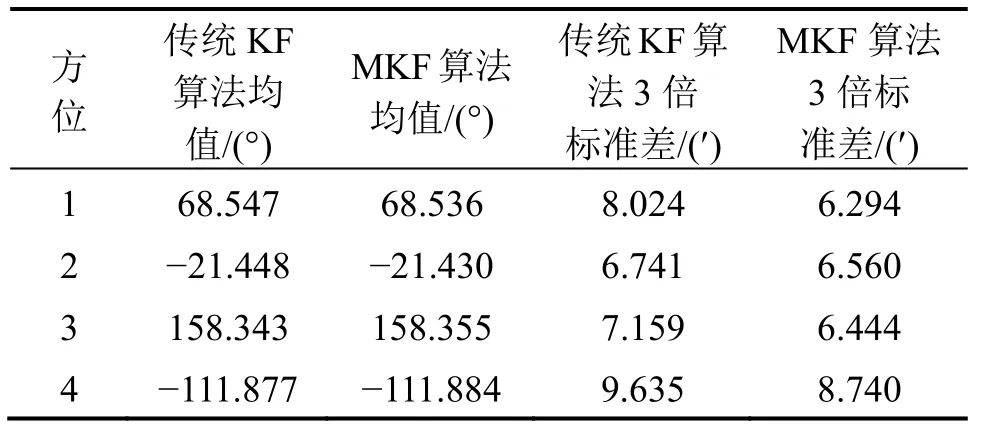
表1 对准结束时刻方位角结果对比Tab.1 Comparison of the final estimated yaw angles

4 结 论

针对晃动基座任意失准角下的快速自对准，文中提出了以重力加速度在惯性空间积分矢量作为观测量测的矩阵卡尔曼滤波初始对准算法。该方法利用重力矢量在惯性空间旋转成圆锥的特性并利用初始姿态为常值的特点，巧妙地推导了基于初始姿态K矩阵的矩阵卡尔曼滤波对准算法。该算法不必进行时间更新，可有效减少计算量，适用于任意姿态初值且无需进行粗对准，可在摆动状态下实现初始对准且可达到惯导系统对准的极限精度，具有很好的工程实用价值。