高铁再生制动工况下公用电网负序电流优化

罗 培，杨维民，张 敏

(湘潭大学 信息工程学院，湖南 湘潭 411105)

近年来，中国的高速铁路有了快速发展,我国已成为世界上高速铁路运营最快、里程最长的国家。高速铁路因电力机车负载不平衡产生的负序电流问题却日益严重。负序电流能够引起电力系统发电机转子过热、振动，引起继电保护装置误动作等一系列问题，给公用电网和列车的安全稳定运行带来隐患[1]。为减少负序电流对电气化铁路的影响，国内外学者提出了一系列补偿装置[2-3]，其中较为典型的为采取静止无功补偿器(Static Var Compensator, SVC)[4]、静止无功发生器(Static Var Generator, SVG)[5]、铁路功率调节器(Railway Power Controller, RPC)[6]等方法。由于能平衡2个供电臂之间的有功功率，采用RPC在治理负序电流问题表现出良好的应用前景。

文献[7]着重分析了负序电流产生机理，并对牵引工况下负序电流给出了计算和分析，文献[8]提出基于潮流控制器(Power Flow Controller,PFC)的补偿方法，能有效抑制负序电流，但这些研究并未考虑列车制动情况下的补偿，实际上高速交流传动电力机车在制动过程中会产生很大的再生制动能量[9-10]。目前高速铁路产生的再生制动能量主要包含2种利用途径：第1种是通过功率转移到另一供电臂被正在牵引运行的高速列车所吸收；第2种是直接通过牵引变压器反馈给公用电网，这种方法将增加公用电网的负序电流，在反馈的再生制动能量较大时可能对公用电网中的其他设备产生影响。目前没有关于高速铁路牵引供电系统在再生制动工况下的负序电流补偿相关文献。

超级电容(Super Capacitor, SC)具有快速充放电、低污染、高效率等特点而广泛应用于城轨列车系统和地铁系统[11]，为解决高速列车再生制动工况产生巨大能量流入公用电网造成负序电流急剧增加的问题，本文提出一种基于SC储能的铁路功率调节器(SC-RPC)，通过分析SC-RPC牵引工况和再生制动工况的电气模型，推导出公用电网负序电流的表达式，并提出SC-RPC的约束条件，采用改进粒子群算法求解，以负序电流最小为目标函数，各项指标为约束，求解全局最优解。最后提出相应的控制策略，通过仿真实验验证了该方法的有效性。

1 SC-RPC结构

SC-RPC的结构如图1所示。图中：IA，IB，IC为变压器一次侧电流；UA，UB，UC为变压器一次侧电压；Ia和Ib为变压器二次侧a，b供电臂电流；Iac和Ibc为a,b供电臂补偿电流；IaL和IbL为a，b供电臂负载电流；Is为SC电流。

图1 SC-RPC结构

由图1可知，该系统包括V/v变压器、RPC和SC，其中RPC由降压变压器T1和T2、单相电压源换流器VSC1和VSC2、直流电容C及串联电抗器L1和L2组成。SC主要采用双向DC/DC变换器将产生的再生制动能量储存到超级电容中，防止制动能量通过变压器流向公用电网，从而降低公用电网的负序电流。

2 SC-RPC电气模型

2.1 牵引工况下

牵引工况下SC-RPC单侧供电臂的电气模型如图2所示。图中：Ua为a供电臂电压；Ra为a供电臂V/v变压器等效电阻；La为V/v变压器等效电感；RL为负载等效电阻；L为负载的等效电感；IaLp为a供电臂负载的有功电流；IaLq为a供电臂负载的无功电流；Iacp为a供电臂SC-RPC的补偿有功电流；Iacq为a供电臂SC-RPC的补偿无功电流。

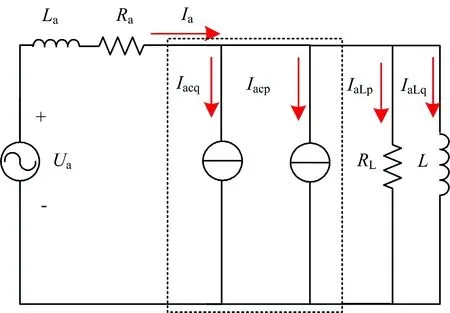
图2 牵引工况下SC-RPC单侧供电臂的电气模型

牵引工况下SC不工作，RPC通过有功功率和无功功率补偿对供电电网进行补偿。关于牵引工况下RPC的补偿，有大量文献提出了很多方法，本文不再赘述。

2.2 再生制动工况下

再生制动工况下SC-RPC单侧供电臂的电气模型如图3所示。再生制动工况下，列车制动产生再生制动能量，方向为从供电臂流向公用电网，此时SC工作。再生制动工况下，产生的再生制动能量若不能被转移或存储，就会流入公用电网，可能对公用电网中的其他设备产生影响。

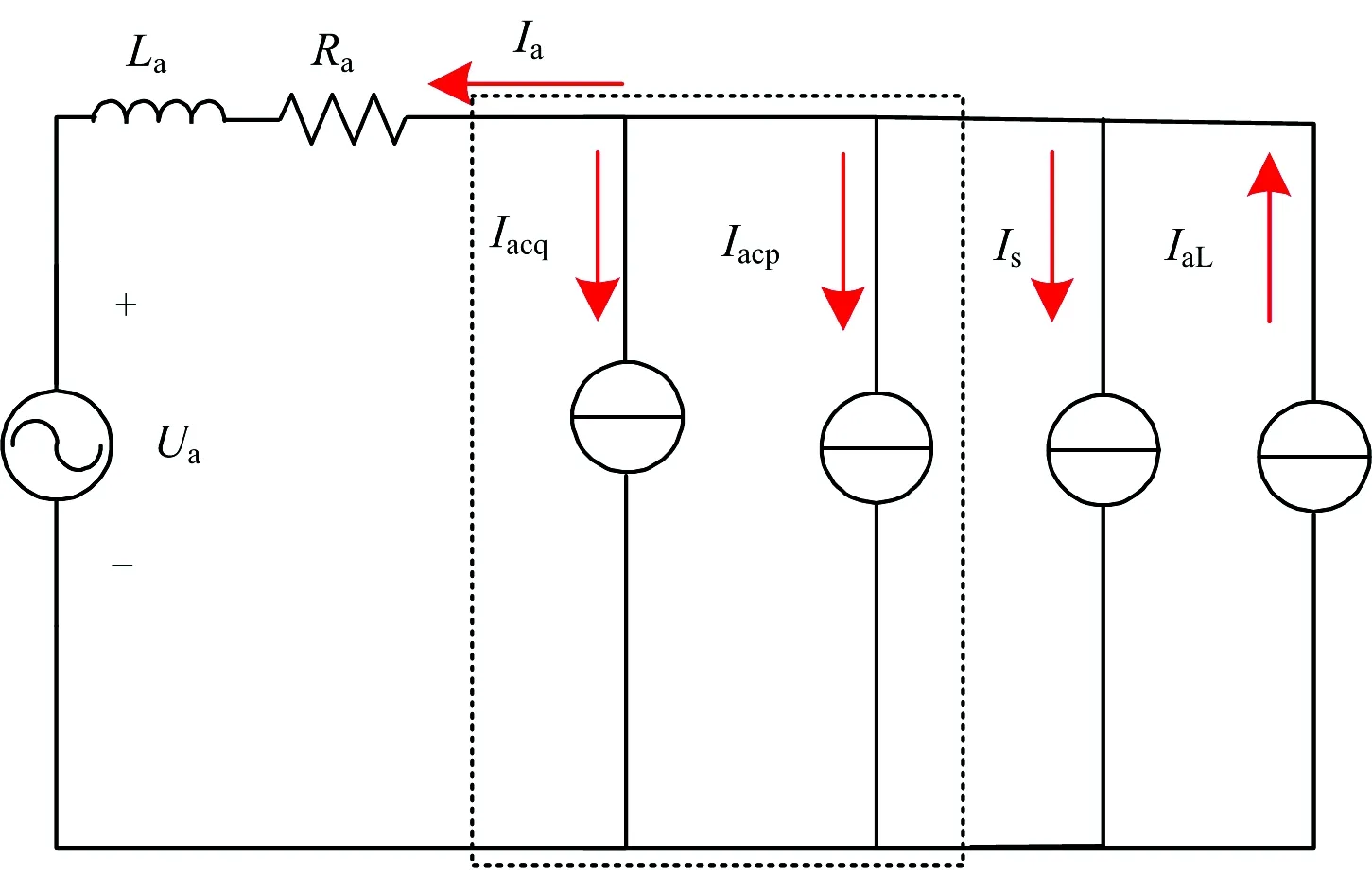
图3 再生制动工况下SC-RPC单侧供电臂的电气模型

3 SC-RPC再生制动工况下最小负序电流数学模型

3.1 负序电流的表达式

SC-RPC再生制动工况下的向量图如图4所示。图中：θa，θb分别为a，b这2个电臂的功率因数角；Ub为b供电臂电压。a供电臂为牵引工况，电流IaL位于第四象限，b供电臂为再生制动工况，电流IbL位于第二象限。θb>π/2，表示b供电臂为再生制动工况，处于放电状态。

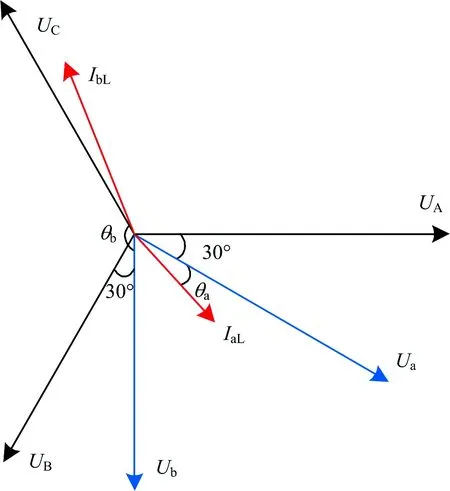
图4 再生制动工况下的向量图

补偿前，公用电网的负序电流I-[7]较大，为

(1)

式中：K为变压器匝数比。

由于并联了SC，Ia，Ib，θa，θb和Is之间的关系为

(2)

式中：IbLp为b供电臂负载的有功电流；IbLq为b供电臂负载的无功电流；Ibcp为b供电臂SC-RPC的补偿有功电流；Ibcq为b供电臂的补偿无功电流。

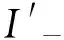
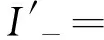
(IbLp-Ibcp-Is)2+(IbLq-Iacq)2+

(3)

3.2 约束条件

1)SC-RPC有功功率传输平衡限制

忽略损耗即SC-RPC不消耗有功功率，SC-RPC补偿前后的有功功率是相等的。RPC补偿的有功电流为ΔI，方向从b供电臂到a供电臂，则SC-RPC有功功率传输平衡限制为

ΔI=Iacp=-Ibcp

(4)

2)超级电容最大电流限制

(5)

3) 2个供电臂电压波动范围限制

牵引变压器和牵引网线路的阻抗较大，列车负载的波动也非常大，所以牵引网电压的过压、欠压对列车会产生不利影响。2个供电臂电压波动范围限制为

(6)

式中：Umax+为最大电压的波动上限；Umax-为最大电压的波动下限；ω为角频率；Rb为b供电臂V/v变压器等效电阻。

4)公用电网功率因数限制

根据国家标准，要求在牵引网高压计量点处的三相电网功率因数pf不小于0.9，则公用电网功率因数限制为

Pf=[Ua(IaLp+Iacp)+Ub(IbLp-Ibcp-Is)]/{[Ua(IaLp+Iacp)+Ub(IbLp-Ibcp-Is)]2+[Ua(IaLq+Iacq)+

(7)

5)设备电流限制

由于电流限制，SC-RPC中Iacp和Ibcq的瞬时值都不能超过其限制值。假设SC-RPC最大电流为Icmax,最大传输有功功率为Pmax，则设备电流限制为

(8)

6)变压器容量限制

由于变压器容量的限制，a，b供电臂补偿后的瞬时功率不能比单个线圈的额定功率大，则变压器容量限制为

(9)

式中：Pa为变压器额定功率。

3.3 SC-RPC负序电流优化数学模型

综上可知，再生制动工况下的负序电流优化是1个多维、非线性约束的优化问题。SC-RPC补偿后公用电网最小负序电流数学模型的目标函数为式(3)，约束条件为式(4)—式(9)。式(3)中，IaLp，IaLq，Iacp，Iacq为可测量参数，则该目标函数的决策向量为由ΔI，Iacq，Ibcq，Is组成的4维向量，即目标函数的求解由1个等式、10个不等式约束。

4 改进粒子群算法求解数学模型

目前求解多维非线性问题有很多，如模拟退火算法、遗传算法、蚁群算法等。粒子群算法由于寻优能力强、收敛速度快等优点，在电力系统获得越来越多的关注[12]。本文采用粒子群算法求解公用电网负序电流优化问题。

4.1 改进粒子群算法

粒子群算法中，粒子的全局搜索能力和当前的惯性权重取值密切相关，用wi(t)表示，取值的好坏，影响着算法的收敛性。常用的惯性权重取值是随着迭代次数的递增线性递增或者递减，该方法对惯性权重的取值缺乏指导。本文利用粒子与种群全局最优解的距离指导权重取值。

wi(t)=wmax-(wmax-wmin)(di(t)-1)2

(10)

其中,

式中：wi(t)为t时刻第i个粒子的权重；wmin和wmax分别为w的最小值和最大值；di(t)为t时刻第i个粒子与种群全局最优解的距离；xmax和xmin分别为粒子位置的最大值和最小值；D为解空间维数；xgj(t)为当前粒子t时刻全局最优解；xij(t)为粒子t时刻位置。

当粒子与全局最优值距离较大时，权重w取值较大，粒子全局搜索能力增强，当粒子与全局最优值距离较小时，权重w取值较小，提高了粒子局部搜索能力。

4.2 改进粒子群算法求解

改进粒子群算法求解最小负序电流数学模型时的具体流程图如图5所示。

5 SC-RPC再生制动工况下控制策略

5.1 SC-RPC控制结构

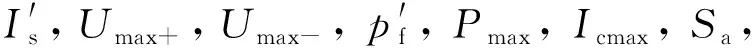
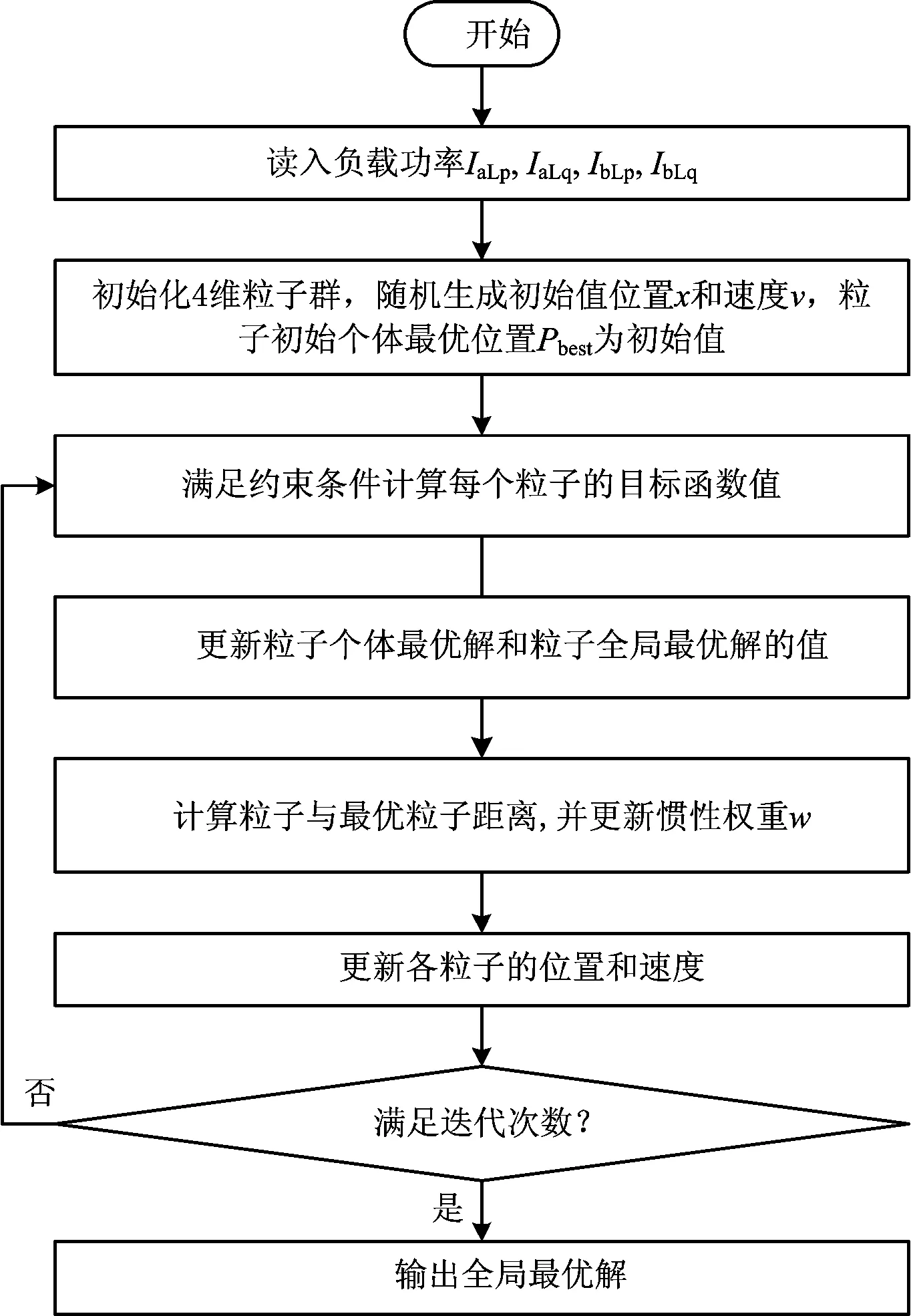
图5 改进粒子群算法求解模型流程图

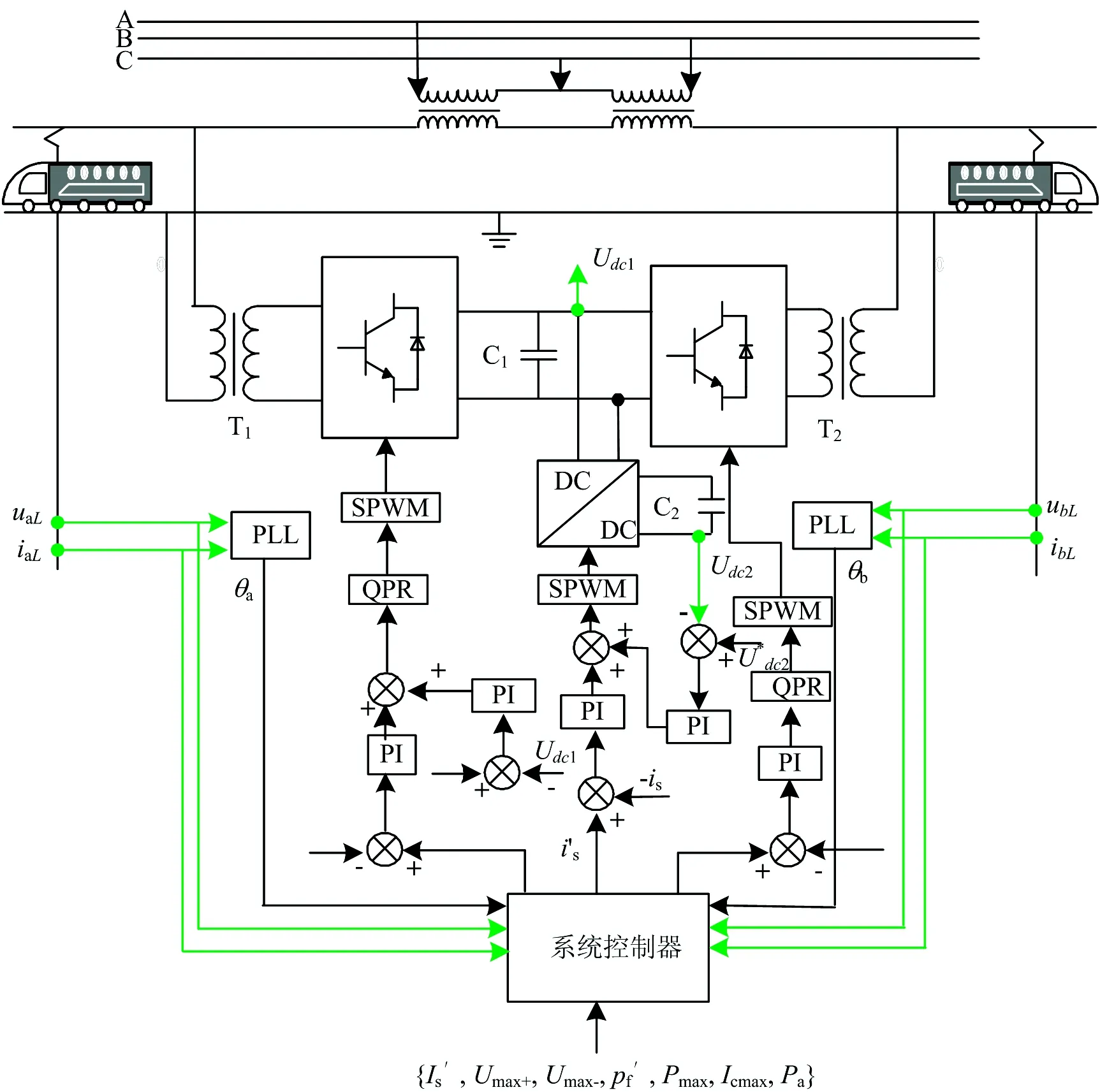
图6 SC-RPC控制系统结构图

5.2 RPC控制策略

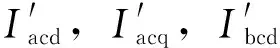
5.3 SC控制策略

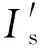
6 仿真验证

为了验证再生制动工况下SC-RPC负序电流优化方案的有效性，搭建Matlab仿真系统，参数见表1。

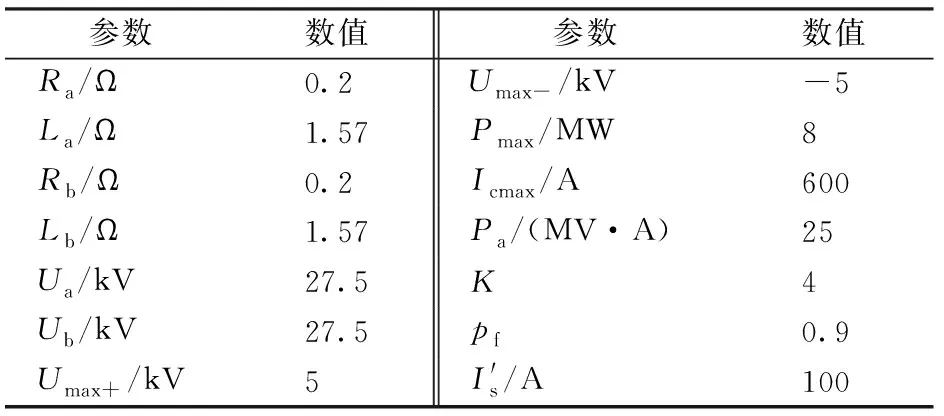
表1 牵引供电系统仿真参数

6.1 不同再生制动工况下的补偿结果

为检验不同再生制动工况下本文方法的有效性，设置5种不同工况进行试验。SC最大电流限制、2个供电臂电压波动、功率因数、设备容量、变压器最大容量见表2，最小负序电流优化补偿效果见表2。

表2 优化补偿效果

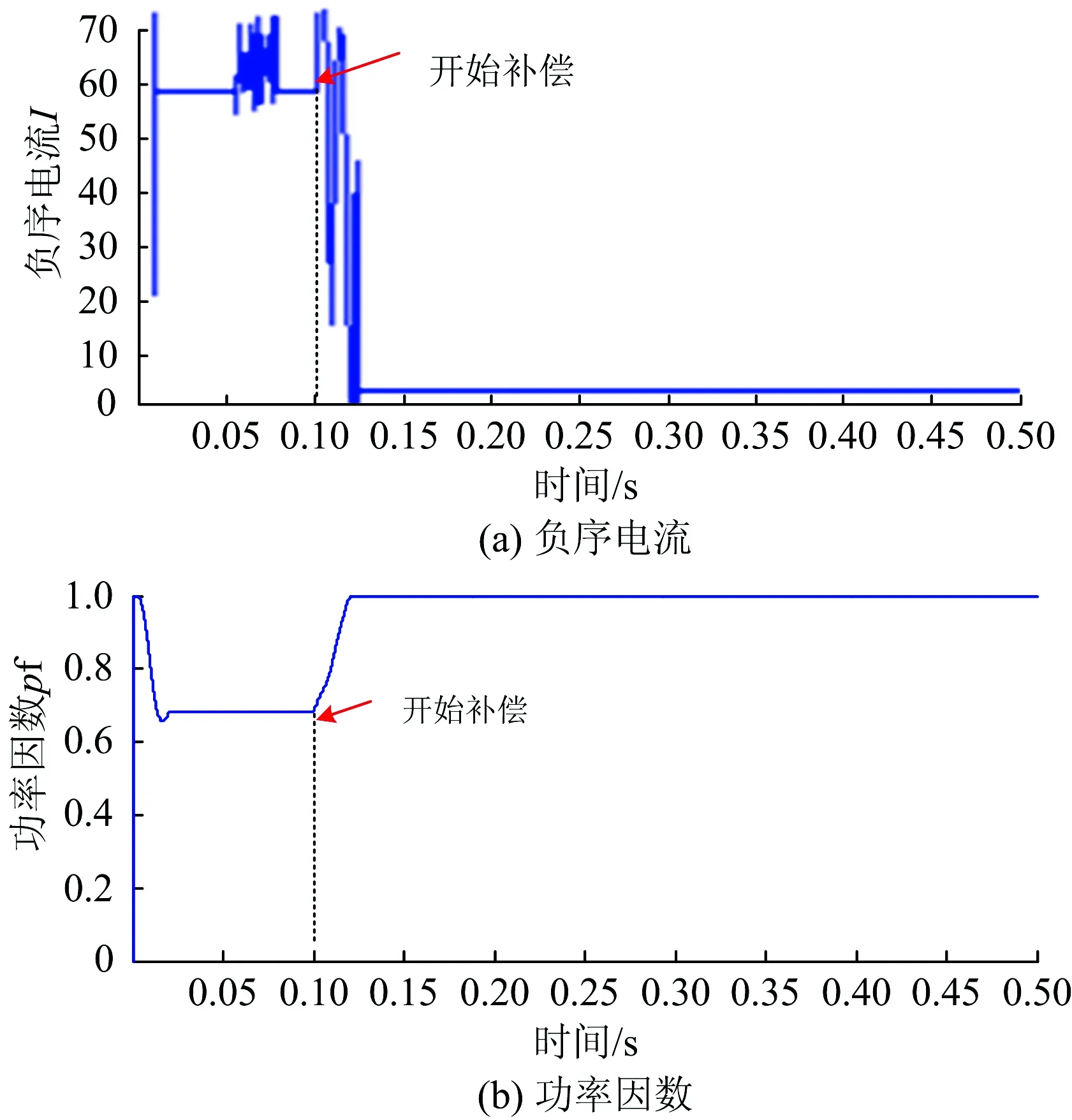
由表3可见：工况1下a供电臂中的再生制动能量一部分流向b供电臂，一部分被存储在超级电容中，转移的有功电流为122 A，超级电容的指令值最优值为68 A，补偿后负序电流降低约92%，抑制效果明显；工况2下-IaLp

6.2 补偿结果的仿真验证

为检验本文方法在有效降低负序电流的同时功率因数是否达标，对照图1，利用Matlab构建仿真系统。仿真时间为0.5 s，在0.1 s采用SC-RPC进行补偿。假设a供电臂为再生制动状态，b供电臂为正常牵引状态，IaLp=-150 A,IaLq=30 A,IbLp=130 A,IbLq=50 A。利用SC-RPC进行补偿时，控制策略采用上文所述方法。

优化补偿效果的仿真结果如图7所示。由图7可见：补偿前负序电流为60.2A，补偿后负序电流降低至4.3 A，降低约92%；与此同时，补偿后功率因数达到电能质量要求(pf≥0.9)；仿真结果验证了本文所提方法的有效性。

图7 优化补偿效果

7 结 语

通过建立SC-RPC再生制动工况的电气模型，分析补偿原理，构建了SC-RPC的最小负序电流数学模型，采用粒子群算法，通过自适应调整粒子的惯性权重，快速求解全局最优解，并提出相应的控制策略，最后通过仿真实验验证了该方法在再生制动工况下抑制公用电网负序电流的有效性。