航天器结构声振耦合问题的有限元-边界元方法数值仿真研究
冯金龙,王宏宏,赵营,王一楠,杜骊刚
(北京机电工程总体设计部,北京 100854)
声振耦合环境是航天器飞行过程中遇到的主要动力学环境之一,尤其是高超声速飞行器,声振耦合环境更加恶劣,精准的动力学环境预示越发困难,但更迫切。声振耦合环境其主要效应是激起航天器主次结构共振响应以及局部动力响应过大,造成结构破坏、局部失稳、电子元器件等敏感组件发生故障。如何准确地预示在外声场作用下飞行器的内声场以及由此引起的其结构上的振动响应,对于航天器上的仪器设备、结构本身以及有效载荷具有十分重要的意义[1]。
结构轻量化的要求使得薄壁结构和轻质材料得到了广泛的采用。随着结构越来越薄,声振耦合响应变得越来越剧烈。新型材料的应用,增加了声振耦合问题研究的难度。与此同时,航天器正在向功能多样化,结构复杂化发展。这些都给声振耦合问题的研究带来了新的挑战。
随着计算机技术的发展,结构精细化建模水平的提高,数值计算理论的进步,计算机数值仿真技术得到了广泛的应用,在解决实际工程中,发挥了越来越大的作用。因此,结合我国高超声速航天器研制需要,开展航天器声振耦合问题数值仿真方法研究,对提高航天器动力学环境预示精度、减轻结构质量、降低分系统设计难度具有重要工程意义。
1 声振耦合问题的数值仿真方法
航天器声振耦合问题是全频域问题,包括低频段、中频段和高频段。低频段的声振耦合响应呈现确定性特性,高频段的声振耦合响应呈现统计性特性,中频段声振耦合响应特性介于确定性和统计性之间。因此,不能用同一种数值仿真方法求解全频段的声振耦合问题。
随着科学理论的不断发展,各种数值仿真方法不断涌现,并投入实际工程设计中。在航天领域,用于求解声振耦合问题的方法主要有:有限元法(FEM)、有限元-边界元(FEM-BEM)方法、有限元-统计能量法(FEM-SEA)、统计能量法(SEA)等。
FEM 法最早应用于航天器结构强度分析和动力学分析[2]。在低频段,可以将声场假设成动力学载荷,通过有限元的频响分析方法,求解结构的声振耦合响应。这里要求声场是确定的、低频的,因此,FEM法是确定性方法。另一方面,当声场处于内声场时,也可以用声学有限元方法进行求解。声场和结构都采用有限元方法,耦合效果很好。
20世纪90年代Everstine和Henderson提出了第一个求解声振耦合问题的FEM-BEM算法,从此开启了FEM-BEM方法求解声振耦合问题的研究[3]。该方法用有限元法求解结构的动态响应,用边界元法模拟外部声场,利用边界条件,实现声场与结构的耦合。充分发挥了有限元法进行结构分析的优点和边界元法求解声学问题的优势,是一种求解声振耦合问题的有效计算方法[4]。FEM-BEM方法在国内外航天领域,尤其是卫星、天线、太阳帆板等声振耦合分析、动力学环境预示方面应用非常广泛,并取得了良好的效果[5-6]。大量的工程案例表明,FEM-BEM 方法是进行航天器低中频声振耦合问题分析的有效数值仿真方法[7-8]。
19世纪60年代,R. H. Lyon 提出了统计能量分析方法(SEA)。统计能量分析的基本出发点是将一个完整的系统根据存储能量的方式离散成 N个子系统,在外界激励源作用下,各个子系统间进行能量交换,确定了每个子系统存储的能量后,便可计算出各个子系统的的振动参数如位移、速度、加速度、声压等。应用 SEA进行航天器声振耦合分析时,强调的是“统计”模型,在结构分析、参数确定以及响应计算等过程中,无不渗透着“统计”的概念,这也正是其能够应用于航天器研制初期阶段以及高频范围环境预示的根本原因[9]。因此,SEA方法特别适用于型号结构形状与尺寸尚未确定的研制初期阶段的高频段声振耦合分析。
FEM-SEA方法是一种基于波动理论的数值仿真方法。该方法首先将系统进行划分:波长大于特征尺寸的子系统,划分为确定性子系统,采用FEM建模;波长小于特征尺寸的子系统,划分为随机子系统,采用 SEA建模。确定性子系统和随机子系统由连接边界上的直接场和混响场的互易关系耦合,然后求解得到整体系统的响应[10]。
航天器在低中频段内的声振耦合响应,对航天器动力学特性具有重要意义。因此,本文主要围绕求解低中频声振耦合问题的FEM-BEM方法开展研究,包括FEM-BEM方法的基本原理、数值仿真过程及地面试验验证技术研究。
2 FEM-BEM耦合方法理论
2.1 声学问题的Burton-Miller边界元方程
为了简便,直接给出声学问题的 Burton-Miller边界积分方程为:
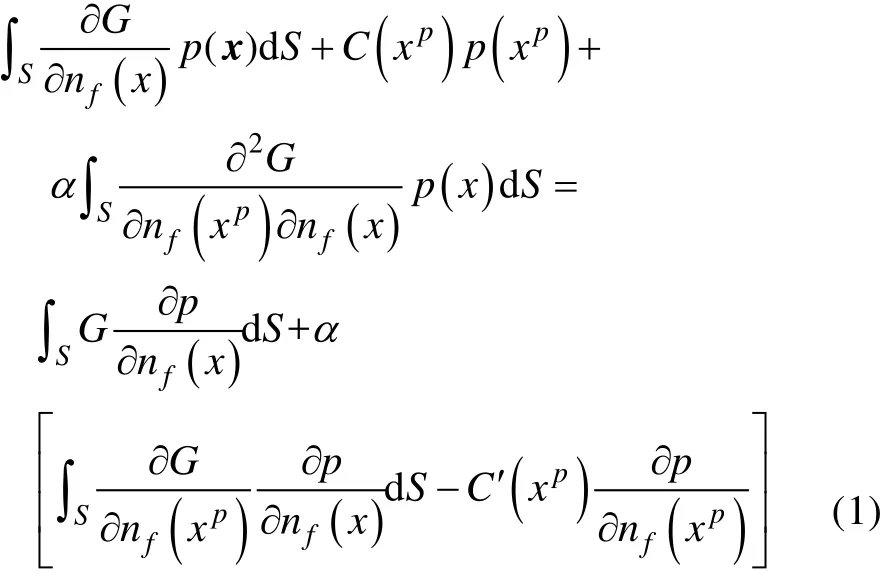
式中: xp为源点;x为场点;为基本解; p( x)为点x处的声压;为入射波产生的声压; nf(x)为边界S上x点的外法线方向,指向流体的外侧; ρf为流体的密度; vn(x)为法向速度;α为组合系数;为自由项系数。
方程(1)可以表示成矩阵形式:

2.2 结构动力学有限元方法
整个系统的动力学有限元方程可写为:
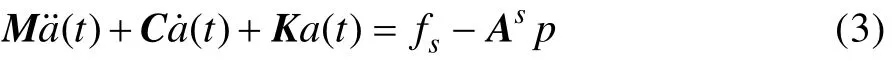
式中:M为系统质量矩阵;C为阻尼矩阵;K为刚度矩阵; fs为体力向量;sA为转换矩阵;p为表面声压。
在不考虑体力的情况下,则运动方程为:

设动力学方程的解具有如下形式:

将式(4)转化到频率域中得到:
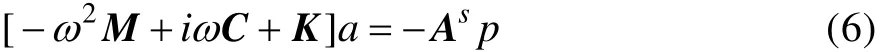
又因为质点速度与位移有以下关系:

把式(7)代入式(6)中得到:
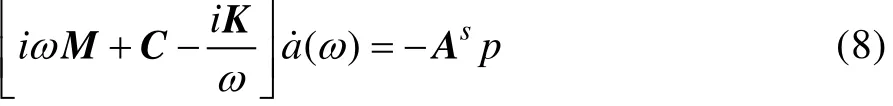
通过方程(8)可以得到计算辐射声压所需的表面法向速度。
2.3 BEM/FEM耦合方法
将方程(2)和方程(8)联立,即可求出频率域内的质点速度和声压。
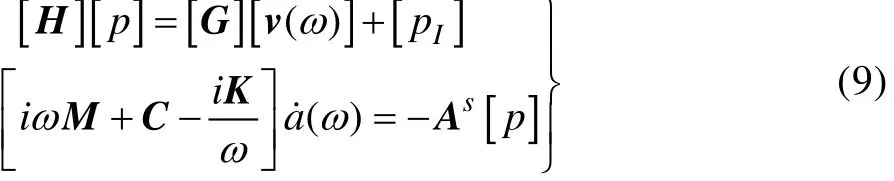
由方程(9)的第二式可得:
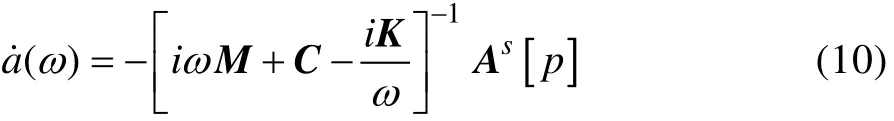

将式(11)带入式(9)的第一式,得到:
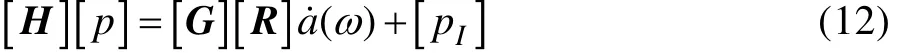
将式(10)带入式(12)中可得:
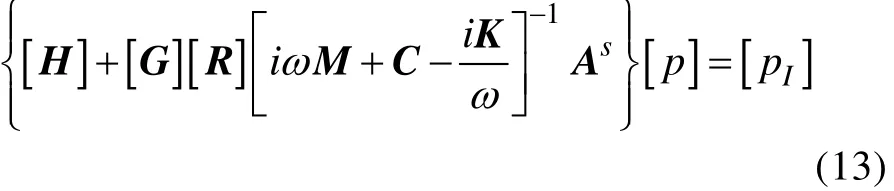
求式(13),可以得到表面各点的声压。
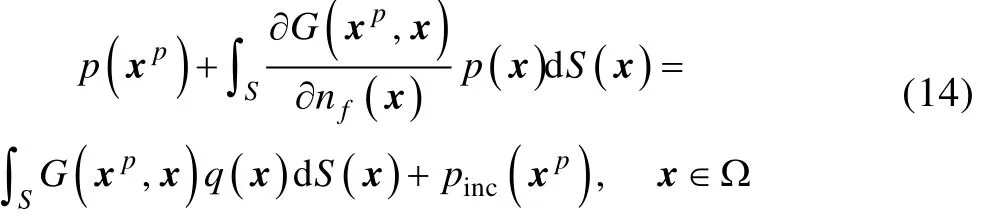
通过式(14)可以获得域内任意点的声压值。
3 数值仿真及结构分析
在掌握FEM-BEM方法基本理论的基础上,以航天器典型结构为研究对象,开展声振耦合问题的仿真分析应用研究。该算例涉及到了FEM-BEM方法在应用过程中基础操作流程,为该方法的应用提供了基础。
3.1 几何及材料信息
选取结构长1.0 m,前后端不封闭,前后端半径分别为0.8 m和0.5 m,结构壁厚为0.004 m,结构内筋尺寸为0.004 m×0.008 m。材料弹性模量200 GPa,泊松比0.3。结构部含有若干设备。
3.2 结构模态分析
声振耦合分析的第一步就是建立结构的动力学模型,并进行结构模态求解。采用MSC.Patran 2014进行建模,求解频率范围2000 Hz以内。结构蒙皮采用4节点壳单元,结构内筋采用2节点梁单元。在模态分析中,结构内直接挂壁安装在结构壁上的设备,采用了0D的质量单元代替,通过RBE2单元将其连接。结构内主要支撑结构,采用壳单元模拟或梁单元模拟,通过RBE2单元连接在结构壁上。有限元模型如图1所示。
模态求解计算采用有限元软件MSC.MD Nastran 2011.1,计算结果输出文件格式为.Op2。该文件作为声振耦合分析的有限元系统模型文件。结构的前四阶固有频率分别为:75.8、149.5、164.2、179.8 Hz,对应的振型如图2所示。
从图2可以看出,结构的一阶振型以结构内大梁变形为主,二阶振型和三阶振型以结构前端呼吸模态为主,四阶振型以中部呼吸模态为主。结构模态比较复杂,内部设备及支撑对整体结构的动力学特性影响显著。为了更清晰地分析结构的模态特性,将结构单独取出,进行模态分析。计算得到结构前三阶固有频率分别为85.1、123.5、278.2、345.6 Hz,振型如图3所示。

图1 结构有限元模型

图2 舱体前四阶振型
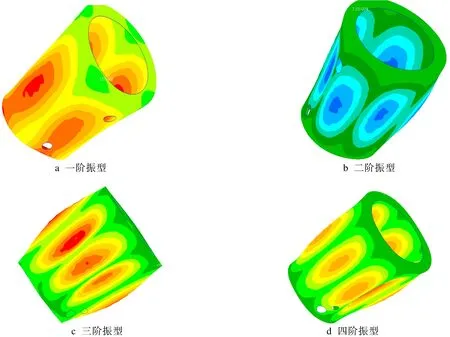
图3 结构前四阶振型
从图3可以看出,结构的模态振型以呼吸模态为主,且振型清晰规则。对比图2和图3,可以看出,结构内部设备的安装、支撑的布置改变了原来结构的振型,且变化很大。因此,有必要开展从单舱到舱内含设备各种状态的舱体模态试验,来校核修正有限元模型。数值仿真结果可以为试验方案的制定提供参考依据。
3.3 声振耦合模型
声振耦合模型的建立和求解采用软件 VA One 2015-64bit。声振耦合模型由结构有限元系统和边界元流体系统两部分组成。
首先,将结构模态分析结果文件.Op2中的信息导入声振耦合模型,作为耦合模型的结构有限元系统。该系统包含结构有限元模型和模态信息,同时会自动生成有限元模型的边界,作为边界元流体施加的区域。
其次,设置求解频率、分析带宽,建立边界元流体系统。根据有限元系统的模态分析结果,设置该耦合模型的求解频率范围40~1000 Hz,设置分析带宽为5 Hz等带宽,声压级为165 dB。为减少计算量,对自动生成的有限元模型的边界面进行重新划分网格,作为边界元流体的网格。声振耦合模型如图4所示。
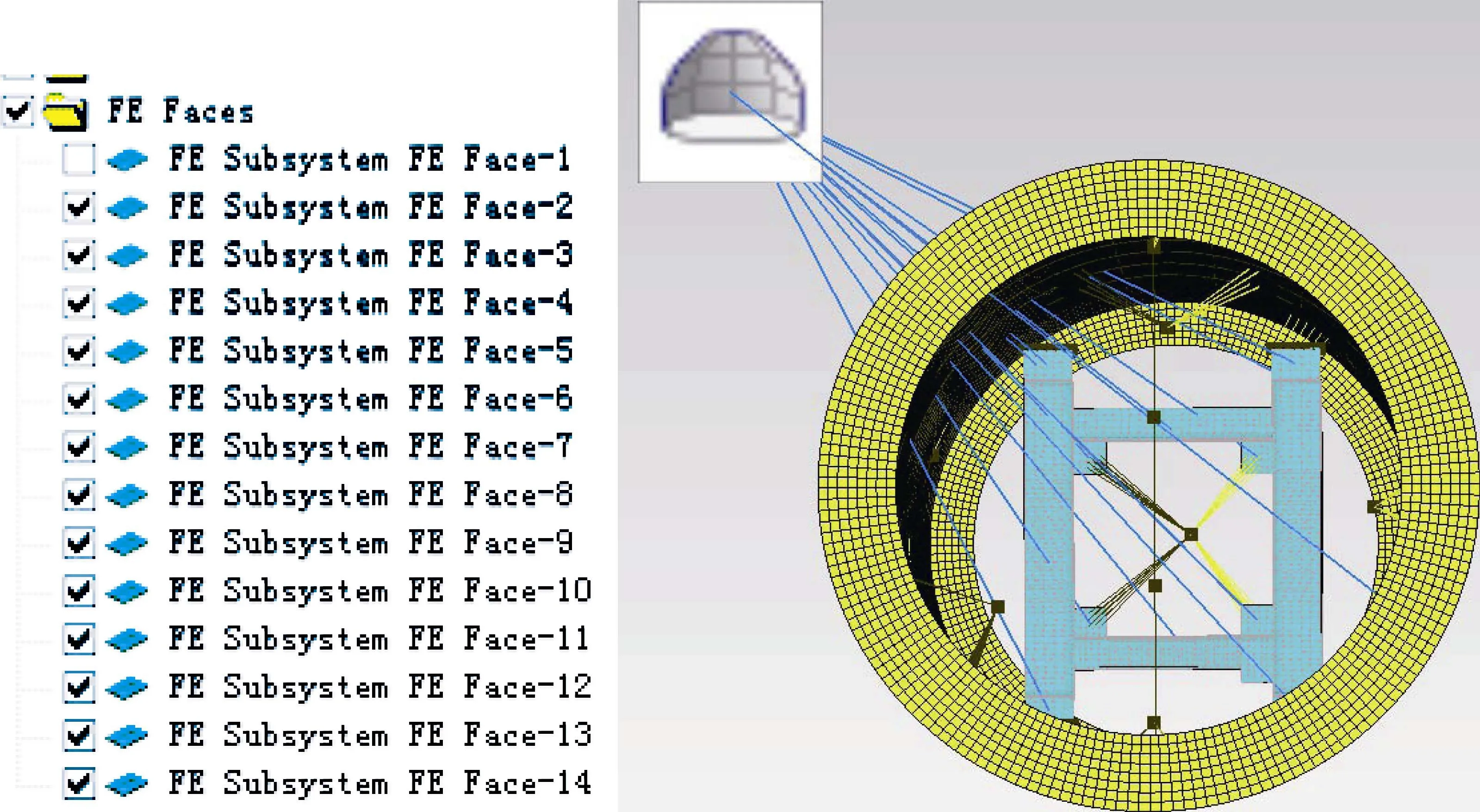
图4 声振耦合模型
为了获得不同区域的动态响应特性,在结构壁面不同位置、局部削弱处、筋条处、支撑上、支撑与舱壁连接处、集中质量单元上分别布置了振动传感器和传声器,如图5所示。
3.4 计算结果分析
用 FEM-BEM 方法对上述结构进行声振耦合数值仿真分析,可以获得结构的整体和局部动态响应、结构表面和局部任意位置的声压分布和结构的动应力响应。
通过计算,获得平均动态响应,如图6所示,可以作为结构动力学环境预示的功率谱密度图。
由于结构壁面特征不均匀,结构的 PSD谱是整个区域的动态响应的平均值。通过在结构表面均匀布置传感器,获得不同区域的,如图7所示。
结构上开孔处,是局部削弱区。在强度校核时,该区域应该是校核的重点,通过传感器给出这些区域的动态响应,给结构设计提供参考,如图8所示。
动力学环境预示最重要的就是给出结构内各设备安装处的动力学响应,通过声振耦合仿真分析,给出不同设备各个位置上的动态响应,将为系统级试验提供更准确的力学试验条件,如图9—11所示。
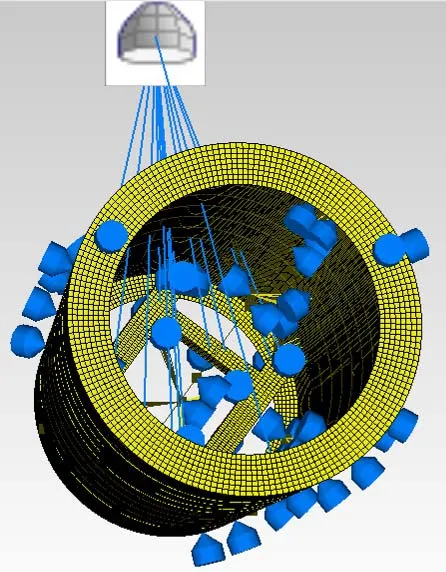
图5 传感器布置
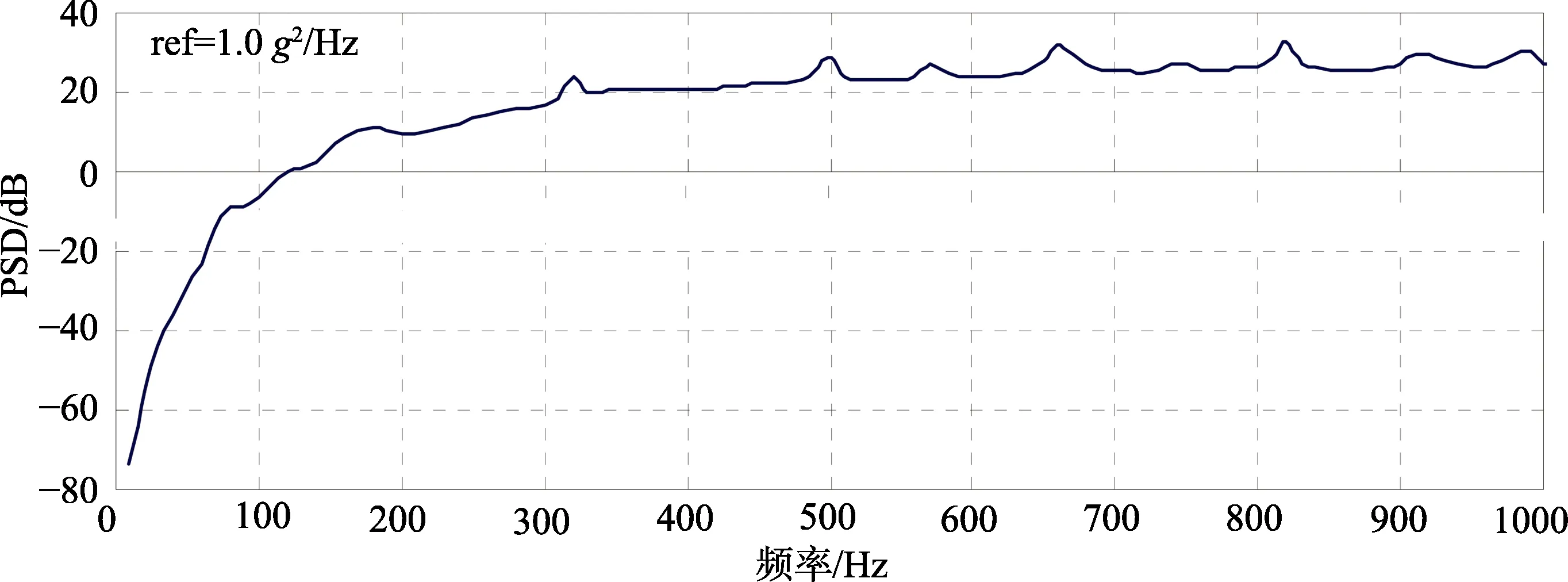
图6 结构平均动态响应
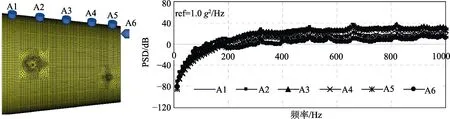
图7 结构表面的振动响应
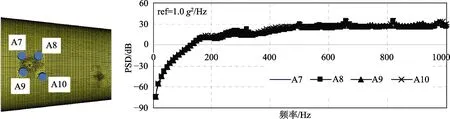
图8 局部开孔处的振动响应
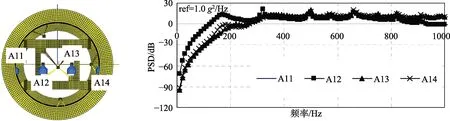
图9 大梁上振动响应
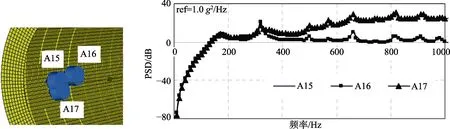
图10 大梁连接处动态响应

图11 不同设备上的动态响应
4 结语
文中针对航天器飞行过程中声振耦合响应难以精准预示的问题,研究了当前求解声振耦合仿真问题的各种数值方法,并给出了各种方法的适用范围。以求解低中频声振耦合问题的 FEM-BEM 方法为突破口,开展了该方法的理论研究、数值仿真方法研究。声振耦合模型包括结构有限元模型和声学边界元模型,涉及参数多、边界条件复杂,必须通过开展相应的模态试验和噪声试验,对数值仿真模型进行修正和校核。相关试验已经完成,正在进行试验数据整理。后续将撰写论文对地面试验验证技术及模型修正技术进行讨论。该研究内容为应用有限元-边界元方法研究航天器声振耦合问题提供了理论参考和数值仿真技术支持。

