频域子结构方法在力学环境预示中的应用研究
陈江攀,王冬,刘艺,刘艳,张为雯
(北京电子工程总体研究所,北京 100854)
随着科学技术的飞速发展,工程实际中的结构系统越来越复杂,利用FEM分析如飞行器、船舶以及车辆等大型复杂结构的动力学特性时,离散后的结构自由度往往是数以万计,甚至是数以十万、百万计,而所关心的往往只是复杂结构的少数低阶动力学特性,故采用直接法求解不仅受到计算机工作性能的限制,还大大降低计算效率,并提高计算成本[1]。动态子结构方法的提出与发展则有效地解决了这一问题,其基本思路是“先化整为零,再积零为整”[2]。该方法的优点为:1)整体结构的自由度得到大量缩减,从而在保证计算精度的基础上有效提升计算效率;2)可对所关注的子结构进行独立修改和优化,而其余子结构保持不变;3)大型复杂结构的各子结构可由不同部门在不同地区进行设计、测试和分析,然后再进行综合,即可获得整体耦合结构的动力学模型,便于分工协作;4)具有广泛的应用范围,可对分别基于有限元和试验测试所建立的子结构理论模型和试验模型进行综合[3]。
传统上按照求解域的不同可将动态子结构方法分为两类,即模态综合法(CMS,Component Mode Synthesis)和FBSM。CMS发展较早且方法较为成熟,并已得到了广泛的应用。该方法适用于基于有限元方法所建立的理论模型的综合问题,但工程实际中常存在由试验测试获得的试验模型以及理论-试验混合模型的综合问题。此时,则需基于子结构的频响函数矩阵进行处理[4-5],即FBSM。
最初的FBSM是阻抗耦合方法,阻抗耦合方法要求对子结构的全体自由度频响函数矩阵进行求逆,故计算精度和计算效率均较低,且当频响函数矩阵奇异时,该方法失效[6]。Jetmundsen等[7]在前人的研究基础上,发展了导纳耦合方法,导纳耦合方法只需对界面连接自由度的频响函数矩阵进行求逆,这使得该方法的计算精度和计算效率较阻抗耦合方法均大幅提高,但该方法仅适用于处理两个独立子结构之间的综合问题。在导纳耦合方法的基础上,Ren等[8]提出了一种适用范围更广的广义导纳耦合方法,该方法可直接用于处理多个非独立子结构之间的综合问题。值得指出的是,广义导纳耦合方法仅适用于处理子结构间为刚性连接的频域子结构综合问题,但工程结构中的连接大都为弹性连接[9]。为此,文献[10-12]基于广义导纳耦合方法,将子结构间的弹性连接划分成一个独立的连接子结构,对考虑弹性连接的FBSM进行了详细推导,形成了现有的考虑弹性连接的FBSM。
在上述研究成果的基础上,文中分别对处理子结构间为刚性连接和弹性连接两种问题的 FBSM 进行了理论推导,并通过设计算例仿真对FBSM的正确性进行了验证。此外,还就弹性连接的等效方法进行了讨论。
1 刚性连接FBSM推导
以图 1所示结构对处理子结构间为刚性连接问题的FBSM进行推导。
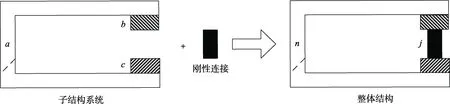
图1 刚性连接子结构系统及整体结构
图1中,a和n分别代表子结构系统和整体结构的内部结点自由度,b、c和j分别代表子结构系统和整体结构的界面结点自由度。此时,可将子结构系统和整体结构的频响函数矩分别写成如下形式:

式中:x、H和 f分别代表响应列向量、频响函数矩阵和激励列向量。引入位移协调和力平衡条件:

此外,由于综合前后,子结构系统和整体结构内部结点自由度的响应和激励均未发生变化,因此可得:

由式(1)和式(2)可得:

将式(2)和式(3)代入式(4)并整理可得:

此时,若矩阵(Hbb+Hcc-Hcb-Hbc)可逆,则式(5)可改写为:

将式(2)和式(6)代入式(1)并整理可得:
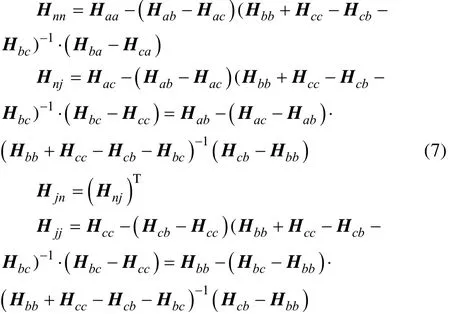
将式(7)写成矩阵形式如下:

式(8)即为处理子结构间为刚性连接问题的FBSM的表达式。其中,各子结构的频响函数矩阵可通过试验测试或理论计算获得。计算方法通常选用模态叠加法:

式中:mi、ci和 ki分别为子结构对应于第 i阶模态φi的模态质量、模态阻尼和模态刚度;j为虚数单位;ω为角频率;w为参加计算的模态总阶数,且由于w< 以图 2所示结构对处理子结构间为弹性连接问题的FBSM进行推导。 图2中:a代表内部结点自由度;b和c代表界面结点自由度;上标“-”和“~”分别代表子结构系统和弹性连接。此时,可将子结构系统的频响函数矩阵以及弹性连接的阻抗矩阵分别写为: 式中:Z代表阻抗矩阵。引入位移协调和力平衡条件为: 此外,由于综合前后,子结构系统和整体结构内部结点自由度的响应和激励均未发生变化,因此可得: 图2 弹性连接子结构系统及整体结构 由式(10)和式(11)可得: 由式(10)、式(11)和式(12)可得: 将式(14)代入式(13)并整理可得: 将式(15)写成矩阵的形式为: 式(16)中,若待求逆矩阵具有奇异性,可采用奇异值分解方法对其进行处理[13]。此时,将式(11)、式(12)以及式(16)代入式(10)并整理可得: 式(17)即为处理子结构间为弹性连接问题的FBSM的表达式。值得指出的是,式(17)中参与求逆的矩阵阶数仅为界面结点自由度数,故可显著提高计算效率。同理,式(17)中各子结构的频响函数矩阵也可通过试验测试或由式(9)所示的模态叠加法计算获得。 在利用式(17)对具有弹性连接的结构进行力学环境预示时,如何对弹性连接进行准确地等效将直接影响预示精度。文献[5, 14]利用6自由度标量弹簧-阻尼系统等效结构中的弹性连接,对具有弹性连接结构的力学环境预示方法进行了初步研究,并取得了一定的研究成果,但这种等效方法没有考虑弹性连接各自由度间的刚度耦合作用,与工程实际并不相符。由文献[15]可知,空间梁单元的刚度矩阵Kb的表达式为: 式中:A、E和G分别为空间梁单元的截面面积、 弹性模量和剪切模量;L为单元长度;Ix为单元截面的极惯性矩;Iy和Iz则分别表示单元截面对坐标轴y和z的惯性矩。 由式(18)可知,空间梁单元的结点刚度矩阵为非对角阵,存在垂向平动和弯曲的耦合项,故与六自由度标量弹簧相比,可更为准确地等效复杂结构中的弹性连接刚度。此外,弹性连接的质量远小于整体结构质量,对整体结构力学特性的影响可忽略不计[4,8]。此时,假设弹性连接为瑞利比例阻尼,则可将弹性连接的阻抗矩阵Z写为: 式中:β为比例阻尼系数。 为了验证上述推导所得分别处理子结构间为刚性连接和弹性连接两种问题的FBSM的正确性,设计了如图3所示的算例结构。图3中,P和Q为两根相同的矩形截面长梁,截面尺寸和梁长度分别为0.02 m× 0.04 m和0.5 m。C为弹性连接,采用两根相同的圆形截面短梁来等效,截面直径和梁长度分别为0.005 m和0.05 m。此外,P、Q和C均为瑞利比例阻尼。利用空间梁单元对弹性连接进行等效,并对P、Q和C进行单元划分,在此基础上,分别建立P、Q、C以及整体结构的有限元模型,单元属性见表1。 在上述基础上,分别利用FBSM和FEM对图3所示算例结构中结点1和结点2两个结点之间三个平动方向的频响函数进行计算,并将两种方法对应的计算结果进行了对比,如图4所示。其中,图3a所示子结构间为刚性连接的算例结构,其结点1和结点2两个结点之间的X-X平动方向在1000 Hz内无固有频率,故图4a只给出了FBSM和FEM对Y-Y和Z-Z两个平动方向在1000 Hz内频响函数计算结果的对比情况。 由图4可知,对于子结构间为刚性连接和弹性连接两种情况,FBSM对频响函数的计算结果均与FEM的对应计算结果吻合程度良好,即FBSM可对结构的力学环境进行准确高效地预示。 图3 算例结构 表1 算例结构单元属性 图4 两种方法计算结果对比情况 文中分别对处理子结构间为刚性连接和弹性连接两种问题的FBSM进行了理论推导,并就弹性连接的等效方法进行了讨论,且通过算例仿真验证了FBSM的正确性。结果表明,对于子结构间为刚性连接和弹性连接两种情况,FBSM均可对结构的力学环境进行准确高效的预示,且在处理具有弹性连接结构的力学环境预示问题时,可采用空间梁单元等效弹性连接。该研究所得的结论具有一定的理论研究和工程应用价值。2 弹性连接FBSM推导








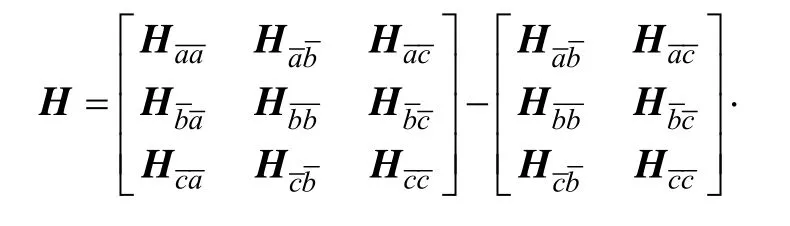

3 弹性连接等效方法


4 算例验证




5 结语

