动态价格下Logistic生长模型的捕获问题*

张 广，张 敏，宋冰洁

(1．天津商业大学 理学院，天津 300134；2．天津商业大学 经济学院，天津 300134)

1 引 言

近年来，如何有效利用鱼类、虾类这样的渔业资源，实现可持续开采、较好经济效益的同时不造成劳动成本的浪费，一直是生物学家和经济学家关注的热点问题. 早先就有著名的生物学家Malthus(1798)和P.F.Verhulst(1938)对生物种群数量的变化过程进行了研究，建立了众所周知的Malthus模型和Logistic模型. 此类模型均描述的是种群在自然环境下的增长规律，未考虑种群受人类开发这个因素. 而在现实生活中，尤其渔业资源是受人类开发利用的. M.B.Schaefe最早提出了金枪鱼的一般生产模型，即对金枪鱼的开发利用模型. 在此基础上，1954年Gordon[1]提出了新的经济理论——净利润等于总收入减去总成本，把价格成本引入了生物经济模型,并假定所收获的单位生物量价格和捕捞成本是常数. 1969年Smith提出了一种新的数学模型，它利用净利润来描述人类行为与种群开发的动态关系，即渔业赚钱，捕鱼者增多(种群开发增强)，自然捕获量也增多. 鱼多了价钱就会下降，进而渔业没钱可赚，捕鱼者随之减少(种群开发减弱). 也就是说种群的密度(或数量)和捕获努力量(种群开发程度)之间是一个自反馈控制，即开放式渔场的自反馈捕获模型. 在文献[2-4]中都对开放式渔场的自反馈捕获模型进行详细的定性分析和研究，并且文献[3]从经济角度出发，开始将价格作为变量处理. 而事实上，市场价格一成不变显然是不可能的. 所捕获鱼的价格与消费者的需求量，鱼的市场供给量有密切的关系. 在此基础上，2001年王克，范猛等[5]在借鉴文献[2，6]的基础上对价格进行新处理——受供求关系影响的代数形式的价格. 而后大量文献[7-15]从经济效益角度出发研究捕获问题，里面的价格均以代数形式处理. 与此同时也有文献[16]和文献[17]分别以最大可持续量为目标对带有周期系数单种群和经济效益最大时种群的捕获时间进行研究. 综上可以看出有众多文献对种群捕获问题都进行了研究，经济效益是大家所普遍关注的重点问题，进而价格问题也显得尤其重要. 虽然已有的文献可以反映出价格是受供求关系影响的，但是经济系统是动态的，经济变量是随时间变化而改变的，故价格以代数形式处理并不符合市场规律，文献[18]中建立了由微分方程刻画的非线性价格调整模型. 根据价格理论，需求曲线是向右下方倾斜的，表示商品的需求量和价格是反方向变动的关系. 同样供给曲线是向右上方倾斜的，表示商品的供给量和价格是同方向变动的规律. 需求曲线和供给曲线是线性或非线性的，在不影响结论的前提下，为简化分析，经济学中大多采用线性处理. 本文以下也将按线性处理.

本文基于价格受市场供求关系的变化，首先建立一种新型的动态价格下的捕获模型. 其次计算出均衡点并对稳定性进行了证明和动力学分析. 再次，做了数值模拟且从生物经济学角度进行了解释. 最后得出结论给出建议.

2 模型的建立

开放式渔场的自反馈捕获模型[1]为：

(1)

其中，s表示t时刻某类鱼种群的密度或数量，E表示t时刻捕获努力量，p表示价格，w表示单位投入成本，v是正常数，表示捕获努力量与净利润的大小成正比.

模型(1)中，价格p是常数. 在实际的市场经济中，市场需求和市场供给决定了市场的出清价格. 这里假设需求曲线是线性的，即qd=a+bp，其中b<0. 供给曲线是线性的，即qs=c+dp，其中d>0. 市场价格时刻受供给量和需求量的影响，当需求量大于供给量时，则价格上升；当供给量大于需求量时，则价格下降．文献[18]也讨论了相同的价格问题．在文献[2]中有：

(2)

结合供给曲线和需求曲线，式(2)变成

(3)

进而得到新的动态价格下的捕获模型：

(4)

这里Logistic规律刻画生物种群增长. 其中，系数r代表种群内生增长率，k代表环境的最大承载量(或饱和水平)，即代表着栖息地可以容纳的最大种群数量.

3 均衡点及其稳定性分析

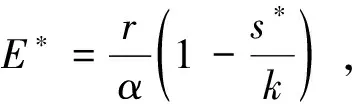
定理1假设a>c,b<0，d>0，那么模型(4)有且仅有一个正均衡点.

证明由

可解得：

E*=(s*,E*,p*).

其中，

证毕.

定理2定理1的条件成立，那么均衡点E*(s*,E*,p*)是局部渐近稳定的.

证明

模型(4)的雅克比矩阵为

在均衡点E*(s*,E*,p*)处相应的特征方程为：

a0λ3+a1λ2+a2λ+a3=0，

其中，

这里

其中，a0=1>0，因为b<0,d>0故而-β(b-d)>0，又加上r,k,s*均大于0，因此a1>0. 因为v,w,r均大于0且s*0.

Δ2=

证毕.

4 全局动力学分析

绘制均衡捕获努力量的倾斜面、均衡种群数量的曲平面、均衡价格的水平面，见图1．

根据图1分别从三个均衡面进行分析：

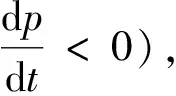
分析后得出在八个卦限中，生物种群数量、捕获努力量和价格水平的增减性见表1．

图1 (a)、(b)分别表示捕获努力量、种群数量及价格均衡空间视图及其旋转图

sEpsEp一 ↑↑ ↓ 二 ↓ ↑ ↓三 ↓ ↓ ↓ 四↑ ↓ ↓五 ↑ ↑ ↑ 六 ↓ ↑ ↑七 ↓ ↓ ↑ 八 ↑ ↓ ↑

为了体现模型(4)在经济意义下的优势，现将新型动态价格下的模型(4)和开放式渔场常数价格下的模型(1)进行比较，选取模型(4)均衡价格处的截面图与模型(1)常数价格下的二维图，并将这两个图画在同一坐标系下，见图2. 从图2中可以看出，在有相同的种群数量和捕获努力量的前提下，均衡价格下和常数价格下，经过一系列的循环，都能达到各自的均衡点处，但均衡点是不一样的．在捕获生物种群相同数量S3时，均衡价格下的捕获努力量要低于常数价格下的捕获努力量，这对于如何控制捕捞行业的捕捞成本是有一定参考价值的.

5 数值模拟与生物经济学解释

接下来考虑具体系统

来说明捕获努力量、种群数量、价格三者变化情况.

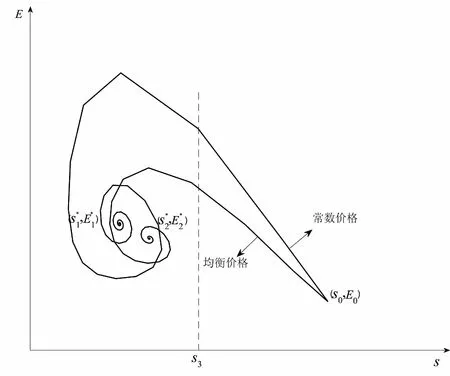
图2 表示均衡价格、常数价格下生物经济图，其中常数价格来源于模型(1)

这里r=3,k=5,α=0.5,v=1,w=3,β=1,a=4,c=1,b=-1/2,d=1/2，故v>0,β>0,a>c,b<0,d>0满足条件. 按照介绍的计算法可以计算出正均衡点E*(2,3.6,3)并且可以得出是局部渐近稳定的(这里以初值s0=2,E0=4,p0=4，在第二卦限为例做具体详细说明). 用Matlab仿真结果证明最后趋近于正均衡点，见图3．

图3 (a)、(b)表示系统初值在第二卦限不带均衡面、带均衡面的仿真模拟结果

生物经济学解释：

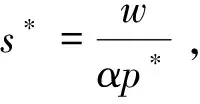
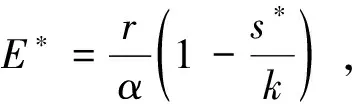
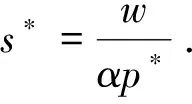
初值分别在八个卦限的Matlab仿真对比结果见图4．

从图4中可以看出，初值在八个卦限时最终都趋近于了正均衡点E*(2,3.6,3). 说明捕获努力量、种群数量、价格三者无论初值在哪个象限，是否存在利润的情况下最终都将趋于均衡点.

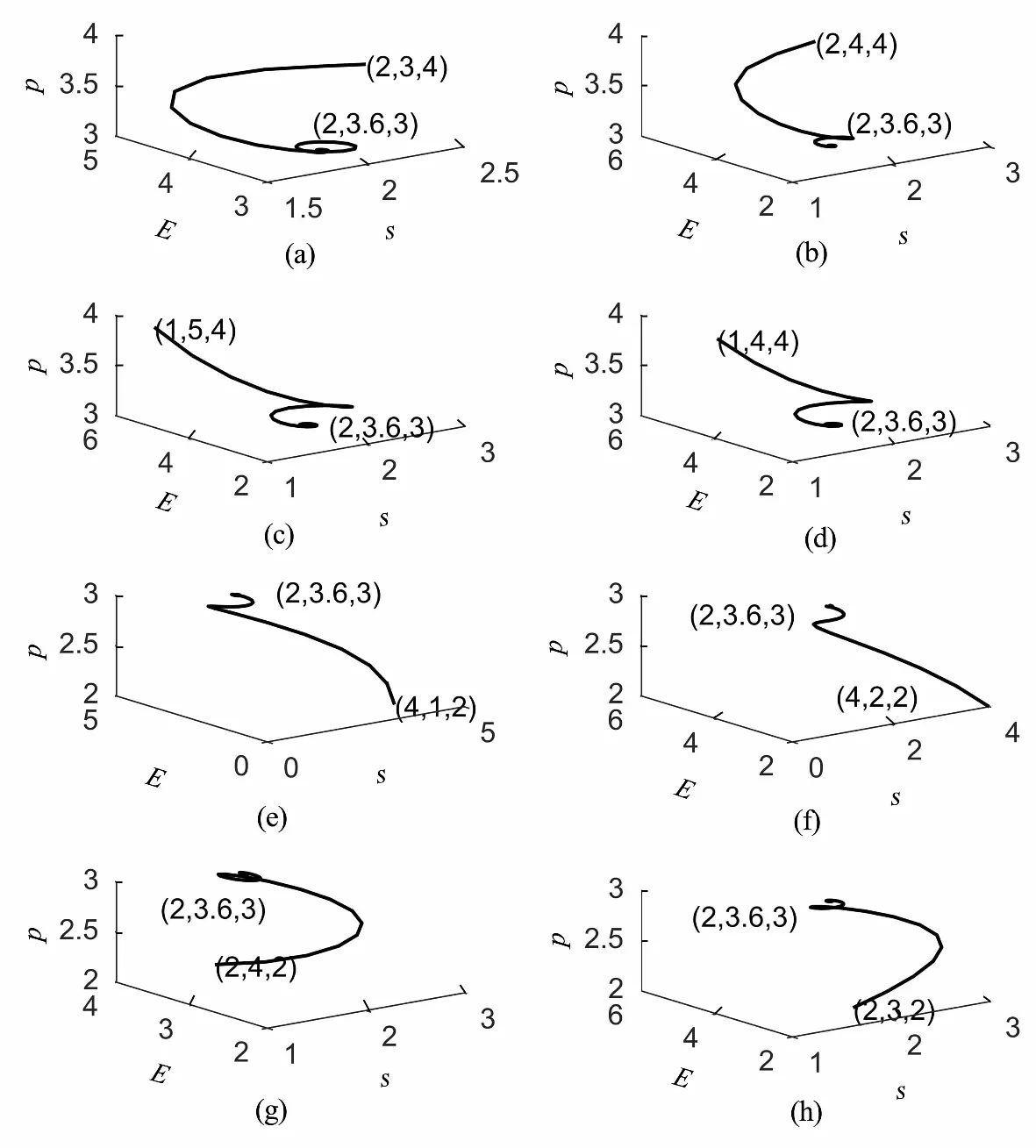
图4 (a)～(h)分别表示系统初值在第一、二、三、四、五、六、七、八卦限仿真模拟结果

6 结 论

本文从价格理论角度出发，考虑市场价格受供给和需求的影响，建立了一种新的动态价格下的捕获模型，进而理论证明了系统仅有一个正均衡点且是渐进稳定的，并从数值模拟和生物经济学两个角度出发，验证了无论初值在哪个卦限最终都趋向于均衡点，来进一步说明均衡点的稳定性. 更重要的是发现如果捕获相同数量的生物种群，那么在均衡价格下的捕捞努力量要低于常数价格下的捕捞努力量，这将为捕获问题的优化管理提供有价值的理论借鉴.