基于三类模型的四大银行股票收益率预测研究*

李雄英, 陈小玲, 曾凯华

(1.广东财经大学 统计与数学学院，广东 广州 510320；2.广东省技术经济研究发展中心,广东 广州 510070)

1 引 言

在股票市场，不少学者关心股价的变化和股价的预测，股价的不确定性变化往往又表现为市场的波动.由于股票收益率序列比股票价格序列能更好地体现股票市场的波动性,因此，在股票市场,对股票收益率进行建模预测相对于股票价格预测来说有着重要的研究价值.

预测的理论方法多种多样.有的学者研究人工神经网络预测模型、灰色预测模型、支持向量机预测模型等；有的学者研究时间序列方法，如ARIMA模型、ARCH模型；也有不少学者提出了一种组合预测模型，如ARIMA和SVM相结合的预测模型、ARIMA和BPNN组合的预测模型等[1].近年来，国内也有不少用ARMA模型、ARCH 模型和GARCH模型来研究时间序列数据变化和波动规律的成果.例如，吴玉霞和温欣(2016)[2]运用ARIMA模型预测了股票价格变动的规律和趋势，预测效果较理想.鲁万波(2006)[3]应用非参数 GARCH模型能较好地预测中国股市的波动性.王蒋凤和吴群英(2011)[4]运用GARCH类模型对沪深300指数序列的波动性、收益率进行拟合与预测，获得理想的效果.魏红燕和孟纯军(2014)[5]运用GARCH模型研究人民币对美元的汇率预测，预测结果比较理想.罗永恒(2013)[6]应用ARMA模型较好地反映了中国农产品价格指数的动态变化.付燕和栗锋(2012)[7]运用ARMA模型对我国体育股票价格进行预测分析.贺本岚(2008)[8]应用ARIMA与ARCH模型预测股票价格，结果表明ARCH 模型相比ARIMA模型的预测效果更满意.闫冬(2012)[9]将GARCH模型与ARMA模型相结合，提出 ARMA-GARCH 组合预测模型，研究表明ARMA-GARCH 预测模型有效地刻画了上证指数的短期变化.而在股票价格波动性的预测能力方面上，将ARMA模型、GARCH 模型以及ARMA-GARCH组合模型相比较的研究成果并不多.而大多数时间序列预测模型都是以ARMA或GARCH模型为基础，因此比较ARMA模型、GARCH模型和ARMA-GARCH模型的预测效果具有重要的意义.

本文旨在研究ARMA模型、GARCH 模型对中国四大银行股票价格波动的预测能力，通过以中国四大银行股票每日的收盘价提取样本研究对象，分别建立ARMA模型、GARCH 模型以及ARMA-GARCH模型对收益率序列进行预测与分析.首先，用ARMA模型来刻画t时刻的收益率；再检验收益率序列是否存在条件异方差性，从而确定建立GARCH模型；接着由于ARMA模型残差存在ARCH效应以及GARCH模型的均值方程系数不显著，从而建立ARMA-GARCH组合预测模型；最后通过模型比较表明，对四大银行股票收益率预测研究，拟合效果上，ARMA-GARCH模型的拟合优度最好；预测效果上，ARMA模型预测精度最好，其次是ARMA-GARCH模型.

2 时间序列模型简介

2.1 ARMA模型[10]

ARMA模型是一类常用的随机时间序列模型，由美国统计学家Box和Jenkins创立，亦称Box-Jenkins方法.ARMA(p,q)模型的一般表达式为：

rt=φ1rt-1+φ2rt-2+…+φprt-p+ut-θ1ut-1-…-θq．

(1)

该模型中p为自回归部分的阶数，q为移动平均部分的阶数，因此记为ARMA(p,q).

运用该ARMA模型的前提条件是，作为分析对象的时间序列是一组零均值的平稳序列.但现实中存在大量的非平稳的时间序列.因此，在建立ARMA模型之前，需要对序列进行平稳化处理.

2.2 ARCH效应与GARCH模型[11]

在金融市场中，股价或市场具有波动率聚集的特点.1982年Engle最早提出了运用ARCH模型对金融市场波动的条件异方差性进行刻画.ARCH模型，它的主要思想是扰动项是前后不相关的，它的条件方差依赖于它的前期值的大小.ARCH(q)模型的一般表达式为：

(2)

式中，假定εt是独立同分布的标准正态分布，α0>0,αi≥0(i=1,2,…,q).

关于ARCH效应的检验，即对均值方程的残差平方序列进行条件异方差性检验.若发现存在显著的ARCH效应，则可以建立一个波动率模型.但ARCH模型有一个显著的特点，就是通常拟合的模型阶数q较大，为了解决这个问题，1986年Bollerslev在Engle的ARCH模型基础上提出了广义自回归条件异方差模型-GARCH模型.

对于一个对数收益率序列rt，令at=rt-μt为t时刻的新息.称at服从GARCH(m,s)模型，若at满足：

(3)

式中，εt是均值为0，方差为1的独立同分布序列，α0>0,αi≥0,βj≥0,α0>0,αi≥0,βj≥0，且

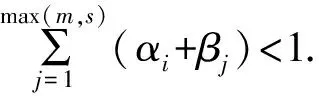
2.3 ARMA-GARCH模型[12]

ARMA-GARCH 模型表示的是序列的均值应用 ARMA模型，条件方差应用GARCH模型.因此，ARMA-GARCH 模型的基本结构表示为：

(4)

3 实证分析——以中国四大银行为例

3.1 数据选取与基本统计分析

本文选取2007年10月1日-2017年10月1日的中国银行、中国工商银行和中国建设银行的股票每日收盘价以及中国农业银行2010年7月15日-2017年10月1日的股票每日收盘价作为样本数据，其中最后2天的数据作为测试数据，数据来源于雅虎财经网.本文研究股票市场的波动，以股票市场的日收益率作为考察变量，股票市场的日收益率以相邻两日收盘价的对数一阶差分来表示，并以Rt作为第t日的股票日对数收益率.日对数收益率组成新的样本时间序列，对该序列进行基本的统计分析，得到其基本描述统计分析结果及其时序图，分别见表1和图1.

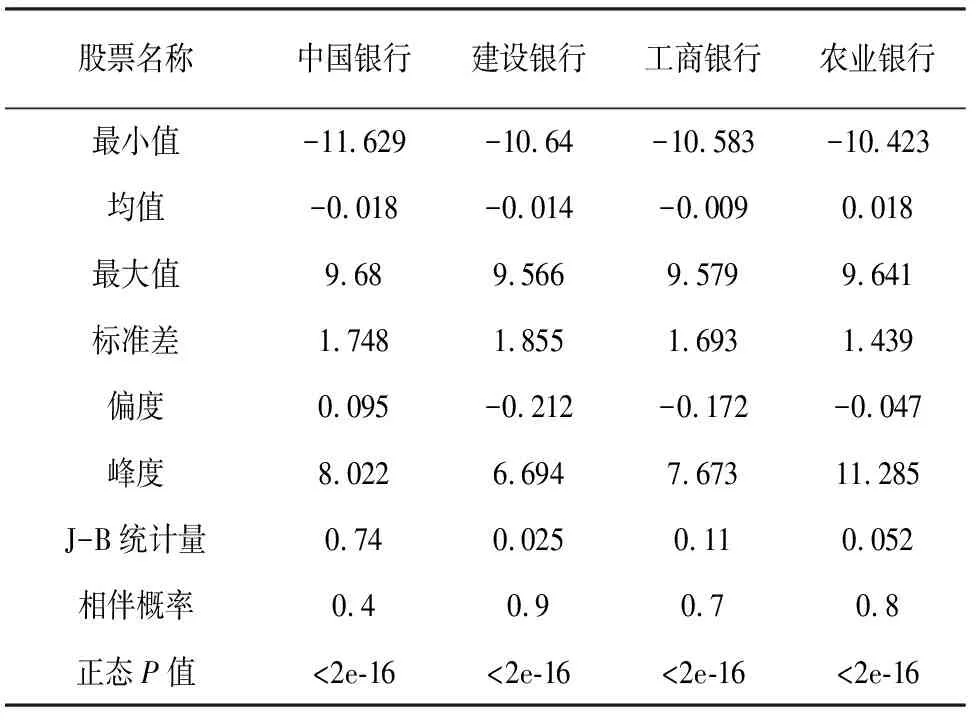
表1 中国四大银行日对数收益率的基本统计特征

由表1可知，中国银行的偏度为0.095，接近于0，其他三大银行的偏度均小于0，而四大银行的峰度值均大于3，说明其日对数收益率具有尖峰厚尾特征，正态性检验所得的P值均接近于0，这说明至少可以在99%的置信水平下拒绝序列为正态分布的零假设，即可以认为中国四大银行的日对数收益率序列均不服从正态分布，其所对应的股价序列并不是完全随机的.

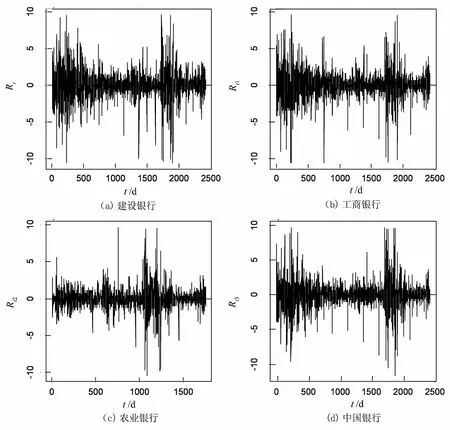
图1 中国四大银行日对数收益率时序图

由图1四大银行的收益率时序图上可以看出，各银行的收益率在零均值附近上下波动，可以初步判断四大银行的日收益率是平稳的.

3.2 ARMA模型的建立与分析

1) 平稳性检验

利用时间序列分析进行建模,首先需要对数据平稳化.而仅从时序图中判断序列的平稳性是不严格的，因此建模前必须先检验序列的平稳性.接着采用ADF单位根检验法进一步对该日对数收益率序列进行平稳性检验，检验结果见表2.

表2 各银行日收益率序列的单位根检验

由表2可见，显然各序列都可以在0.01的显著性水平下拒绝原假设，接受备择假设，即序列不存在单位根，则认为各序列{Rt}是平稳的.因此，各银行的日对数收益率序列均可以考虑建立ARMA(p,q)模型.

2)ARMA模型识别与参数估计

对模型进行识别拟合与估计，可以利用序列的自相关系数(ACF)和偏自相关系数(PACF)识别ARMA模型的阶数，并结合AIC信息准则择优选择模型，即AIC值越小其精度越高，拟合得较好.因此，结合各序列的ACF和PACF图以及AIC信息准则，最终选择最优的ARMA(p,q)模型分别为建设银行ARMA(2,2)，工商银行ARMA(2,4)，农业银行ARMA(2,2)，中国银行ARMA(3,1).其中四大银行模型估计结果见表3.

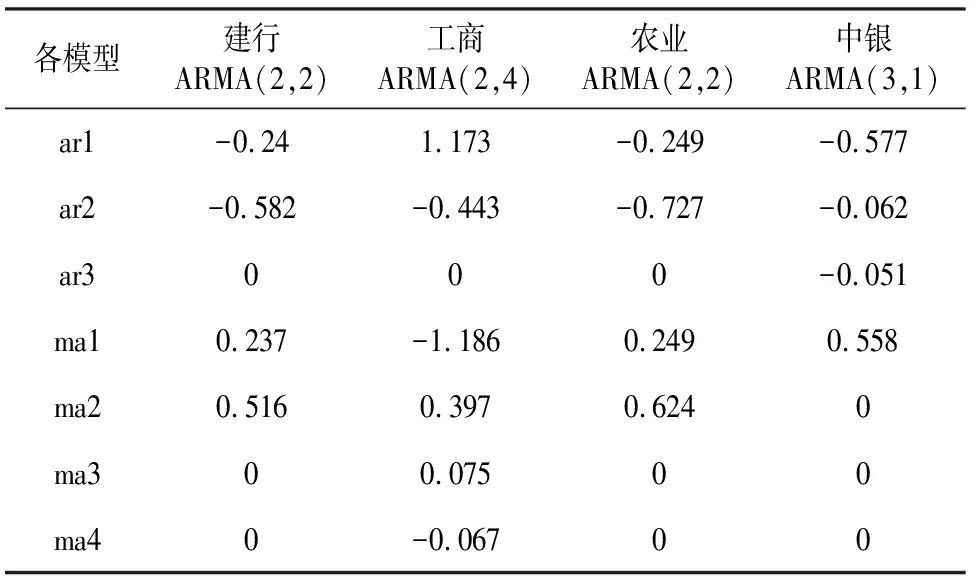
表3 ARMA模型参数估计结果

由表3可知，以中国银行的日对数收益率为例，最终选择ARMA(3,1)模型，即

rt=-0.577rt-1-0.062rt-2-0.051rt-3+

at+0.558at-1．

(5)

3)ARMA模型检验

对所建立的ARMA模型优劣的检验，是通过对原序列与所建立的ARMA模型的残差序列{at}进行检验来实现的.若残差序列具有随机性，就意味着所建立的模型已包含原时间序列的所有趋势，从而说明所建立的模型对原时间序列的描述是合适的充分的.本文中对残差的这种随机性检验采用的是Box-Ljung检验法.四大银行的ARMA模型的残差序列的随机性检验结果见表4.

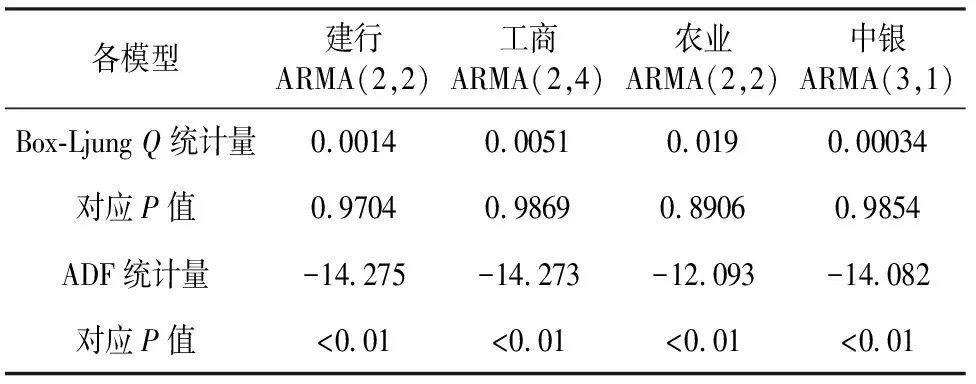
表4 模型残差相关性与平稳性检验

由表4可知，各银行的日收益率序列拟合的模型，其对应的残差序列的Box-Ljung检验的P值均大于0.05，证实了各模型的残差序列没有显著的相关性，从而模型建立是合理的.因此，可以应用上述ARMA模型预测各四大银行的日收益率.

3.3 GARCH模型的建立与分析

从基本统计分析中，得到中国四大银行的日对数收益率具有尖峰厚尾特征，且各序列均不服从正态分布.从图1时序图中可以发现，除了观察到各收益率序列在零均值附近上下波动之外，还有一个明显的特点，就是波动的聚集性.因此，需要进一步判断日收益率序列是否具有条件异方差性，以尝试通过波动率进行建模，从而达到改进模型的作用.

1)ARCH效应检验

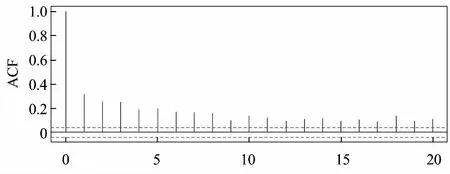
Lag

Lag

Lag

Lag

2)GARCH模型的建立

通过上述检验，发现各收益率序列均存在显著的条件异方差性，进而为了消除序列的异方差性，选取构建GARCH模型.本文选择建立GARCH(1,1)模型.借助R语言软件，得到各银行日收益率序列的GARCH(1,1)模型，其中残差项的分布分别选择了高斯分布、学生t分布、有偏学生t分布，3个模型都能较好地拟合了给定的数据，且3个拟合序列之间的相关系数都接近1，区别比较小.本文结合AIC最小原则选择模型，综合考虑，最后残差项的分布选择有偏学生t分布达到相对更优.各收益率序列的新息是服从有偏学生-t分布的GARCH(1,1)模型的参数估计结果见表5所示.

由表5可以看到，所有的参数估计，除了模型中的常数以外，其他参数都是高度显著的，说明GARCH(1,1)能较好地拟合数据.其中，以中国银行股票的日对数收益率序列为例，应用带有偏学生t分布的新息，拟合的GARCH(1,1)模型为：

(6)

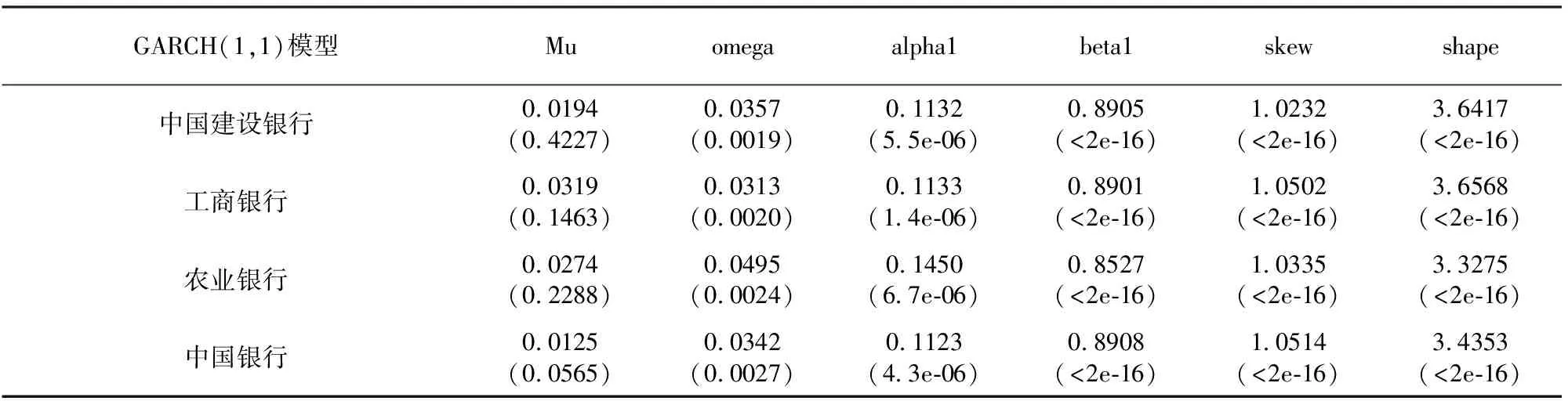
表5 GARCH模型估计结果

注：括号内为估计模型系数的概率

3)模型的检验

接下来，对GARCH(1,1)模型的残差与残差平方进行相关性检验.标准化残差的Ljung-Box统计量和它们的平方序列都不能拒绝该模型，因为其对应的P值均大于0.05，从而认为各模型的残差序列不存在ARCH效应，说明以上GARCH(1,1)模型消除了残差序列的条件异方差性，模型的拟合是充分的.

3.4 ARMA-GARCH模型的建立与分析

1) ARMA-GARCH模型的建立

正如前文所述，在建立纯时间序列ARMA模型时，显然忽略了序列中存在ARCH效应，而仅仅的ARMA模型并不能处理序列的条件异方差性.对于存在ARCH效应的序列，若仅仅是通过波动率进行建模，如上文仅仅对股票的日对数收益率序列建立GARCH(1,1)模型，由表5可知，其常数项并不显著，即仅构建波动率模型，其均值方程是不显著的.因此，本文考虑在建立ARMA均值方程的基础上，对均值方程的残差项建立GARCH模型以消除条件异方差性，即通过建立ARMA-GARCH模型对样本日对数收益率序列的ARMA模型进行改进.

对前文ARMA模型残差进行ARCH效应检验，将Ljung-Box统计量应用于各ARMA模型的残差平方序列，建行、工商银行、农业银行与中国银行的4个ARMA模型的残差平方序列的Ljung-Box统计量分别为Q=260，Q1=160，Q2=130，Q3=170，其对应的P值均接近于0，说明残差序列存在显著的序列相关性，显然残差序列存在ARCH效应.于是考虑建立ARMA-GARCH组合预测模型.残差项的分布仍然选择有偏学生t分布，各收益率序列的新息是服从有偏学生-t分布的ARMA-GARCH模型的参数估计结果见表6.

表6 各ARMA-GARCH模型的参数估计结果

同样地，根据表6，以中国银行股票的日对数收益率序列为例，应用带有偏学生t分布的新息，改进后的ARMA(3,1)-GARCH(1,1)模型为：

(7)

2)模型检验

在得到改进的ARMA-GARCH模型后，对其对应模型的标准化残差及其平方进行相关性检验.四大银行的股票日对数收益率序列的ARMA-GARCH模型对应的标准化残差的Ljung-Box统计量和它们的平方序列都不能拒绝原假设，说明ARMA-GARCH模型的拟合是充分的.其中，以中国银行股票日对数收益率序列为例.从估计模型标准化残差的时序图、QQ图及其相关图中可以看出，标准化残差序列是白噪声序列，不存在序列相关性，而且其标准化残差平方序列也不存在序列相关性，已经消除了条件异方差性，从而说明所拟合的ARMA(3,1)-GARCH(1,1)模型是充分的.

3.5 模型的比较与讨论

3.5.1 样本内比较

如果数据分析的目的是为了研究一个时间序列的动态结构，那么可以用样本内方法来比较不同的模型.样本内比较法就是利用所有数据来进行模型估计和比较，比如信息准则(如AIC和BIC)和残差方差的估计.如果选定其中一个准则，那么它的值越小，模型就越好.本文采用的AIC准则对以上3个模型进行样本内比较，其值见表7.

表7 样本内比较

从表7可知，根据AIC准则，对股票的日对数收益率序列建立波动率方程GARCH模型相比要优于建立ARMA模型.GARCH模型的AIC值比较于ARMA 模型的AIC值有了比较大的下降，说明四大银行的股票日对数收益率序列存在波动率集聚现象且GARCH模型可以更好地解释并消除条件异方差.根据表7，改进的ARMA-GARCH组合预测模型相比单纯的ARMA模型与单纯的GARCH模型也都更优.因此，根据AIC准则，即在样本内比较时，ARMA-GARCH模型的拟合效果更理想.

3.5.2 样本外比较

若建立时间序列模型是为了预测，则进行模型比较就要考虑模型的预测能力.本文采用均方误差(MSFE)和平均绝对误差(MAFE)2个指标来衡量模型预测效果的好坏，对于不同的模型，若预测的MSFE或MAFE越小，则说明预测精度越高[13]. 把最小MSFE或最小MAFE对应的模型作为这组数据的最好模型.其中，这2个指标反映预测值与实际值之间的误差大小，其定义分别为：

(8)

(9)

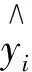
根据各模型对股票日对数收益率的测试集的预测，计算了各模型预测的均方误差、平均绝对误差，下面给出3个模型超前两步预测时，其在第一步预测中对应的预测误差的均方(MSFE)与平均绝对预测误差(MAFE)，整理见表8.

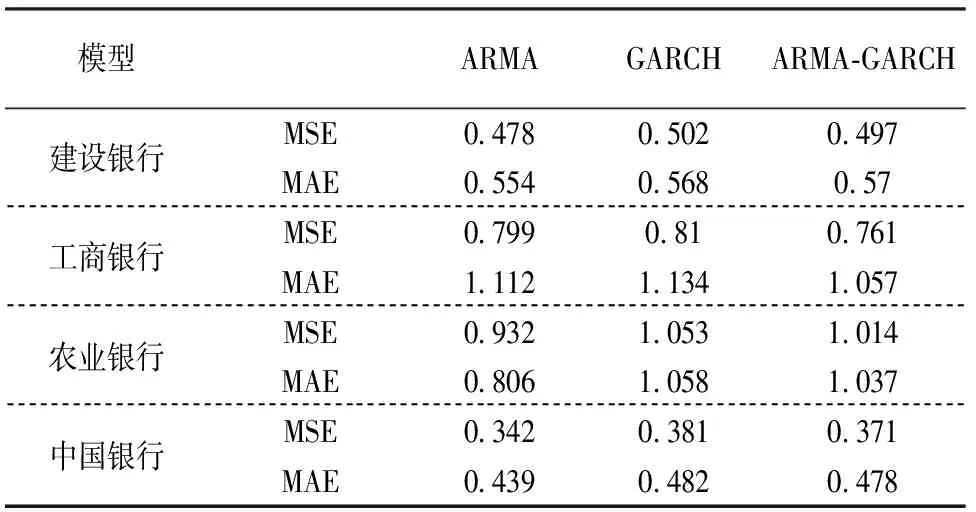
表8 样本外比较

根据表8可以得到，ARMA模型、GARCH模型与ARMA-GARCH模型这3个模型的预测效果差别不大.整体上，ARMA模型的预测效果更优，其中ARMA-GARCH模型是在ARMA模型的均值方程基础上，对残差项加入GARCH模型的波动率方程，但其预测效果也并没有得到提升.因此，从预测精度上看，ARMA模型的预测效果最好，波动率建模的预测效果并没有得到提高.

4 结 论

本文运用时间序列分析的预测方法，通过对中国四大银行的股票日对数收益率序列进行实证分析可以发现，ARMA模型、GARCH模型以及改进的ARMA-GARCH模型均能对四大银行的股票日对数收益率序列进行拟合与预测分析，具体可以得到以下结论：

1)在模型拟合效果方面，对四大银行股票的日对数收益率序列建立GARCH模型相比要优于建立ARMA模型，而建立改进的ARMA-GARCH模型，与建立单一的ARMA模型、单一的GARCH模型相比，ARMA-GARCH模型的拟合优度都更优更理想.这是由于四大银行的股票日对数收益率序列存在波动率集聚现象且GARCH模型可以更好的解释并消除条件异方差，也说明ARMA-GARCH模型和GARCH模型能更好地反映这个时间段四大银行日股价的实际波动情况.

2)在模型预测效果方面，ARMA模型、GARCH模型以及ARMA-GARCH模型各自的均方预测误差与平均绝对预测误差都比较小且各模型之间的预测误差均相差在1%左右.整体上，在预测四大银行的股价上，ARMA模型的预测效果最优，其次ARMA-GARCH模型.

综上所述，ARMA模型对于四大银行股票的波动性、股票收益率的预测效果比较好，但ARMA模型对股票收益率预测的拟合优度均远远高于GARCH和ARMA-GARCH模型.GARCH和ARMA-GARCH模型对于股票收益率序列可以很好地消除条件异方差，ARMA和GARCH模型结合的ARMA-GARCH模型在拟合效果和预测能力上都取得更理想的效果.