基于个体兴趣度差异和辟谣机制的谣言传播模型
冉茂洁,刘 超,黄贤英,刘小洋,杨宏雨,张光建
(重庆理工大学 计算机科学与工程学院,重庆 400054)(*通信作者电子邮箱candyranmj@163.com)
0 引言
谣言通常是指利用各种通信手段,对公众关心、关乎公共利益的问题、事情等未经证实的阐述[1]。互联网的快速发展及各社交软件的流行极大提升了谣言的传播速度与传播范围,严重影响社会结构及经济市场稳定[2-3], 因此,研究谣言的传播机理,为抑制谣言传播提供理论指导具有十分重要的意义。
由于谣言传播与传染病扩散的高度相似性[4],许多学者借鉴生物传染病学中的仓室建模法并考虑人类社会行为属性建立谣言传播模型,揭示谣言传播的内在规律。文献[5-7]在SIR(Susceptible-Infected-Removal)模型基础上引入心理因素,证实个体心理差异影响个体传播谣言的概率。Afassinou[8]基于SEIR(Susceptible-Infected-Exposed-Removed)模型考虑个体受教育程度对传播的影响发现谣言传播规模与个体受教育程度呈正相关。在大数据时代,信息的爆发式增长加大了个体遗忘信息的概率[9]。Ebbinghaus[10]的研究结果显示:遗忘在学习之后即开始,遗忘进程不均匀,因此,个体遗忘在谣言传播过程中影响巨大。Nekovee等[11]首次将自发性遗忘机制引入谣言传播模型,证明了遗忘率对基本再生数存在性的重要影响。Zhao等[12]基于常数遗忘率建立SIHR(Susceptible-Infected-Hibernator-Removed)传播模型得出遗忘将降低谣言最大影响力。Zhang等[13]进一步在时变性遗忘率基础上分析谣言传播证明了时变遗忘机制下谣言的传播范围更广。由于媒体报道对民众行为有巨大影响[14],许多学者分析了谣言传播过程中的媒体干扰:陈华[15]认为媒体干扰影响个体传播行为,基于SIR模型提出媒体播报干扰下的谣言传播模型,证实媒体播报降低传播者的传播力度;Zhao等[16]对谣言传播过程中的媒体辟谣行为进行分析得出媒体影响力差异导致辟谣效力差异,最终导致谣言传播范围差异。
虽然以上研究成果对分析谣言传播机理作出了巨大贡献,但仍有许多影响谣言传播的关键因素,如个体兴趣度差异等未考虑进谣言传播模型。在整体社会环境中,个体生活经历、受教育程度等的差异将导致个体兴趣的差异,进而影响个体行为[17]。互联网的飞速发展极大降低信息传播成本,各领域均可借助网络工具传播谣言,这进一步加大了兴趣度差异在传播过程中的影响作用;同时谣言传播过程中政府、权威媒体发布的辟谣信息可降低谣言的危害力度,樊重俊等[18]和王筱莉等[19]指出辟谣行为可有效降低谣言最大影响力,最终降低谣言传播范围,所以在构建谣言传播模型过程中辟谣机制不可忽略。
鉴于以上原因,本文在考虑个体兴趣度差异的基础上引入辟谣机制,建立基于个体兴趣度差异和辟谣机制的IWSR(Ignorant-Weak spreader-Strong spreader-Removal)谣言传播模型。运用微分动力系统理论,得出模型平衡点稳定的基本条件,最后通过数值仿真验证理论分析的正确性,并在WS(Watts-Strogatz)小世界网络和BA(Barabási-Albert)无标度网络中分析了网络拓扑结构对谣言传播的影响。
1 IWSR模型
1.1 模型的建立
兴趣度指个体对事物的感兴趣程度,而个体的生活、教育经历等与个体的兴趣爱好密切相关,因而对同一事物个体的兴趣存在差异性[20]。本文在考虑个体兴趣度差异的基础上引入辟谣机制,建立了IWSR谣言传播模型。借鉴传播学中的仓室建模法,将传播网络中的人群划分为4类:无知者(I-node,未接受过谣言的个体),弱传播者(W-node,谣言信息的低兴趣度个体)、强传播者(S-node,谣言信息的高兴趣度个体)、辟谣者(R-node,清除或澄清谣言信息的个体)。I(t)、W(t)、S(t)、R(t)分别表示t时刻4类人群的比例,在本文中将I(t)、W(t)、S(t)、R(t)分别用I、W、S、R指代。如图1,无知者分别以不同的概率被感染为强传播者或弱传播者;传播者以一定概率转为辟谣者。对IWSR谣言传播模型中各仓室间的转换规则作如下描述:
1) 新加入个体以概率δ成为传播网络中的无知者;传播网络的4类人群以相同概率移出传播网络。
2) 在各辟谣信息影响下,强传播者怀疑谣言并以概率β转为弱传播者。
3) 强传播者S以概率λ2影响未知者I使其成为强传播者;弱传播者W以概率λ1影响未知者I使其成为弱传播者,且可假定λ2>λ1。
4) 受政府辟谣信息影响,各传播者鉴于政府的权威性以概率α选择相信政府停止传播谣言并成为辟谣者R。
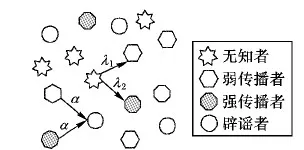
图1 无知者、传播者各自的转移概率
根据上述状态转换规则,得到传播网络中谣言传播的状态转换图,如图2。

图2 谣言传播过程中各仓室间的状态转换
根据图2建立谣言传播的微分动力方程组模型:
(1)
借鉴传播学中基本再生数的定义,定义谣言传播模型的基本再生数为单个谣言传播者在其传播周期内所感染的未知者个数,根据文献[21]提出的方法得该谣言传播模型的基本再生数为:
R0=max{λ1/δ,λ2/(δ+β)}
(2)
由式(1)可知,该传播网络的规模保持恒定,假定I(t)+S(t)+W(t)+R(t)≡1,式(1)转化为:
(3)
假设各参数均为正数,初始条件为I≥0,W≥0,S≥0,正向不变集为:
Ω={(I,W,S):I≥0,W≥0,S≥0,I+W+S≤1}
1.2 平衡点及其稳定性分析
当R0<1时,式(3)存在无传播平衡点E0=(I,W,S)=(1,0,0)。
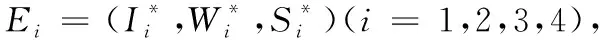
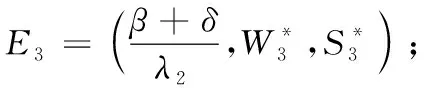
其中:
定理1 1) 当R0<1时,E0在Ω内局部渐进稳定。

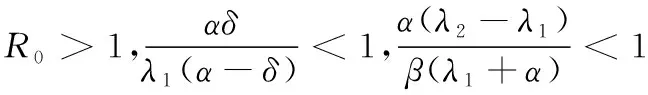
证明 系统(3)的Jacobi矩阵为:
(4)
其中
J11=-λ1W-λ2S-δ
J22=λ1I-α(1-I-W-S)+αW-δ
J33=λ2I-β-α(1-I-W-S)+αS-δ
1)式(4)在E0处对应的矩阵:
令
将Δi(i=1,2,3)定义为M0的i阶顺序主子式,则:
Δ1=|δ|=δ
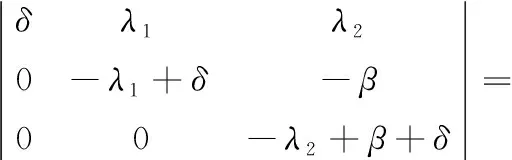
δ(-λ1+δ)(-λ2+β+δ)
当R0=max{λ1/δ,λ2/(δ+β)}<1时,得Δ1>0,Δ2>0,Δ3>0,则M0为正定矩阵,由M0=-J0得J0的特征值全为负,根据Hurwitz判据[22]E0局部渐进稳定。
2) 式(4)在E1处对应的矩阵:
其中
令
Δi(i=1,2,3)为M1的i阶顺序主子式,则:
Δ1=|λ1|=λ1

[(δ-λ1)(λ1(α-δ)-αδ)]/λ1
3) 式(4)在E2处对应的矩阵
其中
令
Δi(i=1,2,3)为M2的i阶顺序主子式,则:
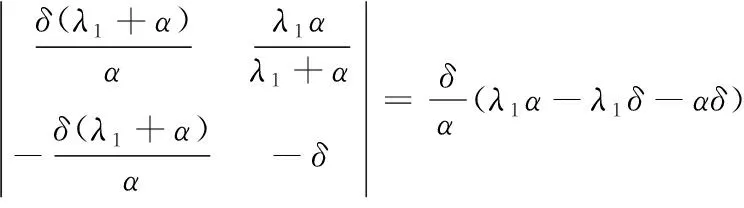


定理2 1) 当R0<1,λ1/δ>λ2/(β+δ)时,E0在Ω内全局渐进稳定。
2) 当R0>1时,E1在Ω′内全局渐进稳定,且Ω′={(I,W,S):I≤δ/λ1,W≥0,S≥0,I+W+S≤1}。
证明 1) 对平衡点E0运用Lyapunov函数
V(W,S)=W+μS
其中μ为正常数,V≥0恒成立,当且仅当W=0,S=0时V=0成立,则:
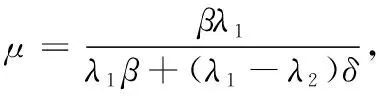
从而当R0<1,λ1/δ>λ2/(β+δ)时,V′≤0在Ω中恒成立,当且仅当W=0,S=0时V′=0成立。根据LaSalle不变集原理[23]以及极限方程原理得E0在Ω全局渐进稳定。
2) 针对平衡点E1考虑Lyapunov函数
其中k为正常数,V≥0恒成立,当且仅当I=I*,W=W*时,有V=0成立,则:
-λ1W(I-I*)2-λ1I*(W-W*)(I-I*)-
λ2S(I-I*)2-δ(I-I*)2+kλ1I(W-W*)2+
kλ1W*(I-I*)(W-W*)-kαR(W-W*)2-
kδ(W-W*)2=-λ1W(I-I*)2-λ2S(I-I*)2-
δ(I-I*)2+(kλ1W*-λ1I*)(I-I*)(W-W*)+
k(λ1I-αR-δ)(W-W*)2
令k=δ/(λ1-δ),则
δ(I-I*)2+k(λ1I-αR-δ)(W-W*)2
从而V′≤0在Ω′中恒成立,当且仅当I=δ/λ1,W=(λ1-δ)/λ1时V′=0成立。根据LaSalle不变集原理及极限方程原理得E1全局渐进稳定。
2 数值仿真分析
2.1 主要参数设置
在实验中设置I0=0.2,W0=0.2,S0=0.4,R0=0.2, 其中I0、W0、S0、R0分别指初始条件下各仓室用户所占比例。
2.2 数值仿真结果
为验证理论分析的正确性,下面对本文建立的模型进行仿真分析。
1) 当λ1=0.1,λ2=0.3,β=0.5,α=0.2,δ=0.2时,计算得平衡点E0=(1,0,0),且(λ1/δ)>(λ2/(β+δ))成立,由式(2)得R0=max{0.500 0,0.428 5}=0.5<1。根据定理2,E0全局渐进稳定。如图3(b),无知者比例缓慢增加达到峰值后趋于平稳,谣言传播者(W+S,弱传播者和强传播者之和)比例逐渐降低最终趋于零,即系统在E0点稳定,谣言最终消失。仿真结果与定理2的理论结果相符。最后选取12组不同I、W、S初始状态值,并在上述参数取值下模拟谣言传播,结果表明:在满足定理2条件下,传播网络中取不同传播者、未知者初始值时,其最终演化结果都将收敛于平衡点E0,如图3(a)。
2) 当λ1=0.3,λ2=0.4,β=0.1,α=0.5,δ=0.2时,通过简单计算可得到平衡点E1=(0.666 7,0.333 3,0),R0=max{1.5,1.3}=1.5>1,且I<δ/λ1成立。由定理2,E1全局渐进稳定。如图4(b),无知者比例快速增加达到峰值后缓慢下降最终在0.666 7处趋于平稳,谣言传播者比例先降低后缓慢上升最终在0.333 3处稳定,即系统稳定在点E1,谣言得到广泛传播。仿真结果与定理2的理论结果相符。最后在上述参数取值下选取12组不同I、W、S初始状态值进行仿真实验,得各曲线均收敛于平衡点E1,其结果如图4(a)。
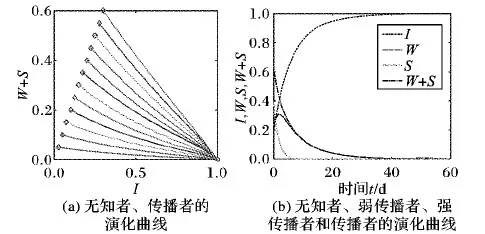
图3 R0<1时,I(t),W(t),S(t)和W(t)+S(t)的演化曲线收敛于E0

图4 R0>1时,I(t),W(t),S(t)和W(t)+S(t)的演化曲线收敛于E1
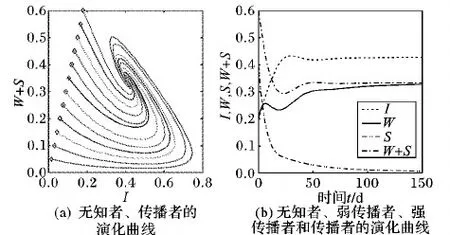
图5 R0>1时,I(t),W(t),S(t)和W(t)+S(t)的演化曲线收敛于E2

4) 下面将通过实验验证传播模型中的参数与谣言传播最终规模的关系。在实验中设置λ1=0.2,λ2=0.6,α=0.5,δ=0.2,同时令β值分别为0.2,0.3,0.5,0.7,得W+S随时间t的变化曲线如图6。在实验中设置λ1=0.2,β=0.3,α=0.5,δ=0.2,同时令λ2值分别为0.3,0.6,0.7,0.8,得W+S随时间t的变化曲线如图7。在实验中设置λ1=0.2,λ2=0.7,β=0.3,α=0.5,同时令δ值分别为0.2,0.3,0.4,0.5,得到W+S随时间t的变化曲线如图8。
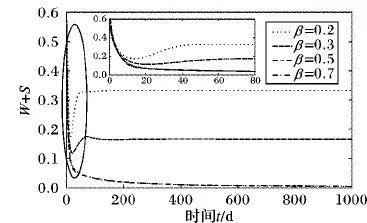
图6 不同β值时W(t)+S(t)随时间t的变化曲线
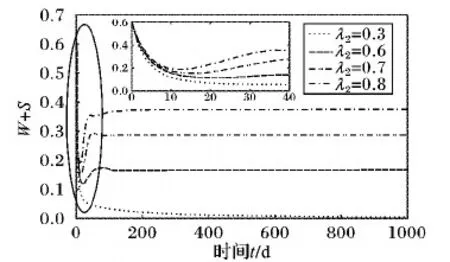
图7 不同λ2值时W(t)+S(t)随时间t的变化曲线
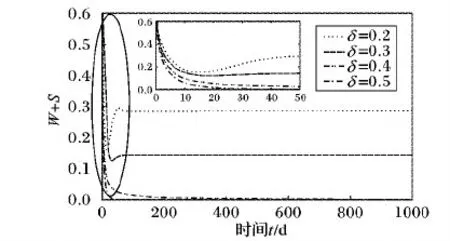
图8 不同δ值时W(t)+S(t)随时间t的变化曲线
由图6~8可知,增加β、δ值或降低λ2(λ1)值均能有效抑制谣言的传播。
5) 为研究在不同网络拓扑结构下各参数对谣言传播的影响,基于本文的建模思想,利用相关算法[24-25]生成WS小世界网络和BA无标度网络两复杂网络,并分别在各网络上模拟谣言传播。网络的相关拓扑特性参数见表1,度分布图如图9 (坐标为双对数坐标)。由图9可知,WS小世界网络的度分布服从泊松分布、聚类系数高;BA无标度网络度分布服从幂律分布、聚类系数低。

表1 各网络的相关特性参数
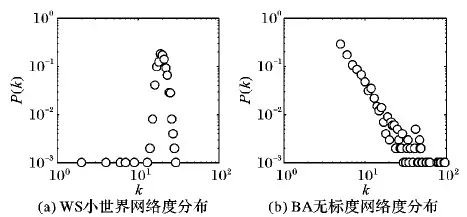
图9 各网络的度分布P(k)
为研究不同拓扑结构下δ值对谣言传播的影响力度,在实验中设置λ1=0.1,λ2=0.5,β=0.3,α=0.5,令δ值分别为0.1、0.5、0.9,在WS小世界网络和BA无标度网络上分别模拟谣言传播过程,得到W+S随时间t的变化曲线,如图10。
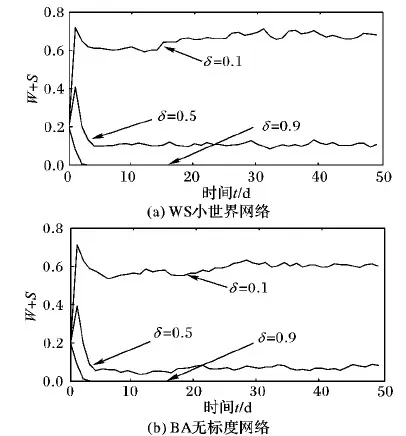
图10 当δ取不同值时,传播者在两复杂网络中随时间t的演化曲线
从图10可知,在WS小世界网络和BA无标度网络中,谣言传播者比例均随δ的增加而减少,即在谣言传播过程中加强政府或官方媒体的辟谣行为能有效降低谣言传播者比例,进而降低谣言的最大影响力。为研究不同拓扑结构下λ2对谣言传播的影响力度,在实验中设置λ1=0.1,β=0.3,α=0.5,δ=0.4,令λ2值分别为0.2、0.4、0.9,实验结果如图11所示。

图11 当λ2取不同值时,传播者在两复杂网络中随时间t的演化曲线
通过分析图11可得,谣言传播者比例在两仿真网络中均满足与λ2的正比例关系,即传播者比例随λ2降低而减少,所以提升个体对谣言的辨识能力可有效减少谣言传播范围。通过对比图10和图11发现WS小世界网络中谣言传播者的最大值和最终的稳定范围均大于BA无标度网络。
3 结语
本文考虑了个体兴趣度差异和辟谣机制对谣言传播的影响,并在此基础上建立了基于个体兴趣度差异和辟谣机制的IWSR谣言传播模型。计算了模型的平衡点和基本再生数R0,得出谣言消失平衡点E0全局稳定的条件,以及传播平衡点E1全局稳定和平衡点E2局部稳定的条件。理论分析与数值仿真结果表明,谣言能否得到有效传播取决于基本再生数R0的取值,当R0>1时,谣言广泛传播;当R0<1时,谣言最终消失。基于此研究结果,可得出有效抑制谣言传播的方式:政府或官方媒体加大辟谣力度以增加δ的影响力度或加强个人的防范意识、提升辨识能力以降低λi(i=1,2)的影响力等均能有效抑制谣言传播。在WS小世界网络和BA无标度网络上的仿真结果表明:1)谣言传播者达到的最大值及最终的稳定值与网络的拓扑结构有一定的关系;2)在各网络拓扑结构下,传播者数量随辟谣力度的增大而降低,且提升个体的辨识力等可有效降低谣言的影响范围。
本模型在均匀网络上研究了个体兴趣度和辟谣机制对谣言传播的影响,然而实际的社交网络是具有无尺度与小世界双重特性的复杂网络。此外仍有影响谣言传播的因素未考虑进谣言传播模型,因此下一步的工作将更全面考虑影响谣言传播的因素,建立更加适用于复杂社交网络的谣言传播模型。

