高中数学课函数奇偶性教学分析

（广州市增城区第一中学 广东广州 511300）

函数的重要性质之一便是奇偶性，函数的奇偶性在代数、几何以及高等数学中均有广泛性应用，直接影响高中生数学高考成绩，故此高中数学教师应给予《函数的奇偶性》教学工作一定重视。对于高中生而言，初学《函数的奇偶性》，可能会产生很大陌生感，无法正确理解函数的奇偶性以及其间的差别，此时就要求教师在教学工作中不断反思教学方法的可行性，精心规划，为学生打造不断掌握函数奇偶性知识的“阶梯”。

一、构建问题情景，导入新课

兴趣是最好的老师，也是求知欲的起始点，高中数学教学的终极目标是协助不同能力的学生学有所得，数学知识与水平均有不同程度的提升。在素质教育理念广泛推行的时代中，教师应积极将课堂的主动权移交至学生手中，认真钻研教材，竭尽所能创设问题情景，调动学生对数学问题思考的主观能动性，在学习数据知识过程中获得一定成就感，逐渐喜欢上这门学科[1]。在《函数的奇偶性》课堂教学中，教师的教学任务之一是将静态的、学术色彩极为浓烈的“数学文化”转型为动态式、富有教育意义的“数学文化”。

例如，为促使学生能够能正确辨识奇函数与偶函数，教师在课堂教学中采用小组合作方法去完成以上教学任务，首先教师结合学情，按照“组内有别、组间同质”的原则，将班级同学划分为不同小组；其次，采用多媒体教学技术，为学生展示了图1图像，鼓励学生以口答的方式判断函数的奇偶性。

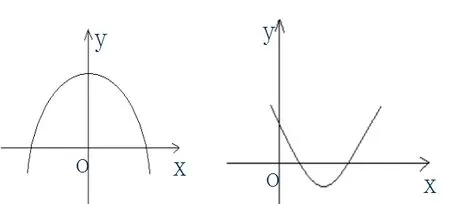
图1

再如，为促使学生能深刻掌握图像对称性，教师同样采用小组合作教学方式，为其设置“已知函数y=f(x)是偶函数，其在x轴右边的图像见图2，轻尝试画出y轴左边的图像”这一问题。采用小组合作方式以及多媒体技术教学，能够帮助学生在互相合作的情景下有效学习与应用函数奇偶性的相关知识，此外笔者认为图片导入也能给学生带来新鲜的视觉冲击感，进而集中注意力看题、做题与记忆解题方法，优化课堂教学质量的同时，为学生后续阶段学习函数知识奠定良好基础。

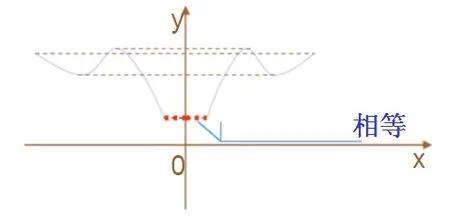
图2

二、采用任务驱动式，设计思路讲解课程

1.明确学习任务

任务驱动教学模式运行期间的侧重点是促使学生“动”起来，教师可用一个课时时间去协助学生梳理资料，鼓励学生充分的表达，但不要过度的重视学生对任务的完成情况，其宗旨是促使学生对奇函数、偶函数有初步认识[2]。此外，也可采用分工合作、应用网络资源等方式，取达成以上目标。

2.建设基本知识内容“骨架”

学生在学习一个新知识点之前，教师需明确他们现有知识的储备量，以此为基点，深入教学，并强化教学内容与学生认知规律。由于初中生的数学基础相对薄弱画，故此在知识准备方面上教师应主动挖掘，只要和目前所学知识相关联的数学知识，应冲破不同年级的局限性，积极将其融合至数学课堂教学体系中，争取让每一名学生学有所得、学有所获[3]。例如，在讲解“轴对称”知识时，教师可以采用网络查询、几何画板软件等方法，画出（1）y=x2；的函数图像。在以上教学任务中函数习题与初等函数中的幂函数以及幂函数的甲减、绝对值函数等相关，以上函数的定义域均是实数，画出图形后无需改动。

3.随堂例题和练习

《函数的奇偶性》教学中，要解决的问题可作出如下归纳：（1）对奇函数、偶函数的正确辨识；（2）明确奇偶函数的图像特点；（3）掌握奇偶函数的代数特点；（4）采用代数方法证明函数的就行。在以上教学内容中，重点是研究函数的奇偶性，研究函数的定义域是前提，在此基础上排除既不是奇函数又不是偶函数的一类函数。例如教师在课堂教学中，提供如下练习题：采用定义判断f(x)=x3+2x的奇偶性。采用定义判断函数奇偶性可参照如下流程：首先，求得定义域，判断其是否关于远点对称；其次，再判断f(-x)和f（x）之间的关系；最后，如果f(-x)=f（x），则f（x）为偶函数；如果f(-x)=-f（x），则f（x）为奇函数。

三、复习与总结，巩固知识

在判断函数奇偶性的问题中，很多学生缺乏认真严谨的态度，他们多看重的是问题表面而忽视了定义域相关问题，导致知识点掌握缺乏扎实性，故此在判断函数奇偶性问题时经常出错。总结几年教学经验，笔者认为尽管《函数的奇偶性》这一章节的知识点理解与掌握上并不存在较大难度，但是在考查知识点掌握情况时，很多学生会因为各种各样的错误而后悔不已[4]。

故此，在课堂教学中教师一定要重点强调：在判断一个函数的奇偶性时，首要步骤是辨识其定义域是否关于坐标原点O对称，即对于定义域中任意一个自变量x，它的相反数-x是否也在定义域中。列出的函数，若没有标注其定义域，那么采用怎样的方法明确其定义域？那么就要求使这个函数具有意义的实数集合，也就是该函数的定义域。

结语

数学是一门具有鲜活色彩的艺术品，一节课能否取得良好的教学效果，关键在于是否进行较高水平的思维活动，是否紧扣学科概念的本质与主要的思想方法进行，是否结合学生的认知水平设置相关问题，引导学生主动思考，培养他们的思维能力，并协助他们养成良好的学习习惯与方法。在《函数的奇偶性》课堂教学中，教师应结合学情与课程教学大纲相关内容，设计启发性问题，构建问题情景，提升学生学习知识主动性，最大限度的优化课堂教学质量。