例谈高中数学中圆与其他知识的的联系

（广东省深圳市龙岗区横岗高级中学 广东深圳 518100）

圆的方程及性质是高中数学中的核心教学内容。它经常与其他知识巧妙地结合在一起，因而，学生不容易掌握。谈到了圆在距离问题、方程根问题、不等式问题、函数最值中的应用。本文将从以下方面谈谈圆在数学解题中的应用。

一、与平面向量的联系

例1 在平面直角坐标系中，O为原点，A（－1，0），B（0，），C（3，0），动点D满足||＝1，则|＋＋|的最大值是________。

分析:本题学生的常规思路是得到|＋＋|的表达式后消元，转化为研究函数的最值问题，这样运算量颇大。而用本文的方法，可获简解。

解：设D（x，y），由||＝1，得（x－3）2＋y2＝1，

向量＋＋＝（x－1，y＋），

故|＋＋|＝的最大值为圆（x－3）2＋y2＝1上的动点到点（1，－）距离的最大值，其最大值为圆（x－3）2＋y2＝1的圆心（3，0）到点（1，－）的距离加上圆的半径，即＋1＝1＋。

点评：函数的最值问题通常用代数办法解决，但如果函数的表达式与圆的方程类似时，则数形结合的方法会相对简单。

二、与线性规划问题的联系

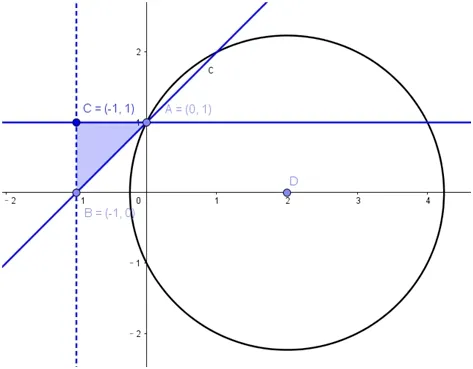
解法2：由约束条件画出可行域，如下图。

三、与复数的联系

例3 若复数z满足的最大值和最小值。

分析：本题用代数方法计算，运算量很大。可考虑用数形结合的方法，而的轨迹是一个圆形区域。

设复数z对应点为A，复数对应的点为

复数z对应的点在复平面上的轨迹是以点M为圆心，1为半径的圆形区域，如图，

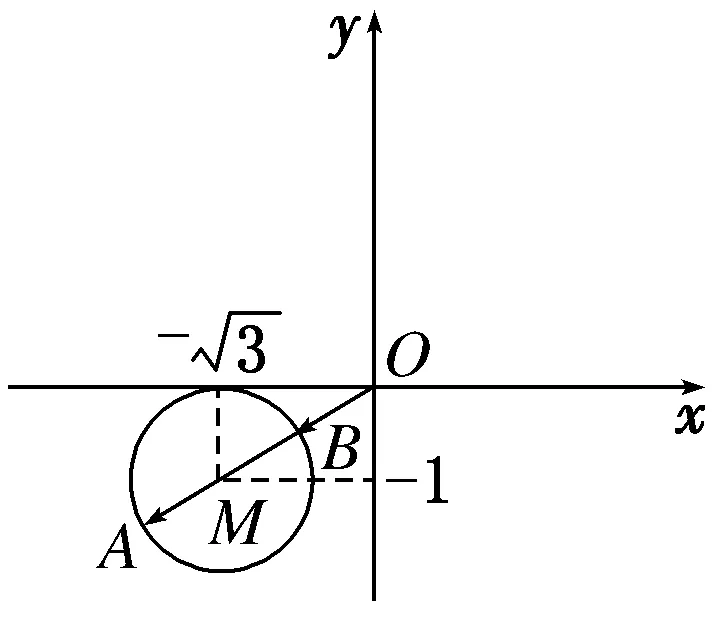
根据圆的几何性质知，动点A到原点O的距离最大值为2+r=2+1=3，最小值为2-1=1，

点评：若复数z满足则z对应的点的轨迹是圆。通常涉及复数的模问题，可与圆联系，利用数形结合的方法。

四、与定积分求值的联系

解：由定积分的几何意义知，所求定积分是由x＝0，x＝2，y＝，以及x轴围成的图象的面积，即圆（x－1）2＋y2＝1的面积的一半，∴。

点评：当f(x)的原函数不容易求出时，可考虑定积分的几何意义。