关注学习心理，提升思维品质——中考数学二轮复习的教学策略

☉江苏省江阴市第一初级中学许建云

中考复习课是广大一线教师非常关注的课型，在众多数学教育工作者的共同探究下，对中考复习已经形成了诸多的共识，如进行三轮中考复习、每轮复习的教学目标、课堂教学的组织形式等.但是对于中考复习课的组织实施，每轮教学目标的达成策略，学生复习课的学习心理，仍然缺乏理论的指导和系统的研究，特别是很多老师认为二轮复习是“鸡肋”从而可有可无，因为一轮复习时归纳和整理三年所学的内容已经花费了大量的时间，又要急于进行三轮模拟训练，很多教师在二轮复习时都是跟着经验走，却缺少针对性，复习效果不佳.笔者于2017—2018学年度在初三年级任教，从教学实践来看，二轮复习是提高综合能力最重要不可或缺的环节之一，起到承前启后的作用.本文试图对二轮复习的教学策略进行阐述，以期引起同行的探讨.

一、教学目标分析

一轮复习以知识梳理和系统建构知识框架为主，提高基础知识记忆的持久性，增强运用基础知识和基本方法解决问题的灵活性.二轮复习应该突出重点，研究本地区中考的特点和亮点，围绕数学思想方法，以专题复习的方式展开教学，增强学生解决综合性问题的能力.如果说一轮复习是纵向的，那么二轮复习就是横向的.教学的目标应该是把数学思想方法和解决问题的策略由内隐转向外显，加深对数学知识和方法的理解，建构学生自己程序化的知识系统和解决问题的方法系统，为三轮的综合训练打下坚实的基础.

二、学情分析

通过第一轮的复习，学生对初中所学的知识有了较为系统的认识，大多数学生的基础知识、基本技能都得到进一步巩固，能够做到基本技能程序化、熟练化，知识的记忆更加持久，知识的提取更加迅捷；对数学思想方法的认识也更加深刻，逐步呈现由内隐向外显变化的趋势，但是还没有形成自觉的意识，还没有达到自动化的程度，对于隐含在问题中的数学思想方法运用得还不够熟练；同时积累较多的探索和解决问题的经验，解决问题的策略表现为模糊的类化，对数学知识和方法的认知还有待进一步提高.

三、学习心理分析

二轮复习以横向为主，突出重点和考试的热点，特别是重要的数学思想方法和解决问题的策略为教学的主要目标.从学习心理的角度来看，数学思想方法和解决问题的策略都是程序性知识，认知心理学认为：程序性知识学习的本质是掌握一个程序，即在长时记忆中形成一个解决问题的产生式系统.以后若遇到同样类型的问题，就可以按照这一产生式系统的程序，一步一步做下去，直至解决问题.基于上述学习的心理学基础，二轮复习时，应该根据新课程标准的要求，加之本地区中考的热点问题，选择最为合适的专题进行教学.笔者认为，初中阶段最适合研究的专题有：分类讨论专题、数形结合专题、图形运动变化专题、实际问题专题、函数与方程思想专题、尺规作图与网格画图专题等.

四、教学策略探究

依据专题复习的学习心理，二轮复习课的教学可以分为四个环节进行：

教学环节1：问题情境

二轮复习要达成前述目标，选题是非常重要的环节.在课堂上要给学生呈现最典型的情境，以问题为驱动和抓手，深化对数学思想方法的认识，对解题策略进行概括和提炼，问题的选择应该是教学中的重点问题，考试中的热点问题，学生掌握中的棘手问题，以期使教学更有针对性和时效性.以下是笔者在中考二轮复习时研讨课部分实录和笔者的思考：

问题：（2014年铁岭改编）如图1，在▱ABCD中，∠ABC和∠BCD的平分线交于AD边上的一点E，若________，则AB的长是_______.（请补充条件，设计成能求AB长度的问题）

图1

教学环节2：探究深化

学生先独立思考.

生1：若AE=1，则AB=1.由基本图形角平分线加平行线可得等腰三角形，则AB=AE.

生2：若BC=2，则AB=1.由生1的基本图形同样可得三角形CDE是等腰三角形，则CD=DE.又AB=CD，所以AB=CD=AE=DE，即BC=2AB.

师：生2有了重大发现：点E是AD的中点，这是非常不错的.还有其他的想法吗？

生3：若BE=4，CE=3，则AB=2.5.我也发现了基本图形，两平行线构成同旁内角，角平分线互相垂直.由AB∥CD，得∠ABC+∠BCD=180°.又由∠ABC和∠BCD的平分线，则∠BEC=90°.

虽然是二轮复习，仍然从低起点出发，但是问题设计是开放的，思维具有发散性和逆向性，符合二轮复习锤炼思维的目的.此题设计的另一个目的旨在引导学生运用模式识别（识别基本图形）的策略，通过结构类比进行联想、探究、猜想，寻找解决问题的途径，对以前的解题策略和方法进一步巩固、深化.

教学环节3：拓展活化

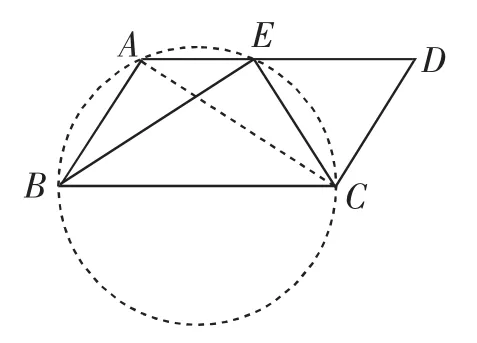
图2

学生先独立思考，后小组讨论.

变式递进：（原创）如图2，在平行四边形ABCD中，∠ABC和∠BCD的平分线交于AD边上的一点E.若以BC为直径的圆过点A，判断△CDE的形状.

师：大胆猜想：△CDE的形状是什么？然后小心求证.

生4：△CDE的形状是等边三角形.连接AC，易得∠BAC=90°.因为AB∥CD，所以∠ACD=90°.在Rt△ACD中，点E为AD的中点，所以CE=DE.由上题可得CD=DE.因此CD=DE=CE，所以△CDE是等边三角形.

生5：老师，我还有一种简单的方法.因为∠BEC=90°，可以证明点E也在以BC为直径的圆上，所以四边形ABCE为圆的内接四边形，可以得到∠ABC+∠AEC=180°.又因为∠DEC+∠AEC=180°，所以∠DEC=∠ABC.在平行四边形ABCD中，∠ABC=∠CDE，则∠DEC=∠CDE，进而得到CD=CE.再由刚才得到的CD=DE，所以CD=DE=CE，所以△CDE是等边三角形.

从认知心理学的角度来看，学生解决问题就是提取已经有的信息（即原有的知识、经验、思想、方法等），把不同的信息进行链接，链接越多，解题策略就越多，数学思想方法就越丰富，学生解决问的速度就越快，灵活性就越强.通过添加圆的元素，问题的综合性显然变强了，增加了点A经过以BC为直径的圆，“形”的条件转化为“数”的结论就是∠BAC=90°，联系前面的结论得出关键的一步CE=DE，这就是数形结合思想的充分利用，教学中要抓住这个关键，使内隐的方法外显化，让学生先探究，教师点拨，再激活学生思维，从而对数学思想方法的运用从无意识到有意识，从模糊化到清晰化、自动化.

教学环节4：感悟内化

学生自行探究，独立思考.

链接中考：（2015年无锡）已知：平面直角坐标系中，四边形OABC的顶点分别为O（0，0）、A（5，0）、B（m，2）、C（m-5，2）.

（1）是否存在这样的m，使得在边BC上总存在点P，使∠OPA=90°？若存在，求出m的取值范围；若不存在，请说明理由.

（2）当∠AOC与∠OAB的平分线的交点Q在边BC上时，求m的值.

图3

生6：由题意得OA=BC=5，BC∥OA，则四边形OABC为平行四边形.由前面的问题解决可以联想到构造辅助圆，以OA为直径作⊙D，与直线BC分别交于点E、F，则∠OEA=∠OFA=90°.如图3，作DG⊥EF于G，连接DE，则DE=OD=2.5，DG=2，EG=GF，则EG=.5，则点E（1，2）、F（4，2）.

由于时间关系，对于第（2）问，课堂上没有解决，以下附一个学生漂亮的课后解答：

解：BC=5，B、C两点在直线y=2上，直线y=2与y轴交于点G，过A点作AH⊥BC，垂足为H，如图4.

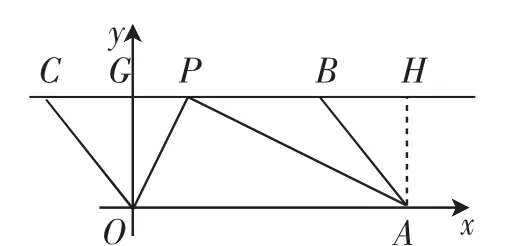
图4

（2）由BC∥OA，BC=OA=5，得四边形OABC是平行四边形.易证：∠OQA=90°，点Q在BC上，点Q为BC的中点.由（1）可得Q（1，2）或Q（4，2），则m=3.5或m=6.5.

学生从题干中发现关键条件进行充分联想，学会发现图形中隐藏的信息，引导学生发现有隐形圆的存在，让学生见直角能联想隐蔽圆，为今后遇到类似题目提供积累经验.“感悟内化”，从心理学的角度来看，其实就是将解决问题所获得的新的思想、方法与原有的“知识结构”重新进行结构化调整，形成新的知识和方法网络，这就是知识内化的过程.只有学生真正掌握了解题的策略和方法，解题时才会有很大的灵活性，思维能力才会自然得到提升.

五、教学启示和感悟

复习的专题设置要紧扣地区中考的热点和难点，从学生学习心理来看，教学过程要环环相扣，以数学思想方法的显性化和思考问题策略的自动化为目标层层递进来展开教学，教学要改变就题论题，打“题海战”的教学方法，要从数学思想方法提升和揭示数学本质的高度来组织教学.让学生在解题中学会解题，理解数学和数学思想方法，从而学会数学化地思考问题，把一轮复习中掌握的知识和方法在解题的“实战”中运用，提高学生的数学核心素养.

二轮复习是学生思维能力提升的重要一环，依据学生数学思维能力形成的心理特点，选取适当的问题，设置合理的情境，逐步让学生掌握解题方法和策略，把内隐的思想方法转变为外显的行为，形成更高级的程序化、自动化的方法链系统，实践证明，这是培养思维能力较好的途径.

参考文献：：

1.张大均.教育心理学［M］.北京：人民教育出版社，2005.F