函数周期性及其应用

■罗启明

惠州工程职业学院

函数是中学数学的主体内容，函数的周期性是函数的几个重要性质之一。对函数的周期性的是在研究三角函数的性质时给出的，对于一般函数的周期性没有进一步的介绍，因此一般函数的周期性的推导和应用成为很多学生的学习难点。本文通过对一般函数的周期性进行推导及应用，进一步培养学生严谨的逻辑思维能力和应用函数思想研究问题、讲解问题能力。

1 周期性的定义

对于函数f(x)，如果存在一个非零常数T，使得当x取定义域内的每一个值时，都有f(x+T)=f(x)，那么函数f(x)就叫周期函数。非零常数T叫做这个函数的周期。

周期函数的周期不止。如果非零常数T是一个函数的周期，那么nT(n∈Z且n≠0)都是这个函数的周期。如果在周期函数f(x)的所有周期中存在一个最小的正数，那么这个最小正数就叫f(x)的最小正周期。周期通常指的是最小正周期。

2 函数周期性判定的几个常见结论

2.1 若函数f(x)满足f(x+a)=f(x-a)，则f(x)是周期函数，周期T=2|a|。其中 a≠0。

同理可得：若函数f(x)满足f(x+a)=f(x-b)，则f(x)是周期函数，周期 T=|a+b|。其中 a≠0。

2.2 若函数f(x)满足f(x+a)=-f(x)，则f(x)是周期函数，周期T=2|a|。其中 a≠0。

2.5 若函数f(x)的图像分别关于直线x=a，x=b对称，则f(x)是周期函数，周期T=2|a-b|。其中a≠b。

推导：由条件得f(x)=f(2a-x)，f(x)=f(2b-x)，于是得f(2ax)=f(2b-x)，将上式中的x用2b-x替换后得f(2a-2b+x)=f(x)，所f(x)以周期 T=2|a-b|。其中 a≠b。

特别地，若函数f(x)是偶函数且图像关于直线x=a对称，则f(x)是周期函数，周期T=2|a|。其中a≠0。

2.6 若函数f(x)的图像分别关于点(a,0)，(b,0)对称，则f(x)是周期函数，周期T=2|a-b|。其中a≠b。

推导：由条件得f(x)=-f(2a-x)，f(x)=-f(2b-x)，于是得f(2a-x)=f(2b-x)，将上式中的x用2b-x替换后得f(2a-2b+x)=f(x)，所f(x)以周期 T=2|a-b|。其中 a≠b。

2.7 若函数f(x)的图像分别关于点(a,0)和直线x=b对称，则f(x)是周期函数，周期T=4|a-b|。其中a≠b。

推导：由条件得f(x)=-f(2a-x)，f(x)=f(2b-x)，于是得f(2a-x)=-f(2b-x)，将上式中的x用2b-x替换后得f(2a-2b+x)=-f(x)，所f(x)以周期 T=4|a-b|。其中 a≠b。

特别地，若函数f(x)是奇函数且图像关于直线x=a对称，则f(x)是周期函数，周期T=4|a|。其中a≠0。

对于5、6、7三条结论，可以利用正弦函数或余弦函数图像来进行理解和记忆。

3 函数周期性的应用举例

例1 设f(x)是R上的奇函数，满足f(x+2)=-f(x)，则f(6)=（ ）

A. -1 B. 0 C. 1 D. 2

解 析：∵f(x+2)=-f(x) ∴f(x+4)=f(x)

∴f(x)是以4为周期的周期函数∴f(6)=f(2+4)=f(2)

∵f(x+2)=-f(x)，且f(x)是R上的奇函数

∴f(2)=-f(0)=0，故选答案B

点评：

例2 若函数f(x)的最小正周期4，而f(2+x)=f(2-x)对于一切x∈R成立，则f(x)（ ）

是奇函数而非偶函数 B. 是偶函数而非奇函数

是奇函数又是偶函数 D. 不是奇函数也不是偶函数

解 析：∵T=4，且f(2+x)=f(2-x)（x∈R）

∴f(x)=f(4+x)=f(2+2+x)=f(2-2-x)=f(-x)

即 f(x)=f(-x)∴f(x)是偶函数，故选答案B

例3已知偶函数的图像关于直线x=1对称，且x∈[3,4]时，f(x)=2x-1，则x∈[14,15]时，f(x)的解析式为

解析：当x∈[-4,-3]时，-x∈[3,4] ∴f(-x)=-2x-1

又f(x)为偶函数，∴f(x)=2x-1，即x∈[-4,-3]时，f(x)=2x-1

由条件得f(-x)=f(x)及f(x)=f(2-x)，于是f(-x)=f(2-x)

∴f(x)=f(2+x)∴f(x)是以2为周期的周期函数

当x∈[14,15]时，18-x∈[-4,-3]，∴f(x-18)=-2(x-18)-1

又f(x-18)=f(x)∴x∈[14,15]时，f(x)=-2x+35

A. f(sinα)＜f(cosβ) B. f(sinα)＞f(cosβ)C. f(sinα)=f(cosβ) D. 以上答案均有可能

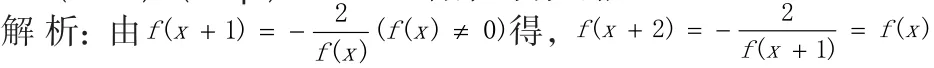
∴ 是周期为2的周期函数

∴f(2017)=f(2018-1)=f(-1)，f(2018)=f(0)

∵f(x)在区间(2017,2018)上单调递增，

∴f(x)在区间(-1,0)上单调递增。

又f(x)是偶函数，∴f(x)在区间(0,1)上单调递减

∵α,β是锐角三角形的两个内角