生成函数在递推关系问题上的应用
■崔龙飞 刘浩东
武警警官学院
1 生成函数的相关知识
1.1 生成函数的定义
母函数又叫生成函数,作为离散数学的一个重要部分的生成函数方法,其将离散数学串联沟通起连续数学,在对组合数学问题进行分析时,在组合计数方面生成函数具有天生的优越性,是对组合计数问题解决的工具。

将需要研究的数列运用幂级数或多项式合成一个整体,通过对多项式或幂级数的性质和对合并同类项的方法这个方法的使用进行研究,最终得到相关的结论,这就是生成函数的中心思想。

1.2 生成函数的基本性质
假设,序列(ak),(bk)的生成函数的分别是:
P(x)=a0+a1x1+a2x2+…Q(x)=b0+b1x1+b2x2…
生成函数和数列之间是一一对应的,因此要对两个数列之间的关系进行研究可以转化为研究它们的生成函数的关系,从而就方便解题[1]。

1.3 生成函数的计算
将相对复杂的生成函数化简成简单的二次式类型,或者是若干个二项式类型的生成函数的积,这就是计算生成函数系数的方式,从而不难得出所需要的xk的系数。要运用到牛顿二项式定理和它的生成函数的性质。
牛顿二项式定理:

举例求解生成函数:
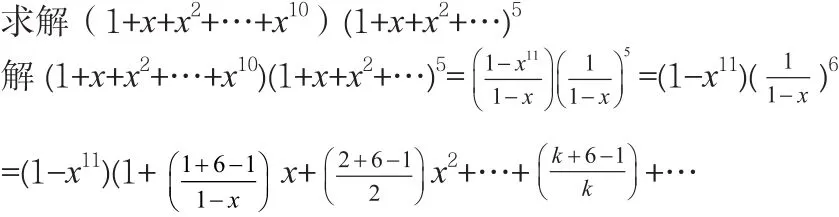
求得生成函数的系数可借助牛顿二项式定理。
数学中的递推关系问题
在数学领域中,递推关系在其有着很重要的位置和其应用也很广泛。一般情况下求解递
推关系并容易,如果只是运用递推关系的一些定义是不能解决很多问题,它关联到很广领域。
研究递推关系是追溯到斐波纳契关系:Fn+2=Fn+1+Fn,n≥0,F0=0,F1=1,最先给出的是比萨的数学家Leonardo。
数列xn必须有连续个k项满足xn+k=f(xn+k-1,xn+k-2,…,xn),满足此式的数列叫它为数列xn的一个递推关系式,这就是线性递推关系定义。
由递推关系式和满足k个初始值可以确定的一个数列xn叫做递推数列。所以,不管是设计到递推数列解析题,证明题,还是需要建立递推关系式的综合题,则求通项公式就是解决递推数列的核心,也是最基本的步骤[2]。
3 生成函数法应用于递推关系的求解
不少求排列组合计算问题的时候一般都会归结为求某个数列xn的通项公式,直接一些求数列的通项公式一般不是那么容易,然而可以求所满足的递推关系,则首选的方法就是生成函数,在求递推数列关系,一种重要的思维与常用的方法就包括生成函数。
3.1 生成函数法应用到常系数线性齐次递推关系上
定义:常系数线性齐次递推关系
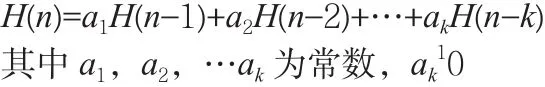
将关于an的常系数线性齐次递推关系转化为an的生成函数G(x),通常运用错位相减法,然后运用代数方法求G(x),幂级数的形式把它把展成出来,xn的系数an就是所求,这就是使用生成函数法解常系数线性齐次递推关系的基本思想。
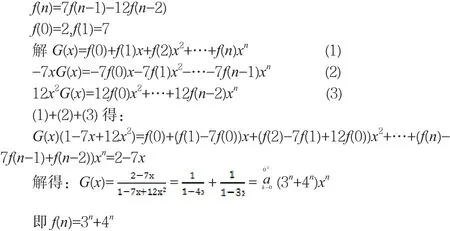
在上面例中运用到的方法,即错位相加减法,可以得知,和传统方法相比,运用生成函数的方法来求解an更加容易。
3.2 生成函数法应用在常系数线性非齐次递推关系上

使用生成函数法解常系数线性非齐次递推关系的基本思想是:设序列an的生成函数是Q(X)=anxn将关于an的常系数线性非齐次递推关系代入Q(X)=anxn的右端,得到Q(x)的方程,Q(X)的解求得出来。再用幂级数的形式把它展示出来,xn的系数an就是所求。


其中a是实数;b是常数;k是正整数。
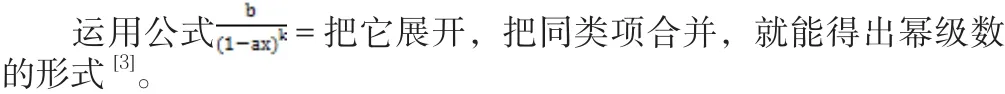
4 结语
本文通过对问题进行引入、分析、解决和延伸,对生成函数法求解常系数线性非齐次递推关系与常系数线性齐次递推关系。通过举例分析,生成函数运用到递推关系问题的求解上是很有用的,已经广泛运用到数学中。

