初中圆弧型轨迹问题解题策略

摘 要：本文通过对初中七个典型圆弧型轨迹问题的研究，发现圆弧型轨迹问题一般分为两大类，总结出了一画、二猜、三证明解题策略.

关键词：圆弧型轨迹；分类；解题策略

作者简介：袁俊峰（1976-），男，湖北荆州人，本科，中学高级教师，研究方向：试题命制与解题研究.

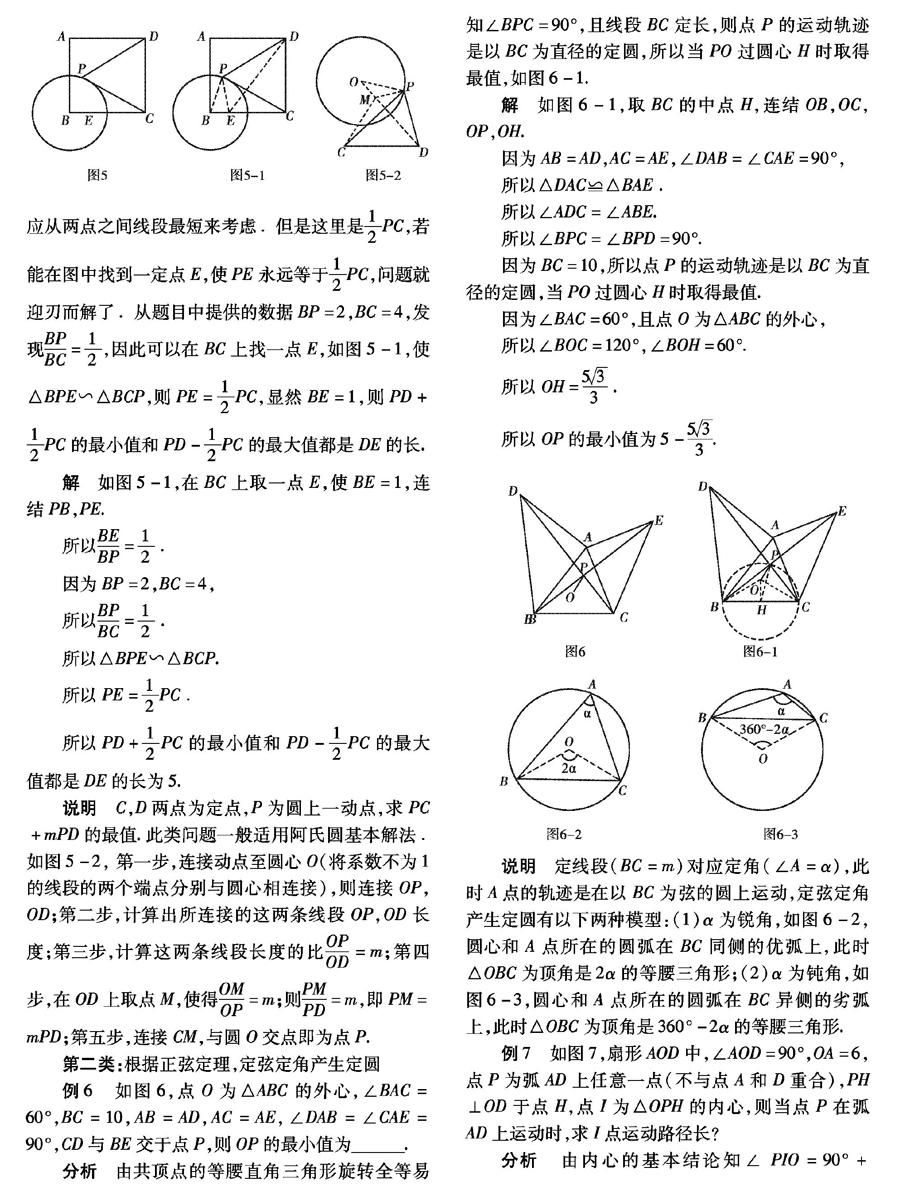
在《理科考试研究》（20189）中，我们探讨了动点轨迹问题中直线型，本文将以部分中考题为例，就如何解决圆弧型轨迹问题继续与大家一起分享 动点轨迹为圆弧的情况一般分为两大种情况：（1）到定点的距离等于定长；（2）定弦定角产生定圆 解决这类问题与直线型一样，一般可分为三个步骤：①直观感觉，画出图形，进而猜想；②特殊位置，比较结果，验证猜想；③理性分析动点过程中所维系的不变条件，通过几何构建或坐标转化，寻找动量与定量之间的关系，进一步证明猜想下面以具体实例加以说明.

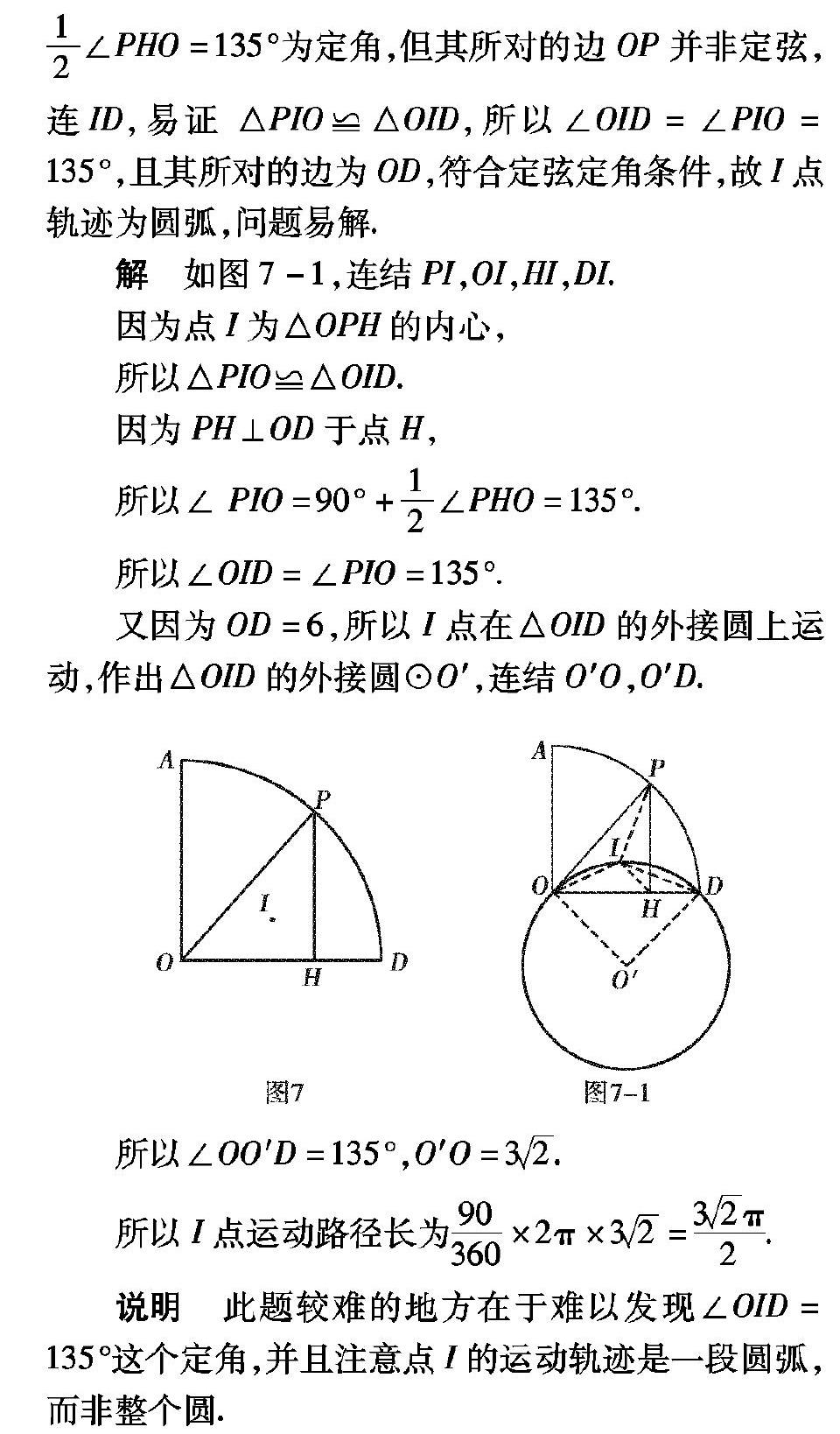
说明 此题较难的地方在于难以发现∠OID=135°这个定角，并且注意点I的运动轨迹是一段圆弧，而非整个圆.

从这两类问题的研究中还可以发现一点：若无其它限制，主动点运动路径是圆弧，从动点的运动路径也应是圆弧，并且从动点与主动点圆心角应该是相等的.面对着一个比较综合、有一定难度的数学问题，怎样才能引导学生迅速地找到其突破口，打开学生的解题思路呢？俗话说妙计可以打胜仗，良策则有利于解题，当学生对数学知识，数学思想方法的学习和运用达到一定水平时，应该把一般的思维升华到计策谋略的境界 只有掌握了一定的解题策略，才会在遇到问题时，找到问题的思考点和突破口，迅速、正确地解题.因此，在教學中要适当加强数学解题策略的指导，优化学生的思维品质，提高解题能力.

由朱华伟，钱展望所著《数学解题策略》一书中谈到：“把学数学比作吃核桃，核桃仁美味而富有营养，但要砸开才能吃到它 数学教育要研究的，是如何砸核桃吃核桃 教育数学呢，则要研究改良核桃的品种，让核桃更美味，更营养，更容易砸开吃净” 在实际的教学过程中我们发现许多问题，虽然属于不同的知识內容，但它们在方法策略上有相同或类似之处 从解题的角度来看，顺利解决一道数学问题除了必须具备扎实的学科知识基础，更重要的是要有灵活的方法策略 我们在解题的时候常常碰到这样的情况：在百思不解的时候，经过解题高手一点拔，我们的思路豁然开朗，闪电一般解决了问题 这说明我们并不是不熟悉问题涉及的知识內容，而是我们的方法策略不对，因此需要我们做教师的在平时的教学过程中多研究一些解题策略.

参考文献：

[1]徐宏涉圆最值问题归类解析[J]. 中学数学教学，2017（1）：38-40.

[2]朱华伟，钱展望著数学解题策略[M]. 北京：科学出版社，2009.