内置压电悬臂梁流致振动能量收集实验研究

张 敏，张鸿鑫，刘永臻，雷 林

(重庆交通大学 航运与船舶工程学院，重庆 400074)

0 引 言

近年来为应对全球能源危机，对周围环境的振动能量进行回收成为研究热点。利用能量回收装置可以将机械能转化为电能，常见的3种机械能-电能转换方式有：静电式(electrostatic),电磁式(electromagnetic)和压电式(piezoelectric)。压电式能量收集方法与传统的电磁式和静电式发电原理相比，具有结构简单，无电磁干扰，易于制作成各种所需尺寸和形状的优点[1]。

当流体经过钝体时，由于气动力的不稳定性，会诱发钝体发生振动，常见的流致振动有涡激振动(vortex induced vibration)、驰振(galloping)以及颤振(flutter)。

目前有众多学者对不同压电换能装置的流致振动能量收集进行了研究[2-3]，H.D.AKAYDIN等[4]对一个直径为19.8 mm的空心圆柱加单悬臂梁压电装置进行了风洞实验研究，获得最大功率为0.1 mW；ERIK MOLINO-MINERO-RE等[5]对一系列圆柱加单悬臂梁压电装置进行了水槽涡激振动能量收集实验，圆柱直径为8 mm时获得最大功率为0.31 μW；A. MEHMOOD等[6]对低雷诺数、高质量比的涡激振动压电能量收集进行了计算，获得的最大功率为10 μW；A.ABDELKEFI等[7]通过实验研究了上下游两个串联小立柱之间的距离和立柱的特征尺寸对压电装置输出电压和功率的影响；王军雷等[8]研究了外界载荷对三相耦合圆柱绕流涡激振动能量转换的影响，对能量收集装置进行了数值研究，得出了输出电压及功率的变化规律；王军雷等[9]对置于钝体后的PVDF悬臂梁进行了数值研究，研究的重点是PVDF悬臂梁的大变形流固耦合计算问题，机电耦合跟流固耦合采用了分步计算，对输出电压的进行了分析。

ZHANG M等[10]建立流-机-电耦合计算模型，对低质量阻尼比涡激振动压电能量收集进行了数值分析，得到不同电阻下的电压及功率输出，结果表明输出电压随着电阻的增大而增大，输出功率在特定来流速度和电阻时最大。

以上研究中结构大都可以简化为单自由度形式，因此其最大功率输出均对应特定流速，为了增大压电能量收集装置的工作带宽，提出一种内置压电悬臂梁式能量收集装置。由于压电片内置，可以减少对流场的干扰作用，降低流体阻尼，并且可以降低外部环境对压电材料的侵蚀，此类结构的研究鲜有报道。为研究此结构的能量收集特性，笔者首先对压电悬臂梁进行了自由衰减实验，获取主要影响参数，而后进行风洞涡激振动实验，分析装置的能量收集特性。

1 压电能量收集模型

如图1，一个双晶压电悬臂梁下端连接小质量块，上端固定于圆柱上端的内部，两根弹簧平行连接在垂直于压电臂面的平面，另一端固定在风洞内壁上。将圆筒下端用另一弹簧固定于圆筒上游的细铁丝上，使圆筒在实验过程中始终保持垂直于水平面。风洞内来流方向平行于压电片面，当风速一定时，圆柱在流体力作用下以一定的频率和振幅摆动，以带动压电臂以一定的频率和振幅振动，从而达到能量收集的目的。

图1 压电能量收集装置Fig. 1 Piezoelectric energy harvester

2 实验研究

2.1 自由振动实验

选用一双晶压电悬臂梁，压电材料为PZT-5H，压电基层为铜压电装置各参数见表1。在距离压电片200 mm处安装激光位移传感器(HG-C1200)，用于测量质量块的振幅，其输出信号由示波器(UTD2000L)显示并记录。双晶压电片采用并联方式连接负载电阻，负载电阻输出的电压也用示波器进行显示和记录。

表1 压电能量收集装置参数Table 1 Parameters of piezoelectric energy harvester

使压电悬臂梁的端部质量块初始位移保持不变，同一电阻下进行10次自由振动衰减实验，电压随时间变化曲线如图2，由示波器采集数据进行傅里叶变换，得出压电臂每一电阻下的固有频率，见图3。压电臂的固有频率随着负载电阻的增加而增加，并在电阻达到一定值后趋于稳定，固有频率的变化幅度相对较小约0.498%。

由欧姆定律可得负载电阻与电压电流之间的关系：

图2 输出电压时程曲线Fig. 2 Time-history curve of output voltage changing with time

(1)

其中负载总电阻表示为

(2)

RO为示波器的内阻，在本次实验中RO=1×107Ω。

负载电阻上瞬时消耗的功率为

(3)

交流电瞬时功率是时变函数在时间间隔[t0,t1]之间，负载电阻所消耗的功率为

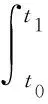
(4)

在相同的时间间隔内负载电阻消耗的平均功率为

(5)

不同电阻下初始电压如图4，随着负载电阻的增加，电压输出值也在增大。

每种阻值的电阻消耗的平均功率如图5，时间间隔[t0,t1]取[0,1.5]。R=134 175 Ω时输出最大功率，这时压电悬臂梁的阻尼也达到最大值，见图3。

建立单自由度机电耦合模型，用以评估负载电阻对压电臂固有频率及阻尼的影响[11]，该模型表示如式(6)、式(7)：

(6)

(7)

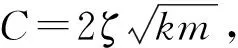
图4 不同阻值下初始电压值Fig. 4 The initial voltage of different resistance

图5 不同阻值下输出的平均功率Fig. 5 The average power of different resistance

机电耦合系数即是指压电振子在振动过程中，将机械能转变为电能，或将电能转变为机械能，这种表示能量相互变换的程度。它可以由式(8)确定：

(8)

式中：foc=7.828为压电臂开路时(R=5×106Ω)的固有频率，fsc=7.789为压电臂短路时(R=6 745 Ω)的固有频率。得出θ=1.22×10-4N/V。

对式(6)、式(7)进行线性分析，设

(9)

则上式(9)对时间的一阶导数可表示为

(10)

以矩阵形式表示为

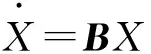
(11)

(12)

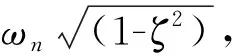
从图3中可以看出，数值计算的阻尼比和频率响应曲线与实验值相吻合。

2.2 风洞实验

将压电悬臂梁一端固定于圆筒内部，弹簧两端固定于风洞内壁，风洞空气是由一台370 W的电机带动轴流风机驱动，由一个400 W的变速器实现无极调速，风速变化范围为2～13 m/s。测试段剖面为(190×190)mm2，长度为783 mm，压电装置置于测试段的中后部。在风洞外距圆筒200 mm处安装激光位移传感器，用于测量圆筒的在垂直于压电片平面的振幅，由自由振动实验测得圆筒的固有频率fc=2.895。激光位移传感器的输出信号以及压电片输出电压均由示波器同步显示和记录。主要实验装置及安装情况如图6。选用106Ω电阻进行实验，风速范围为2～13 m/s。

图6 实验装置布置Fig. 6 Experimental setup

2.3 实验结论

如图7，图8，随着风速的增加，圆筒和压电悬臂梁的振幅逐渐增大，输出电压也逐渐增大，风速U=11.8 m/s时，电压和振幅达到最大值，Vmax=3.391 V，Amax=7.66 mm。

如图9，随着风速的增加，压电悬臂梁和圆筒的频率有着较小的变化，其变化趋势基本一致，这表明压电臂由于外部圆筒的振动而作受迫振动。

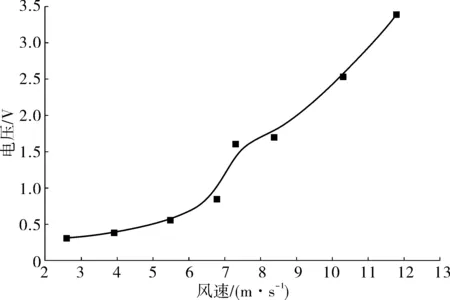
图7 不同风速下输出电压响应曲线Fig. 7 The response curves of the voltage for different wind speed

图8 不同风速下圆筒的振幅Fig. 8 The amplitude of cylinder for different wind speed

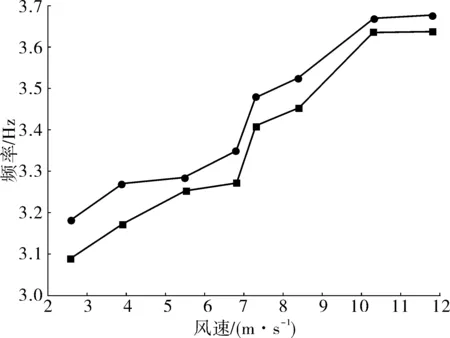
图9 不同风速下压电片和圆筒频率Fig. 9 The frequency of piezoelectric sheet and cylinder for different wind speed

3 结 语

压电能量收集是自然界能量收集的一种重要形式，因此如何提高压电能量收集器的工作带宽和性能问题是非常重要的。

首先对压电悬臂梁进行自由振动衰减实验，确定了压电悬臂梁在不同负载电阻下的固有频率和阻尼。在不同的负载电阻下压电片的固有频率有微小变化，这是由于分流阻尼效应产生的。利用开路与短路的固有频率，确定了压电片的机电耦合系数。

风洞实验表明，随着风速的增大，圆筒的振幅和频率也随之增加；通过圆筒与压电悬臂梁振动频率的对比，表明整个过程中压电臂受圆筒振动激励做受迫振动，其输出电压也随着风速的增大而增大。研究结果表明该能量收集装置能有效的采集能量，在风速U=11.8 m/s时电压值达到了3.391 V左右，在R=137 175时输出功率达到最大，约为0.173 mW。