悬索桥锈蚀主缆钢丝力学性能退化研究

韩依璇，辛付开，张国荣，朱晓文

(1. 苏交科集团股份有限公司，江苏 南京 211112； 2. 在役长大桥梁安全与健康国家重点实验室，江苏 南京 211112；3. 河海大学 力学与材料学院，江苏 南京 210098)

0 引 言

悬索桥具有跨越能力大、受力性能良好、桥型美观等特点，在桥梁建设中得到广泛应用，成为特大跨径桥梁的首选[1]。然而在运营期间，悬索桥主缆长期受到动荷载和复杂环境的耦合作用，在几年甚至十几年时间就会出现力学性能退化的现象。因此，掌握实桥主缆钢丝力学性能退化对悬索桥主缆强度评估具有重要的基础意义。悬索桥主缆承载能力的降低受腐蚀、断丝以及次应力的影响[2-4]。腐蚀是影响高强度钢丝性能退化的主要原因之一[5-6]。迄今为止，国内外学者对腐蚀钢丝力学性能退化进行了若干研究。

在锈蚀钢丝拉伸性能方面，R.BETTI等[7-8]对人工锈蚀镀锌和非镀锌钢丝进行拉伸试验，认为蚀坑是降低钢丝延性的主要因素，同时建立了均匀腐蚀和点蚀钢丝的有限元模型，发现钢丝承载力下降的主要原因是由于腐蚀导致钢丝截面积的减少。S.I.NAKAMURA等[9-10]和李翠娟等[11]分别对不同腐蚀等级的钢丝进行试验，得到了受腐蚀钢丝实际抗拉强度并未降低，而钢丝伸长率却大幅度降低的结论。P.ROFFEY[12]和C.A.CLACK等[13]分别对Forth公路大桥主缆钢丝试样进行了拉伸试验，得出了主缆钢丝极限抗拉强度随着锈蚀程度增加而减小的结论。S.C.BARTON等[14]通过人工模拟加速腐蚀钢丝得到了在不同质量损失率下，其极限承载力大幅度下降的规律，并由此推断蚀坑的存在对钢丝力学性能影响远大于均匀腐蚀所造成的影响。徐俊等[15-16]对石门大桥拉索进行了试验，提出了钢丝力学性能随锈蚀程度变化的规律，并认为锈蚀钢丝拉伸性能是由蚀坑形状及钢丝净截面积所决定的。乔燕等[17]对袁州大桥腐蚀吊杆钢丝进行拉伸试验，发现随着腐蚀程度增加，延伸率与名义极限强度折减程度最大。徐阳等[18]研究了某服役斜拉桥拉索的力学性能退化状态，发现锈蚀降低了钢丝的极限应变与强度。K.SUZUMURA等[19]和S.I.NAKAMURA等[20]分别用人工刻痕研究了4种点蚀形状对钢丝拉伸性能影响，均认为蚀坑部位应力集中是其延性下降的主要原因。王磊等[21]、李富民等[22]和辛付开等[23]分别通过人工加速腐蚀试验研究了锈蚀对钢绞线力学性能影响，并根据试验建立了基于锈蚀率的钢绞线本构关系模型。

目前这些学者们的研究几乎都是对新钢丝进行加速腐蚀试验，未考虑应力历史对钢丝力学性能的影响，无法真实反映荷载与环境耦合作用下钢丝性能的劣化发展情况。另外相比斜拉索和吊杆，主缆处于更加复杂的环境下，且目前国内几乎没有基于在役悬索桥平行钢丝主缆的研究。鉴此，笔者通过对某服役多年的悬索桥主缆钢丝进行拉伸试验，研究锈蚀对主缆钢丝力学性能影响，并分析对照不同锈蚀程度钢丝各项力学性能参数的变化，并在此基础上建立锈蚀钢丝本构关系模型。

1 服役悬索桥主缆钢丝状况

该在役悬索桥主缆由19束91根Φ5高强镀锌平行钢丝索股组成，直径为240 mm，钢丝标准强度为1 670 MPa，主缆服役时间约18a，图1为该悬索桥主缆腐蚀情况。

图1 悬索桥主缆腐蚀状况Fig. 1 Corrosion state of main cable of suspension bridge

从拆除主缆钢丝中，笔者截取了腐蚀严重位置处长约1.8 m的全截面钢丝，即19股共计1 729根主缆钢丝进行检查。参考国外楔开方法及该悬索桥主缆19股钢丝束的排列方式，沿主缆截面30°、60°为间隔进行楔开，分为8个楔开区域。室内根据钢丝锈蚀状态记录钢丝最小直径Dmin即蚀坑最深处的钢丝直径，并建立腐蚀截面图，如图2。由图2可知：钢丝最小直径从内部至外部逐渐减小，最小直径为4.70～4.85 mm的钢丝占了钢丝总数的57%。

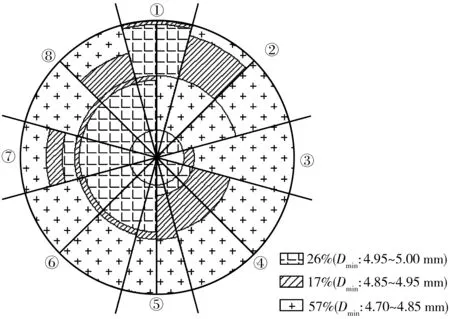
图2 主缆腐蚀截面Fig. 2 Corrosion cross-section of main cable

19股钢丝均匀的取钢丝样本，其长度为40 cm，共截取40根锈蚀钢丝，并对上述钢丝样本进行除锈，如图3为钢丝样本原状和经砂纸打磨机械除锈后的外观；然后用精度0.01 mm的游标卡尺和单尖头千分尺测量蚀坑参数。

图3 钢丝除锈Fig. 3 Steel wire derusting

2 钢丝锈蚀程度评估

当前评价钢筋和钢丝锈蚀一般采取两类指标：①一种是忽略局部腐蚀，通过质量损失或平均直径来评价，如钢丝均匀腐蚀深度、质量损失率ηρ；②另一种是根据局部腐蚀，通过蚀坑处截面面积或直径来评定，如最小直径Dmin。两类指标的计算分别如式(1)：

(1)

式中：ηρ为质量损失率；m0为原始钢丝质量；m为钢丝除锈后质量；α为最深蚀坑与直径之比；D为原钢丝直径；Dmin为钢丝最小直径。

主缆钢丝锈蚀是复杂的过程，一般而言点蚀与均匀腐蚀同时存在，故上述锈蚀程度指标过于局限。因此，笔者参考钢筋锈蚀率，提出基于最小截面积损失率ηs钢丝锈蚀评估指标。通过对蚀坑统计可知，蚀坑大都是半球形，因此针对半球形蚀坑定义了最小截面积损失率，如式(2)：

(2)

式中：ηs为最小截面积损失率；A为原钢丝截面积；Asc,ave为因均匀腐蚀所减少的截面积；Asc,min为因蚀坑所减少的截面积。

3 钢丝拉伸试验及分析

3.1 拉伸试验

按照文献[24]、[25]规定，笔者采用Instron HDX系列大载荷液压万能材料试验机进行拉伸试验，测定钢丝强度、延伸率等力学指标参数，其中屈服点取为残余应变为0.2%时的数据，试验加载控制位移为0.06 mm/s。

拉伸试验中钢丝样本长度为40 cm，标距为250 mm。图4为钢丝墩头处理及应变片布置。为防止钢丝在拉伸过程中出现滑移现象，对钢丝端头进行墩头处理，并在此基础上预加螺帽使墩头受力均匀，同时为测定钢丝应变，在标距范围内等间距布置LD20纵向应变片。

图4 钢丝处理及应变片布置Fig. 4 Steel wire treatment and strain gauge layout

3.2 拉伸试验结果分析

通过对40根服役主缆钢丝和10根新钢丝进行拉伸试验，分别选择具有代表性的5根服役主缆钢丝和1根新钢丝得到了两类锈蚀程度评价指标的应力-应变曲线(图5)，1代表新钢丝的应力-应变曲线，2～6代表不同锈蚀程度的服役主缆钢丝。图5中所对应强度均为名义强度，即荷载/未锈蚀面积。

从图5可发现：①在不同锈蚀程度评价指标下，随着锈蚀程度增加，钢丝名义极限强度、名义屈服强度和延伸率均有明显下降趋势；②延伸率减小远大于这3种锈蚀程度指标的减小，锈蚀严重降低了应力-应变曲线的强化阶段；③主缆钢丝同时存在均匀腐蚀和蚀坑，在考虑局部腐蚀评价指标下，钢丝在不同ηs和α的应力-应变曲线发生明显变化，对ηs和α比较敏感；然而对只考虑均匀腐蚀的ηρ却不敏感，曲线变化不明显。

综上所述，笔者采用最小截面积损失率ηs来评价钢丝腐蚀程度。图6为最小截面积损失率与最深蚀坑和直径之比存在线性关系，利用该转换关系对不同锈蚀指标进行换算，拟合公式为ηs=0.58α。

图6 不同锈蚀程度指标之间的关系Fig. 6 Relationship between different corrosion degree indexes

3.3 断口形貌分析

对经过拉伸试验的40根锈蚀钢丝样本，通过观察其断口形貌，可发现当ηs<1%时，钢丝断口大都为杯锥式断口；当ηs>1%时，钢丝断口大都为劈裂-铣刀式断口。

当钢丝腐蚀程度较轻，其ηs=0.6%时，最小直径Dmin=4.96 mm，钢丝在拉伸试验断裂前出现明显颈缩，断口呈杯锥式，属于宏观延性断口，如图7(a)。

随着最小截面积损失率增加，当ηs=1.36%、3.06%时，即最小直径Dmin=4.86、4.70 mm，钢丝在拉伸断裂前未出现颈缩现象，断口呈劈裂-铣刀式断口，断口处有蚀坑的存在，很明显是宏观脆性断口，如图7(b)、(c)。

图7 钢丝断口形貌Fig. 7 Fracture surface of steel wires

4 力学性能退化规律及模型

当前计算锈蚀钢丝的极限强度βuz基本有3种方法：① 蚀坑极限强度βu1，即钢丝荷载与锈蚀钢丝最小截面之比；② 平均极限强度βu2，即钢丝荷载与锈蚀钢丝平均截面积之比；③ 名义极限强度βu3，即钢丝荷载与未锈蚀钢丝截面积之比。

如图8分别为钢丝极限强度、屈服强度、延伸率、极限应变及弹性模量的相对值变化规律，分别为βu、βy、βδ、βεu、βE。通过拟合得到最小截面积损失率与各力学性能参数之间的关系，拟合相关系数均大于0.9，相应锈蚀钢丝力学性能退化如式(3)：

(3)

式中：fuc、fyc、δsc、εuc、Esc分别为蚀坑极限强度、蚀坑屈服强度、延伸率、极限应变、弹性模量；fu、fy、δs、εu、Es分别为新钢丝实际极限强度、屈服强度、延伸率、极限应变以及弹性模量。

由图8可知：服役18年的钢丝随最小截面积损失率ηs的增加，其蚀坑极限强度、蚀坑屈服强度、极限应变以及伸长率逐渐降低，而弹性模量基本不变；其中强度变化较小，而延伸率及极限应变变化很大且退化趋势相似，说明锈蚀严重影响钢丝延性并且削弱了其截面面积。主要原因是由于蚀坑存在，会引起复杂空间应力分布和局部应力集中，从而导致钢丝的延性退化，出现脆性断裂现象。

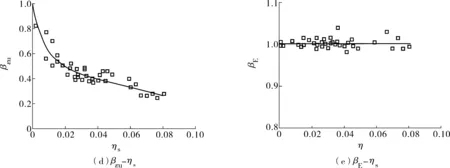
图8 锈蚀钢丝力学性能退化规律Fig. 8 Degradation law of mechanical properties of corroded steel wires

图8(a)中：与名义极限强度βu3、均匀极限强度βu2相比，蚀坑极限强度βu1随着ηs的增大，其下降速度更缓，是因为名义极限强度和均匀极限强度分别对应的是未锈蚀钢丝截面积、平均截面积。前者未考虑锈蚀导致的钢丝截面减小，后者虽考虑了均匀腐蚀和点蚀造成的钢丝截面减小，但与蚀坑极限强度相比，均匀极限强度所对应的因点蚀造成钢丝截面的减小被换算成了平均截面积，并未考虑到蚀坑形貌及其实际截面大小。

为进一步对比上述模型实用性，笔者借鉴了R.BETTI等[7]、陈先亮[26]和徐俊[27]分别对拉索及吊杆钢丝的拉伸试验数据，根据最小截面积损失率与最深蚀坑和直径之比转换关系得到了相应最小截面积损失率，通过数值拟合得到了强度退化模型，并与文中退化模型进行对比。

图9分别为蚀坑极限强度、蚀坑屈服强度和极限应变退化模型的对比，具体退化公式见表1。

由图9和表1可知：文中的蚀坑极限强度、极限应变退化模型与陈先亮[26]和徐俊[27]所得出的退化规律基本相同；但是与R.BETTI等[7]得出的极限应变退化模型差别交大，不过其退化趋势相似，究其原因是R.BETTI等[7]采用人工加速腐蚀的钢丝试样更接近均匀腐蚀，与实桥钢丝锈蚀状况不同，造成了对钢丝力学性能指标参数退化程度评估较低。

5 锈蚀钢丝本构关系模型

当前钢丝本构关系模型为双折线和多折线模型，根据上述锈蚀钢丝退化模型，笔者以双折线模型为基础，提出了包含最小截面积损失率的锈蚀钢丝本构关系模型，如图10。

图10中：双折线模型的fyc、fuc、Esc可由式(3)确定，屈服应变可由式(4)确定：

(4)

图10 锈蚀钢丝本构关系模型Fig. 10 Constitutive relation model for the corroded steel wires

根据双折线本构关系模型及力学性能退化公式(3)、(4)，可得到最小截面损失率ηs<10%时的锈蚀钢丝本构关系模型，如式(5)：

(5)

笔者根据上述公式对最小截面积损失率ηs分别为1.14%、2.36%、3.28%、4.48%、9.02%做出了对应锈蚀钢丝本构关系模型，并与相应拉伸试验曲线结果进行对比。图11即为锈蚀钢丝本构关系模型和拉伸试验曲线对比，可发现该模型与锈蚀钢丝的拉伸曲线结果较符。

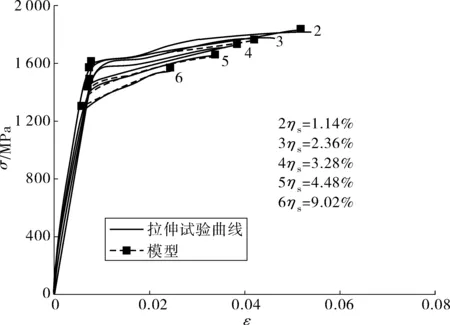
图11 锈蚀钢丝本构关系模型与试验曲线对比Fig. 11 Comparison between constitutive relation model and testing curves for the corroded steel wires

6 结 论

笔者对某悬索桥上取得的主缆钢丝样品进行拉伸试验，分析了服役了18年的悬索桥主缆钢丝力学性能退化规律，得到如下结论：

1)对在真实环境下服役的锈蚀主缆钢丝，均匀锈蚀和蚀坑同时存在，笔者采用最小截面积损失率来评价钢丝锈蚀程度更准确、方便。

2)随着锈蚀程度增加，发现锈蚀钢丝弹性模量基本无变化，而极限强度、屈服强度、极限应变以及延伸率呈现降低趋势。其中延伸率下降最快，蚀坑存在是导致延性下降的主要原因。

3)对钢丝拉伸断口形貌进行分析，发现随着锈蚀程度增加，断口形貌由延性断裂变成脆性断裂，颈缩现象也随之消失。

4)基于试验结果，得到了锈蚀钢丝蚀坑强度、伸长率、极限应变以及弹性模量与最小截面积损失率之间的定量关系模型。建立了当ηs<10%时的锈蚀钢丝本构关系模型，然而对腐蚀程度更严重的钢丝退化模型有待于对更多实桥钢丝进行试验分析后来补充完善。

5)根据主缆腐蚀截面图和钢丝力学性能退化模型，可得到每根主缆钢丝力学性能状况，而对主缆强度有待进一步研究。