减震措施及行波效应对千米级斜拉桥地震响应的影响

唐 双 林

(中铁十一局集团第五工程有限公司, 重庆 400037)

0 引 言

斜拉桥是我国大跨径桥梁中最流行的桥型之一，主跨1 104 m的俄罗斯岛桥大桥是目前世界上跨径最大的公路斜拉桥，主跨1 018 m的香港昂船洲大桥是目前世界上跨径最大的公铁两用斜拉桥。在未来跨越大江、大河及跨越海峡的桥梁工程中，主跨千米级的斜拉桥设计方案也具有相当的竞争力。

大跨斜拉桥设计中，较为常用的纵桥向结构体系有漂浮体系、塔-梁固结体系和漂浮体系与纵向约束装置的组合体系[1]。对于主跨超过千米的斜拉桥，采用塔、梁固结体系时，温度变化会在主梁和主塔结构中引起较大幅度的内力变化；此外，由于结构的纵桥向刚度较大，地震下主塔结构的内力响应较大。因此，千米级斜拉桥采用这种结构体系并不经济、合理。采用漂浮体系，虽然地震下主塔的内力响应较小，但主梁梁端、塔顶的位移响应较大。为了改善漂浮体系的静、动力性能，需要在塔、梁之间设置纵向约束装置，构成漂浮体系与纵向约束装置的组合体系。

谢群华[2]通过研究非线性黏滞阻尼器对东海大桥抗震性能的影响发现，通过选择适当的布置位置和黏滞阻尼器的参数可以有效降低结构在地震作用下关键部位的相对位移,同时也改善了结构构件的地震力。此外，还避免或减轻了相邻构件可能发生的碰撞以及碰撞引起的构件局部损坏。叶爱君等[3]通过工程实例分析发现，对于千米级斜拉桥只要合理选取参数，在塔、梁间设置弹性连接装置或阻尼器均能有效地控制梁端的地震位移，但阻尼器的效果更为理想。

对于大跨桥梁结构，地震波到达相邻墩、塔间的时间间隔较长，结构抗震分析中行波效应问题不可忽视。范立础等[4]对一座漂浮体系的斜拉桥的研究发现，与一致输入下的结构相比，考虑行波效应可使结构响应值产生40%的差异。

笔者以一座主跨1 500 m的斜拉桥设计方案为工程背景，对斜拉桥结构采用3种不同的塔、梁纵向约束方式，采用一致激励和考虑行波效应的非一致激励两种地震动输入方式，研究减震措施和行波效应对千米级斜拉桥结构地震响应的影响规律。

1 设计方案及分析模型介绍

设计方案为主跨1 500 m的双塔双索面钢箱梁斜拉桥，立面布置如图1。边跨处设有2个辅助墩，桥梁分跨布置为：138+138+412+1500+412+138+ 138=2 876 m，主梁为扁平钢箱梁，梁高5.0 m，梁宽41 m(含风嘴)，采用正交异性钢桥面板。每个主塔两侧均布置47对斜拉索，靠近梁端处的17对斜拉索在主梁上的间距均为12 m，其余部分斜拉索在主梁上的间距均为16 m。主塔为高370 m的混凝土倒Y型桥塔，基础为采用钻孔灌注桩的高桩承台群桩基础。

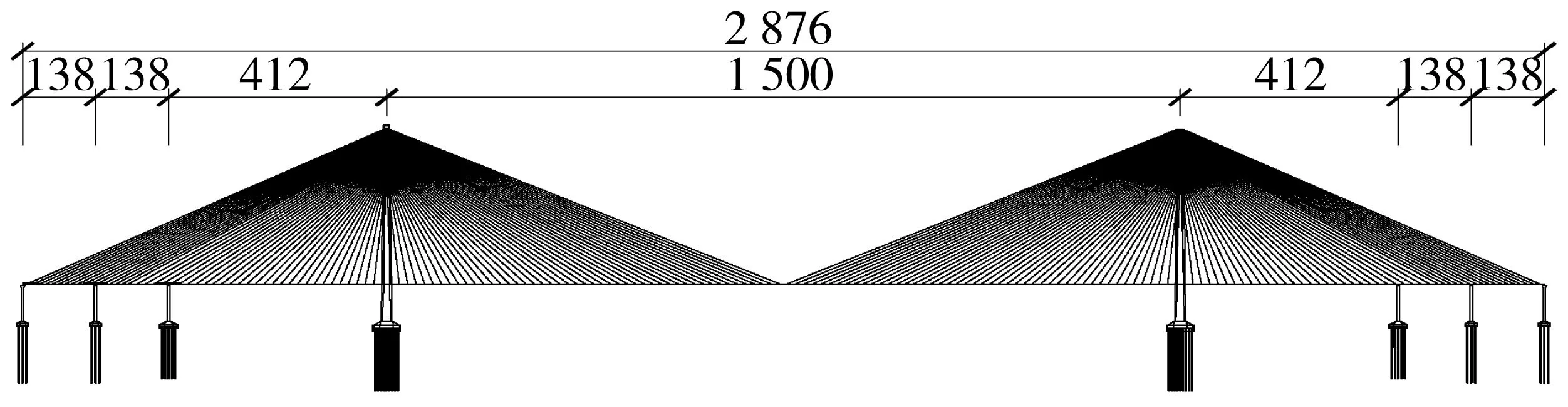
图1 主桥立面布置(单位:m)Fig. 1 Layout of main bridge facade

采用SAP2000建立了有限元动力分析模型，如图2。分析模型中坐标系的定义如下：纵桥向为X轴，横桥向为Y轴，竖向为Z轴。其中主塔、主梁、桥墩均采用空间梁单元模拟，非线性流体黏滞阻尼器和弹性索均用连接单元模拟。主梁采用单梁式力学模型，并通过主从约束同双索面相连；斜拉索采用空间桁架单元，采用Ernst公式修正拉索弹性模量，从而考虑拉索的垂度效应，拉索与主梁及主塔均采用刚体限制连接。在承台质心节点采用集中质量模拟承台的作用，该点与塔底或墩底节点及承台底节点采用刚体限制连接。在承台底部采用六弹簧模型模拟主桥群桩基础，以考虑桩-土相互作用。在进行模态分析时，边墩、主塔与主梁之间的连接条件如表1。

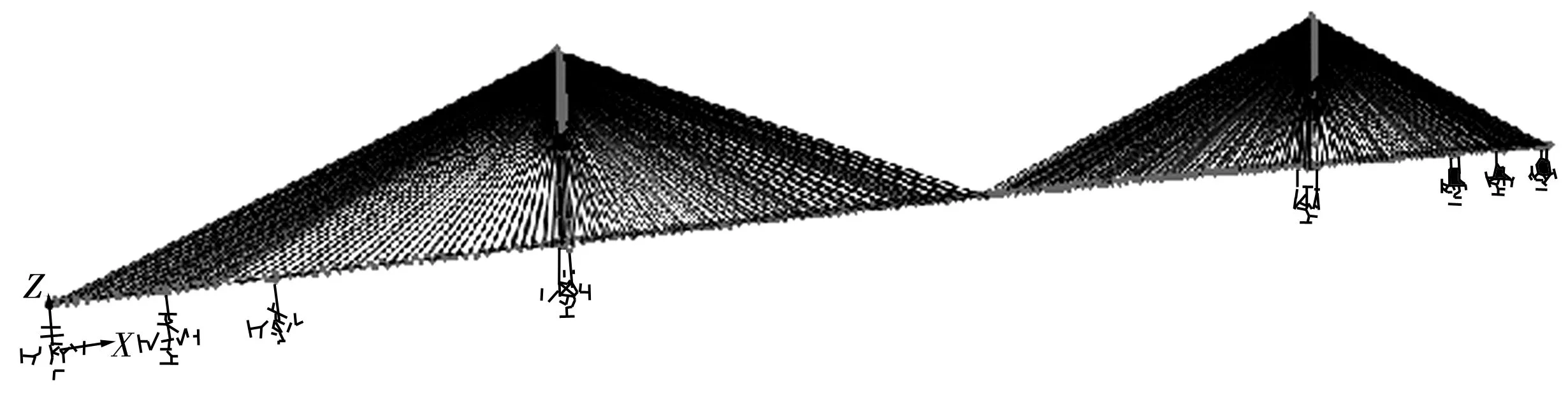
图2 主桥有限元模型Fig. 2 The finite element model of the main bridge

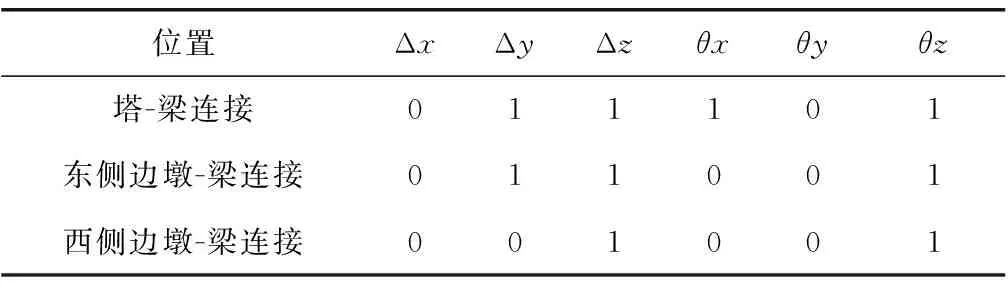
位置ΔxΔyΔzθxθyθz塔-梁连接011101东侧边墩-梁连接011001西侧边墩-梁连接001001

注：“0”表示无约束，“1”表示约束；“Δx”、“Δy”、“Δz”分别表示沿x、y、z轴方向的线位移，“θx”、“θy”、“θz” 分别表示绕x、y、z轴方向的转角。

对图2所示的主桥有限元模型进行了模态分析，表2中列出了主桥的前5阶振型的形状及特征周期值。

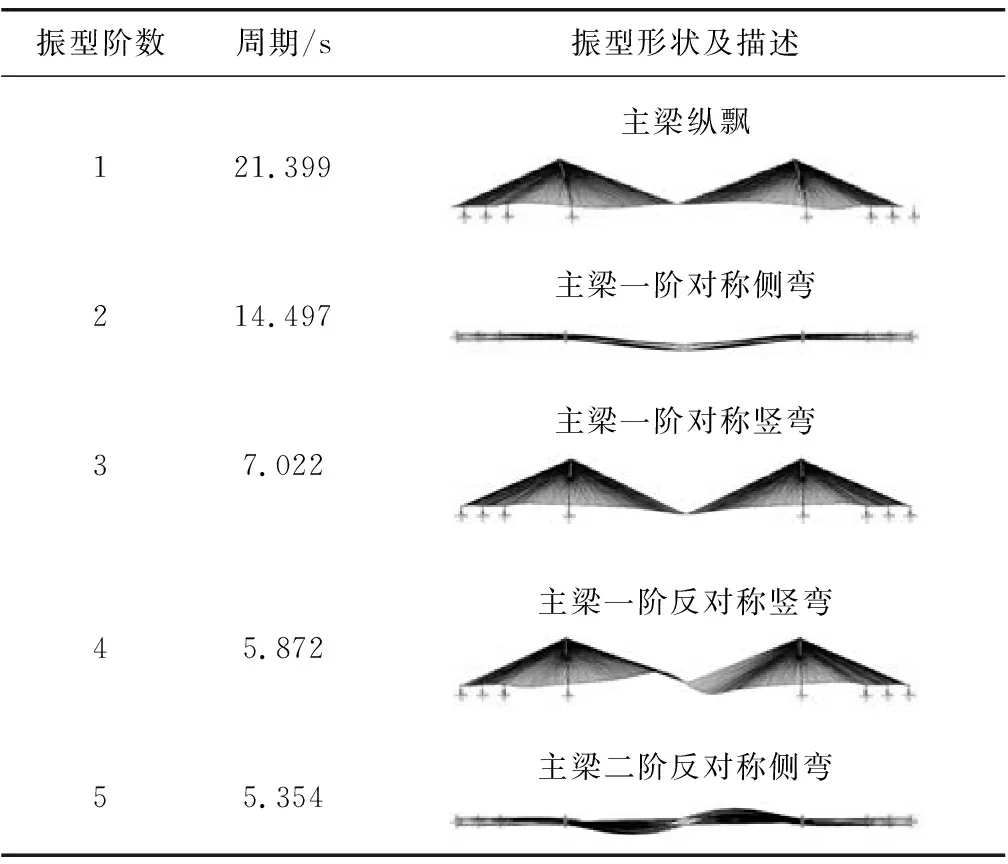
表2 主桥动力特性Table 2 Dynamic characteristics of main bridge

采用江苏省地震工程研究院提供的苏通大桥桥址处的地震动参数作为地震输入，地震加速度时程选用苏通大桥北塔塔位处超越概率100年4%的一组水平向+竖向人工地震波，如图3[6]。

图3 地震加速度时程曲线Fig. 3 Seismic acceleration time-history curve

2 主桥纵向约束装置

目前大跨度桥梁的塔、梁之间设置的约束装置主要有两类：弹性连接装置和阻尼器。弹性连接装置的作用主要是提供弹性刚度,而不是耗能。阻尼器的作用主要是提供阻尼，目前较为成熟且适用于大跨度桥梁的主要是流体黏滞阻尼器。弹性连接装置的参数是弹性连接刚度K,而阻尼器的参数主要是阻尼常数C和速度指数ξ。流体黏滞阻尼器的阻尼力与速度的关系可表达为

FD=Cvξ

(1)

式中：FD为阻尼力；C为阻尼系数；v为速度；ξ为阻尼指数(常用值一般在0.2～1.0范围内)。

对于塔、梁间纵向约束采用黏滞阻尼器的设计方案，为了研究阻尼器参数对斜拉桥结构抗震性能的影响，分别采用5个阻尼常数、4个速度指数对主桥有限元模型进行非线性时程分析。分析中采用的参数变化范围为C=5 000～40 000 kN/(m/s)；ξ=0.2～0.5，结构响应与参数变化相互关系的分析结果如图4。

图4 结构响应与参数变化相互关系Fig. 4 Relationship between structural response and parameter change

由图4(a)、(b)可以看出，随着阻尼常数C值的增加，主梁梁端位移和主塔塔顶位移先迅速减小，当C>20 000 kN·s/m后继续增大C值对位移的控制作用不大；阻尼器的速度指数ξ在0.2～0.5之间变化时对主梁梁端位移和主塔塔顶位移的影响较小。

由图4(c)可以看出，当C<10 000 kN·s/m时，北塔塔底截面的弯矩响应随着C值的增大迅速减小，随着速度指数ξ的增大而增大；当C>10 000 kN·s/m时，北塔塔底截面的弯矩响应随着C值的增大缓慢增大, 随着速度指数ξ的增大而减小。由图4(d)可以看出，在ξ=0.2和0.3时，南塔塔底截面的弯矩在C<20 000 kN·s/m时，随着C值的增大迅速减小；当C>20 000 kN·s/m时，随着C值的增大而增大。在ξ=0.4和0.5时，南塔塔底截面的弯矩在C<30 000 kN·s/m时，随着C值的增大迅速减小；当C>30 000 kN·s/m时，随着C值的增大而缓慢增大。

结合图4中关键节点位移响应和关键构件截面内力响应的计算结果可以发现，对于笔者研究的斜拉桥结构，非线性流体黏滞阻尼器的设计参数取为C=20 000 kN·s/m,ξ=0.3时减震效果较为合理。

为了研究弹性索设计参数对主桥抗震性能的影响，将弹性索的刚度K在5 000～50 000 kN/m范围取值时，主桥主梁纵飘振型的周期如表3。采用线性时程法对主桥在纵向+竖向地震输入下的地震响应进行分析，得到主桥北侧梁端位移及北塔塔顶位移响应的结果如图5，主塔塔底截面弯矩的结果如图6。

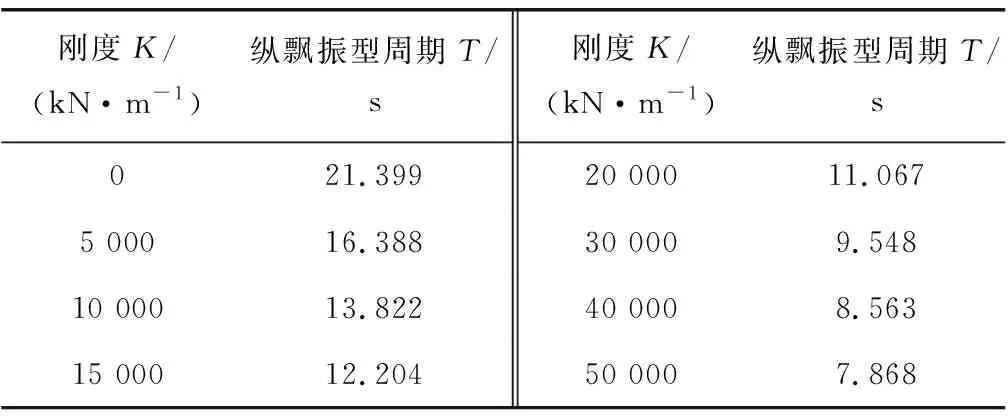
表3 弹性索刚度K与纵飘振型周期关系Table 3 Periodic relationship between the elastic cable stiffness K and the longitudinal flitting mode

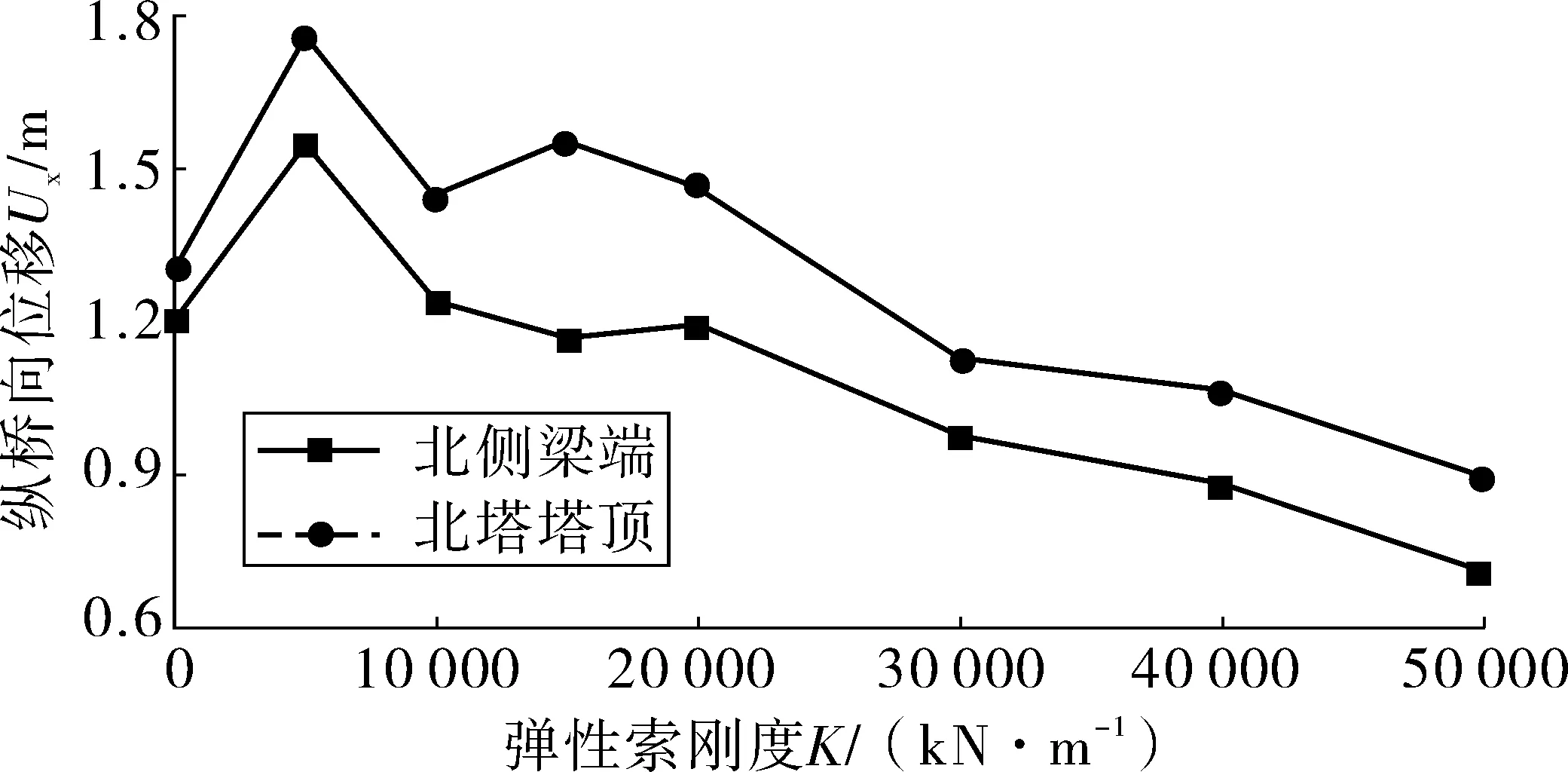
图5 关键节点位移与弹性索刚度关系Fig. 5 Relationship between the displacement of key nodes and the stiffness of elastic cable

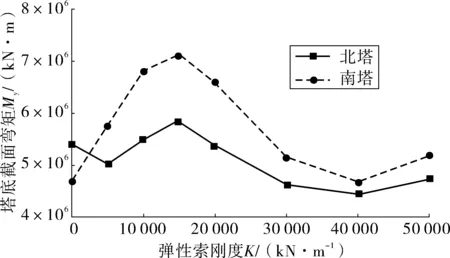
图6 塔底截面弯矩与弹性索刚度关系Fig. 6 Relationship between the bending moment of the bottom section of the tower and the stiffness of the elastic cable

由图5可以看出，当弹性索刚度K<5 000 kN/m时，增大弹性索刚度会增加主桥梁端和塔顶的纵桥向位移响应；当K>5 000 kN/m后，主桥梁端和塔顶的纵桥向位移响应随着弹性索刚度的增加总体呈逐渐减小的趋势。由图6可以看出，在弹性索刚度K由5 000 kN/m增大到15 000 kN/m时，主塔塔底截面弯矩响应随着弹性索刚度的增加而增大；当K由15 000 kN/m增大到40 000 kN/m时，主塔塔底截面弯矩响应随着弹性索刚度的增大而减小；当K>40 000 kN/m后，继续增大K值会使得主塔塔底截面弯矩响应随之增大。

结合图5和图6的计算结果可以看出，弹性索的刚度K的值取为40 000 kN/m时，采用弹性索能够有效控制主桥关键节点位移，同时对主塔塔底截面的弯矩响应的影响相对较小。

3 行波效应分析

随着斜拉桥跨径的增加，地震波在塔、墩间传播的时差也会增大，在抗震分析中行波效应问题变得越来越突出。笔者采用大质量法考虑行波效应，根据文献[7]对其进行计算。计算原理如下：

对于需要考虑非一致激励影响的结构，运动方程可由式(2)分块表示：

(2)

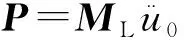
(3)

式(3)展开的第2个方程为

(4)

式(4)中ML比其他值大几个数量级，式(4)可以简化为

(5)

即输入的地震加速度与支座节点处的绝对加速度几乎相同。

笔者在分析行波效应对主桥地震响应的影响时，不考虑群桩基础的作用；修改已经建立的有限元模型，在塔、墩承台底节点除纵桥向平动位移约束释放外，其余的平动和转动自由度全部采用固定约束。在塔、墩承台底节点指定附加大质量及纵桥向节点荷载，大质量的重量取为全桥重量的一百万倍，节点荷载定义为输入的水平向地震加速度与节点上指定的大质量的乘积。参考文献[5]可知，地震动水平视波速Vapp取值从500 m/s开始选取，因为更小的的水平视波速缺乏实际意义。在下文的分析中，视波速的取值分别为500、1 000、2 000、3 000、5 000、10 000 m/s。

鉴于大跨斜拉桥抗震设计时一般会采用漂浮体系与纵向约束装置的组合体系[6]，因此为了比较不同约束方式下的主桥在考虑行波效应的非一致激励和一致激励的响应结果，笔者对以下3种情况的主桥模型分别进行了分析：

1)主梁在主塔处无纵向位移约束措施，下文简称“纵飘”。

2)主梁与主塔交点处纵向设置非线性流体黏滞阻尼器，下文简称“阻尼器”；阻尼器的设计参数为C=20 000 kN·s/m,ξ=0.3。

3)主梁在与主塔交点处纵向组合使用弹性索和阻尼器，下文简称“弹性索+阻尼器”；弹性索的刚度K=40 000 kN/m，阻尼器设计参数与2)中相同。

为了便于比较，采用大质量法分析了一致输入下主桥的最大地震响应，部分计算结果如表4。

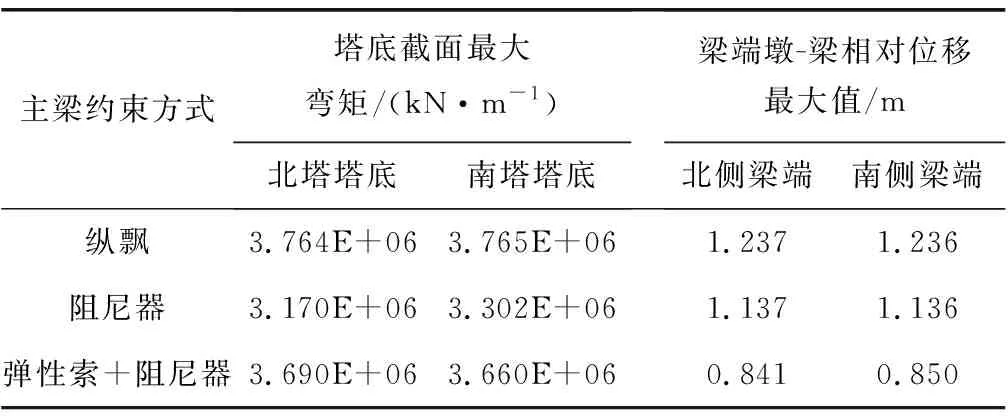
表4 一致激励时塔底截面最大弯矩及梁端墩-梁相对位移最大值Table 4 The maximum bending moment of pier bottom section and the maximum relative displacement of beam end pier and beam when uniform excitation is applied

由表4可以看出，塔、梁直接单独采用阻尼器时主塔塔底截面在地震下的弯矩响应最小，弹性索+阻尼器的方案次之，无减震措施的主梁纵飘方案最大。地震下主桥边墩-主梁之间的纵桥向相对位移最大的方案为无减震措施的主梁纵飘方案[7]，阻尼器方案次之，弹性索+阻尼器的方案最小。

对于主桥的某一响应量，设其在一致激励下的最大值为RUE，考虑行波效应时的最大响应值为RTW，定义变量λ=RTW/RUE作为考虑行波效应的影响系数。对于以上3种不同的主梁约束方式，在不同视波速下主桥各响应量的结果如图7。由图7(a)、(b)可以看出，对于3种不同主梁纵桥向约束方式的主桥，考虑行波效应时，主塔塔底截面的弯矩响应计算结果与一致激励时的对应值相比，可能增大的幅度在20%左右。对于主梁梁端处墩-梁最大相对位移，由图7(c)、(d)可以看出，主桥在塔-梁之间单独采用阻尼器进行纵桥向减震时考虑行波效应的计算结果小于一致激励时的对应值；主梁纵桥向采用漂浮体系或塔-梁间采用弹性索+阻尼器的纵桥向减震方案，地震波传播的视波速Vapp<2 000 m/s时，考虑行波效应的计算结果与一致激励的对应值相比可能增大的幅度小于10%；当Vapp>2 000 m/s时，考虑行波效应的计算结果略小于一致激励的对应值[8]。

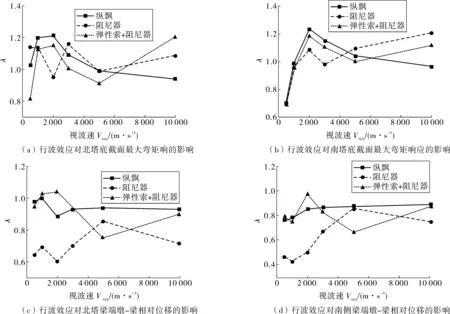
图7 行波效应对主桥各响应量的影响Fig. 7 Influence of traveling wave effect on the response of the main bridge

4 结 论

以一座主跨1 500 m的斜拉桥设计方案为研究对象，对减震措施及行波效应对主桥地震响应的影响进行了分析，得到了如下结论：

1)主桥塔、梁之间采用阻尼器进行连接的减震方案对减小一致地震激励下主塔塔底截面内力响应的效果最好；主桥塔、梁之间采用阻尼器和弹性索组合的方案对减小一致地震激励下主梁-边墩之间最大相对位移的效果最好。

2)考虑行波效应的计算结果与一致输入的计算结果相比，主塔塔底截面内力响应在3种不同的主梁纵桥向约束方式下均有可能增大约20%左右。

3)对于主梁纵飘设计方案及主梁纵桥向采用阻尼器与弹性索组合的减震设计方案，边墩-主梁之间的最大相对位移考虑行波效应时与不考虑的情况相比可能增大的幅度不超过10%；对于主梁纵桥向仅采用阻尼器减震的设计方案，边墩-主梁之间的最大相对位移考虑行波效应时与不考虑的情况相比会有所减小。

总之，对于千米级斜拉桥的抗震设计，采用漂浮体系时无论是否采用纵桥向约束装置，若不考虑行波效应问题都有可能导致偏于不安全的设计结果。