基于马鞍地形的无线传感器网络节点定位算法*

胡中栋,张 康,王振东

(江西理工大学信息工程学院,江西 赣州 341000)

无线传感器网络WSN(Wireless Sensor Network)的出现引起了全世界范围的广泛关注。1999年,著名的美国商业周刊将无线传感器网络列为21世纪最具影响的21项技术之一[1-2];2003年,MIT技术评论(Technology Review)在预测未来技术发展的报告中,将其列为改变世界的10大新技术之一[3]。环境监测与预报、森林防火、地质灾害监测与预警等是无线传感器网络的重要应用领域。节点定位是无线传感器网络应用的重要基础,是当今无线传感器网络研究热点之一[4]。在无线传感器网络的应用中,位置信息对传感器网络的监测活动至关重要。如在大面积环境监测中需要知道污染源发生的地点;森林火灾灾情监测中,需要知道火灾发生的地域[5-7];在地质灾害监测预警中,必需要知道发生险情的时间与地域,以便迅速采取有效行动。

现有的大多数无线传感器网络定位技术都是假设应用在理想环境下提出的。例如三维的定位算法适合三维自由空间内的节点随机分布情况,即假定信号传输模型为理想的球体。而无线传感器网络实际应用环境往往是山区。如果用三维自由空间的定位算法来确定山区地形上的节点位置,往往无法达到节点定位的精度要求。因此,研究适合山区地形无线传感器网络节点定位算法具有重要意义。例如张亚杰、段渭军等提出了改进的距离重构三维定位算法[8];廖兴宇,余 敏,汪伦杰提出了基于锚球交域投影质心的WSNs三维定位算法[9];屈军锁,侯晓宁等提出了四基站时差和牛顿迭代法的三维定位算法[10]等都是三维自由空间的定位算法。胡中栋、谢金伟、肖华为研究了基于山头地形和基于山区地形的无线传感器网络节点的定位算法[11-13]。本文提出了基于山区马鞍地形无线传感器网络节点定位算法(NLA-ST)。

1 无线传感器网络定位技术

无线传感器网络定位技术分为基于测距定位方法和非测距定位方法[14]。基于测距定位方法定位精度高,但需要增加硬件成本。非测距定位方法受环境因素的影响小,虽然定位精度更低,但能够满足多数无线传感器网络应用的要求,因此备受关注。非测距定位方法主要有质心算法、DV-Hop算法、Amorphous 算法、APIT算法等,其中影响最大、应用最广泛的当属DV-Hop算法[15]。

1.1 三维DV-Hop定位算法

Niculescu D等人提出了DV-Hop算法,距离矢量路由原理是此算法的主要原理。算法通过广播在所有节点间进行信息交换,得到每一个节点到其他节点的最小跳数。所有的未知节点根据到锚节点的最小跳数乘以每跳平均距离估算出到该锚节点的距离。根据以上信息通过最小二乘法(极大似然估计法)计算自身坐标[16]。若未知节点的坐标为(x,y,z),已知该未知节点到所有锚节点的距离为d1,d2,…,dn(n≥4),对应的锚节点坐标为(x1,y1,z1),(x2,y2,z2),…,(xn,yn,zn)。

可得矛盾方程组:

AX=B

(1)

若矛盾方程组有解则可得:

X=(ATA)-1ATB

(2)

1.2 性能评价

一般用相对定位误差来评价算法的性能。

若某个未知节点的估算坐标(xi,yi,zi)和实际坐标(ai,bi,ci)差距Δdi为:

(3)

则n个未知节点的平均定位误差Δ可表示为:

(4)

2 基于马鞍地形的节点定位算法

山区地形是由山头地形、山谷地形、山脊地形和马鞍地形等组成的复杂地形。在山区地形上应用无线传感器网络的传统非测距定位算法,其定位精度较低。所以需要研究适合山区地形上的节点定位算法,以提高传感器节点定位精度。本文研究基于马鞍地形的节点定位算法NLA-ST(Node Location Algorithm Based on Saddle Topography)。方法步骤如下:

第1步 建立山区马鞍地形方程。因为双曲抛物面能很好的表示山区马鞍地形,所以采用双曲抛物面作为马鞍地形的拟合函数。

双曲抛物面方程为:

x2/a2-y2/b2=z

(5)

式中:a、b为正常数。采用最小二乘的曲面拟合算法,在山区电子地形图上取一组离散点的坐标代入双曲抛物面方程(5)中,建立矛盾方程组来求拟合参数a和b,从而求得马鞍地形方程。

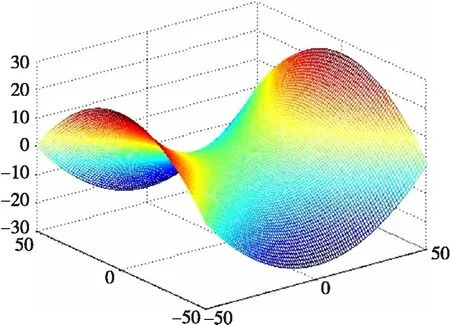
图1 山区马鞍地形

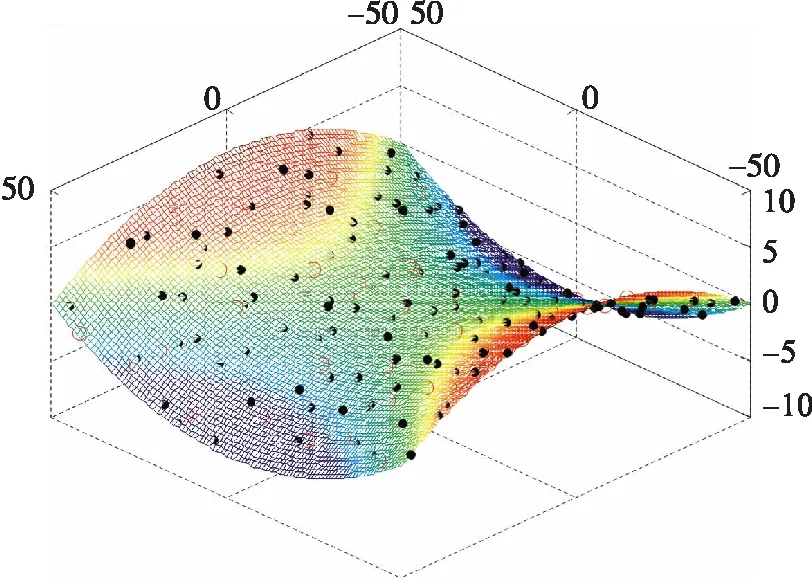
图2 传感器节点在山区马鞍地形随机分布示意图

第2步 在山区马鞍地形上应用经典三维 DV-Hop 定位算法求出无线传感器网络节点的初始位置。

第3步 将所求节点的初始位置垂直投影到马鞍地形表面上。设所求节点初始位置P(x,y,z),在马鞍地形表面上的投影点为P0(m,n,k)。通过P0(m,n,k)的法线方程可得2个关于m,n,k的方程,另外,P0(m,n,k)满足马鞍地形方程,得第3个方程。联立这3个方程,可求出m,n,k。

对双曲抛物面方程x2/a2-y2/b2=z进行等价变换:两边同等乘于a2b2得:b2x2-a2y2=a2b2z。

(1)求双曲抛物面法线方程

设双曲抛物面上任意一点。

F(x,y,z)=b2x2-a2y2-a2b2z=0

∂F/∂x=2b2x, ∂F/∂y=-2a2y, ∂F/∂z=-a2b2

法向量为:

(2b2x,-2a2y,-a2b2)

过P0(m,n,k)的法向量方程为:

(6)

由式(6)有:

整理得:

b2ym-(a2+b2)mn+a2xn=0

(7)

由式(6)还可得:

整理得:

(2z-a2)m-2mk+a2x=0

(8)

投影点P0(m,n,k)坐标满足双曲抛物面方程

b2m2-a2n2-a2b2k=0

(9)

联立式(7)～式(9)式得方程组。

由式(9)得:

k=m2/a2-n2/b2

(10)

将式(10)代入式(8)式得:

(a2-2z)m+2m(m2/a2-n2/b2)-a2x=0

整理得:

a2b2(a2-2z)m+2b2m3-2a2mn2-a4b2x=0

(11)

由式(7)得:

将上式n代入(11),并整理得:

(12)

式(12)两边同乘以[(a2+b2)m-a2x]2,并整理得:

2(a2+b2)2m5-4a2(a2+b2)xm4+a2[(a2-2z)(a2+b2)2+
2a2x2-2b2y2]m3-a4(a2+b2)(3a2+b2-4z)xm2+
a6(3a2+2b2-2z)x2m-a8x3=0

(13)

式(13)是关于m的一元五次方程。节点初始位置P(x,y,z)在马鞍地形表面上的投影点有可能有多个。如图3中P(x,y,z)有2个投影点P0(m,n,k)与P1(m1,n1,k1)。这时,就取距离节点初始位置P(x,y,z)更近的投影点作为未知节点的修正坐标。图3中投影点P0(m,n,k)距离P(x,y,z)更近,所以P0(m,n,k)即为未知节点的较正位置。

图3 所求节点的初始位置垂直投影到马鞍地形表面

(2)应用数值解方法解关于m的一元五次方程

(a)根的搜索

将式(13)转换为标准方程(m5的系数为1):

m5+a2m4+b2m3+c2m2+d2m+e2=0

(14)

若有方程:

f(x)=xn+a1xn-1+a2xn-2+…+an-1x+an=0

则该方程根的绝对值(即根模)的上下界有如下结论:

若a=max{ |a1|,|a2|,…,|an| },则方程的根的绝对值小于a+1

对式(14)有:

aa=max{|a2|,|b2|,|c2|,|d2|,|e2| }

式(14)的根的绝对值小于(aa+1),则根的搜索区间为:

分析表3和图4可以得出，应用了RANSAC算法后，拟合结果与理论值更加接近，且稳定性亦有所提高，验证了本文方法的准确性。从表4及图5中可以看出，运用本文方法与传统方法拟合耗时相当，但本文方法的鲁棒性较强且拟合精度更高。

[-(aa+1),(aa+1)]

设无线传感器网络节点分布范围是[a,b]。由于我们只需要求出范围[a,b]内的根。因此,如果[-(aa+1),(aa+1)]范围超出[a,b],则从节点的分布范围[a,b]搜索方程的有根区间。

(b)用二分法求方程(14)的数值解

方程:f(x)=0,在区间[a,b]内有唯一一个根。

①准备:计算f(a),f(b);

②二分:计算f((a+b)/2);

③判断:如果f((a+b)/2)=0,则(a+b)/2为f(x)=0 的根,否则检验:

若f((a+b)/2)·f(a)<0,则方程的根位于[a,(a+b)/2]内,以(a+b)/2代替b;

若f((a+b)/2)·f(b)<0,则方程的根位于[(a+b)/2,b]内,以(a+b)/2代替a;

④若|b-a|<ε(ε为精度要求),计算终止,此时x*=(a+b)/2;否则转②。

如果方程只有唯一的实数根,该数值解就是所求的初始位置P(x,y,z)在马鞍地形上的投影,也就是所求未知节点的二次估测坐标。如果方程有n个实数根,找出n个根中距离所求出的未知节点初始位置P(x,y,z)最近的那个根,即为未知节点的修正坐标。显然,该节点的定位精度更高。如果方程无实数根,则所求的初始位置P(x,y,z)就是未知节点的最终坐标。

通过实验发现有时可能会有极个别节点对应的一元五次方程无实数解,这时就用DV-HOP算法求出的初始位置作为节点的最终坐标。

3 仿真实验

为了检验算法的性能,在理想的马鞍地形环境中,对经典三维DV-Hop定位算法、改进的三维DV-Hop定位算法和NLA-ST马鞍地形定位算法在MATLAB平台上进行了仿真对比分析。研究了不同马鞍地形与定位误差的关系、不同锚节点比例与定位误差的关系以及不同通信半径R与定位误差的关系。每次仿真都是在马鞍地形中均匀随机布放200个节点,马鞍地形在水平面的投影范围是100 m×100 m。图2是一次仿真实验的无线传感器网络节点均匀随机分布图。

3.1 不同马鞍地形的仿真实验

仿真实验环境:通信半径R=40 m,节点总数为200个,锚节点50个,占25%。用双曲抛物面方程模拟马鞍地形。改变式(5)中的参数a和b(设a=b),分别对a=5、10、15、20、25、30、35和40进行仿真实验。对每个不同参数a都分别进行了50次实验,然后取相对均方误差的平均值。每次实验中未知节点和锚节点的坐标都是随机产生的,实验结果如图4所示。由图4可知,NLA-ST马鞍地形定位算法精度明显高于传统定位算法。NLA-ST定位算法精度比经典三维DV-HOP定位算法平均提高221.5%,比改进的三维DV-HOP定位算法平均提高218.5%。经典三维DV-HOP定位算法与改进的三维DV-HOP定位算法受马鞍地形参数的影响很大,且误差也很大,平均相对定位误差分别为116.2%和115.3%,难于满足实际定位需要。NLA-ST定位算法精度高,平均相对定位误差36.6%,能满足实际应用的需求。

图4 不同马鞍地形的平均相对误差曲线

3.2 不同锚节点比例的仿真实验

仿真实验环境:通信半径R=30 m,马鞍地形的参数a=b=20,分别对锚节点占15%,25%,35%,45%和50%时进行了仿真实验。对不同锚节点比例的仿真都进行了50次,然后取相对均方误差的平均值。每次实验中未知节点和锚节点的坐标都是随机产生的,实验结果如图5所示。由图5可知,马鞍地形节点定位算法精度明显高于传统定位算法的精度。锚节点比例越大,定位精度越高。NLA-ST定位算法精度比经典三维DV-HOP定位算法平均提高156.6%,比改进的三维DV-HOP定位算法平均提高151.6%。经典三维DV-HOP定位算法与改进的三维DV-HOP定位算法在马鞍地形上定位误差均较大,平均相对定位误差分别为85.7%和84.2%,难于满足实际定位需要。NLA-ST定位算法精度高,平均相对定位误差33.2%,能满足实际应用的需求。

图5 不同锚节点比例的平均相对误差曲线

3.3 不同通信半径的仿真实验

仿真实验环境:无线传感器节点总数200,锚节点50,锚节点比例25%,马鞍地形的参数a=b=20,分别对通信半径R=30 m,35 m,40 m,45 m,50 m,55 m,60 m时进行了仿真实验。对每种通信半径仿真都进行50次,然后取相对均方误差的平均值。每次实验中未知节点和锚节点的坐标都是随机产生的,实验结果如图6所示。由图6可知,3种方法的定位精度与通信半径关系不大。NLA-ST定位算法精度明显高于传统定位算法的精度。马鞍地形节点定位算法精度比经典三维DV-HOP定位算法平均提高154.6%,比改进的三维DV-HOP定位算法平均提高148.1%。经典三维DV-HOP定位算法与改进的三维DV-HOP定位算法在马鞍地形上定位误差均较大,平均相对定位误差分别为82.0%和79.9%,难于满足实际定位需要。NLA-ST定位算法精度高,平均相对定位误差32.2%,能满足实际应用的需求。

图6 不同通信半径的平均相对误差曲线

4 结束语

经典三维DV-HOP定位算法与改进的三维 DV-HOP 定位算法在马鞍地形上定位误差均较大,而且受马鞍地形的变化影响较大,无法满足实际应用需求。本文研究山区马鞍地形上无线传感器网络的非测距定位算法。NLA-ST马鞍地形定位算法利用了马鞍地形的特点,大大提高了节点定位算法的精度。不论马鞍地形如何变化,该定位算法的误差均比较小,完全能满足实际应用的需要。