光纤法珀腔声传感器理论与仿真分析研究*

程 进,邹小平

(北京信息科技大学传感技术研究中心,北京市传感器重点实验室,教育部现代测控技术重点实验室,北京 100101)

作为一种新型声传感器,光纤声传感器与现有电动式、压电式、电容式等传统的声-电直接转换原理的声传感器相比,具有灵敏度高、抗电磁干扰、传输损耗低、耐腐蚀、体积小、重量轻等优点,在环境噪声监测、噪声源定位、光声探测[1]等应用领域也有广泛的需求,特别是对强电磁干扰环境下的声波拾取具有不可替代性[2]。因此光纤声传感器得到广泛研究。

光纤声传感器根据调制光学参量的不同,可分为强度型、相位型、波长型、偏振型等,其中研究较多的主要强度型和相位型光纤声传感器。强度型光纤声传感器的研究开展的较早,它原理简单,易于实现,目前已商品化。相对于相位型光纤声传感器,它的灵敏度较低、本底噪声较大[3],不能满足于微弱声信号的应用,如微弱语音拾取、远距离声源定位、光声探测等。相位型光纤声传感器是基于超高灵敏的光干涉技术,具有灵敏度高、本底噪声低等优点,因此目前是声传感器的前沿研究热点之一[4]。

相位型光纤声传感器是通过不同的干涉结构实现的[5],包括迈克尔逊、马赫-曾德尔、法珀腔、萨格纳克环等干涉结构。在这些干涉结构中,法珀干涉结构只需一根光纤,该光纤的端面与敏感体的反光面形成法珀腔,该结构简单,特别适合制作声传感器。目前关于光纤法珀腔声传感器的研究主要涉及如下几个方向:①法珀腔的设计[6-14],包括采用不同结构、不同的振膜、不同材料制作光纤法珀腔声传感探头;②信号解调方法研究[15-16];③稳定性研究[17-18]等。目前光纤法珀腔声传感器还没有实用化,在实用化过程中,需要对其进行较为系统的理论与仿真分析研究,然而目前关于这方面的研究鲜有报道。

本文根据光纤法珀腔声传感器的原理结构,对其敏感机理进行了理论分析,采用ANSYS软件对振膜的预应力振动模态和预应力谐响应进行了有限元仿真,并对其关键参数灵敏度、动态范围进行了分析。本文对光纤法珀腔声传感器的实应化研究具有指导作用。

1 光纤法珀腔声传感器原理结构

光纤法珀腔声传感器的原理结构如图1所示,它的核心结构包括敏感声波的振膜和光纤,其中振膜的反光面和光纤端面组成光纤法珀腔。

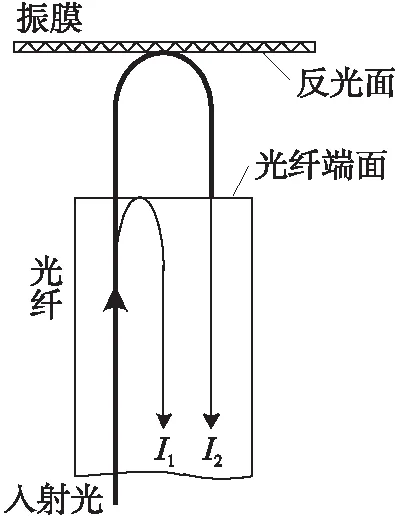
图1 光纤法珀腔声传感器的原理结构图

在该结构中,从光纤导入的入射光,在光纤端面会发生反射,形成反射光I1,从光纤端面透射的光经振膜反光面反射,并耦合入光纤,形成反射光I2。由于光纤端面的反射率很低(约为4%),振膜反射的光经光纤端面反射后强度非常弱,可以忽略。因此,该结构为一低精度法珀腔,其输出的光信号等效于双光束干涉信号。

该结构敏感声波的原理是:声波作用于振膜后,引起振膜做受迫振动,该振动会引起光纤法珀腔长度发生变化,使I1和I2的相位差发变化,从而调制输出的干涉信号;通过对干涉信号的解调,得到相位变化,即得到声波信号。

2 光纤法珀腔声传感器的敏感机理

光纤法珀腔声传感器拾取的是动态声波信号,对于这种信号,采用单色光源,利用强度解调是一种简单有效、成本低的方法。下面,将从数学上给出,光纤法珀腔声传感器工作在单色光情况下,实现声波信号解调的敏感机理[19]。

低精细度光纤法珀腔的干涉可近似为双光束干涉,其干涉光强可写为:

I=I0[1+γcos(Δφ+φ0)]

(1)

式中:I0=(Imax+Imin)/2,Imax为干涉光谱光强极大值,Imin为干涉光谱光强极小值,γ=(Imax-Imin)/(Imax+Imin)干涉对比度,φ0为初始相位,对于法珀腔,φ0=4πnL/λ,λ为工作光波长,Δφ为外界变化引起的干涉光的相位变化。对于声波信号,Δφ可写为:Δφ=φssin(ωt),φs为声波信号引起的相位振幅。

在此声波信号作用下,光纤法珀腔的输出信号为:

I=I0{1+γcos[φssin(ωt)+φ0]}

(2)

对上式进行频谱分析,可得:

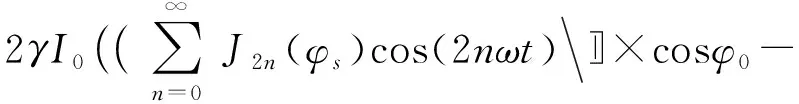
(3)

声波是一交流信号,上式中第一项是直流分量,因此取上式的交流分量,该光信号经过光电探测器后得到的光电流信号为:

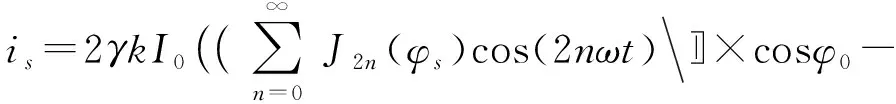
(4)

式中:k为光电转换系数。要保证获得稳定的信号,通过上式可知,必须保证两光束的初始相位恒定不变,即保证φ0不变。

此外,由式(4)可以看出,相应于声波频率ω的成分的信号幅度正比于sinφ0,为了使这个信号的幅度最大,即传感器的灵敏度最高,φ0应当尽可能接近于π/2,即光纤法珀腔应工作在正交工作点处。

当光纤法珀腔声传感器工作在正交工作点时,即φ0=π/2,式(4)中信号频率成分为ω的偶次倍频的分量均为0,此时,光电流信号可以简化为:

(5)

考虑小信号声波,当φs很小时,式(5)表示的信号中,频率为ω的基波分量将成为主要成分,且J1(φs)≈φs/2,此时,可得:

is=γkI0φssin(ωt)

(6)

式(6)即为光纤法珀腔声传感器的敏感机理。

不过需要注意的是,按式(6)工作的光纤法珀腔声传感器需要满足3个条件:①采用单色光作为工作光;②初始相位为π/2的奇数倍,即正交相位点;③声波引起的振膜振动导致的相位变化幅度不能太大。

上述敏感机理还可以通过物理图像进行表达,如图2所示。从图2中可以看出,声波信号的解调是利用干涉光谱的一个线性区间光强的变化实现的,即声波引起振膜振动,该振动引起腔长变化,相应于相位作周期性变化,在一个线性区间上,该变化对应于光强变化,经光电转换后,输出声波信号。在正交工作点时,光强的变化率最大,即灵敏度最高,同时为了保证输出的声波信号不失真,声波引起的相位变化最大不能超过干涉光谱的一个线性区间。

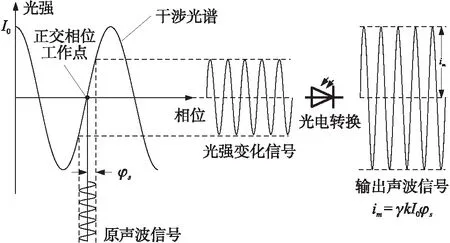
图2 光纤法珀腔声传感器敏感机理图

3 光纤法珀腔声传感器有限元仿真分析

3.1 有预应力的振动模态

光纤法珀腔声传感器敏感声波的部件是振膜,声波引起振膜的振动,通过光纤法珀腔结构拾取振膜的振动信号,从而实现对声波的敏感。

振膜的振动情况对光纤法珀腔声传感器的灵敏度、频率响应、动态范围等关键指标参数有重要影响,因此需要对振膜的振动进行仿真分析,以获取振动模态、谐响应等动力学特性,这对于光纤法珀腔声传感器设计十分重要。下面利用ANSYS软件进行有限元仿真分析。

①预处理

光纤法珀腔声传感器的振膜是安装于有支撑结构的外壳上,它将使振膜处于绷紧的状态,即膜内有张应力。振膜后方为一体积较大的腔体,腔内气体对振膜振动的阻尼作用可以忽略不计,因此该振膜的振动可简化为简支圆形薄膜振动,它可以抽象为一有张应力的简支薄膜,在进行有限元分析时,必须要考虑张应力的作用,才能得到振动模态的频率值。下面利用ANSYS进行有预应力的模态分析。

②前处理

取振膜直径为20 mm,振膜的厚度为10 μm,振膜材料为金属镍,密度为8 800 kg/m3,杨氏模量为2.1×1011Pa。由于膜厚相对膜的直径极小,因此取泊松比为0。单元选取Membrane Shell Elements(SHELL41),它是一个3D单元,有实常数,即为膜的厚度。因此在建模时,只需要根据振膜的大小生成一个平面圆,振膜的厚度通过实常数进行加载。

为了获得张应力,ANSYS提供通过温度变化的方式实现。因此还需要设置材料的热膨胀系数,13×10-6m/(m· ℃),并设参考温度为0 ℃。

③求解

ANSYS在进行有预应力的模态分析时,需要分为两个求解步骤。

第一步:进行静力分析。

计算结构内的预应力,特别需要注意的是这一步需要键入打开预应力命令“pstres,on”。预应力是通过温度变化产生的,根据公式:

η=EαtΔT

(7)

和设定的应力值,计算温度变化。式中E为杨氏模量,α为热膨胀系数,t为膜的厚度,ΔT为温度变化,η为厚度为t的薄膜单位长度所受的力,η的单位为N/m。

镍薄膜单位横截面上能承受的最大应力为P=4×108N/m2,因而对于膜厚为10 μm的镍膜,η=4 000 N/m。根据此值和材料的其参数,可得温度变化应设为-146.52 ℃。

对模型的所有点进行位移约束,设置位移值为0,通过降温,使膜内产生均匀应力。分析类型为静态(static),进行求解。求解完毕,需要确认应力计算结果是否正确。

通过观察应力计算结果,可以看出,在膜的界出现了一对作用力与反作用力,如图3(a)所示,正是这一对作用力,使膜内产生应力。进一步对过后处理观察应力计算结果,如图3(b)所示,膜内的应力分布均匀,且应力大小为4×108N/m2,这与设定值是一致的。

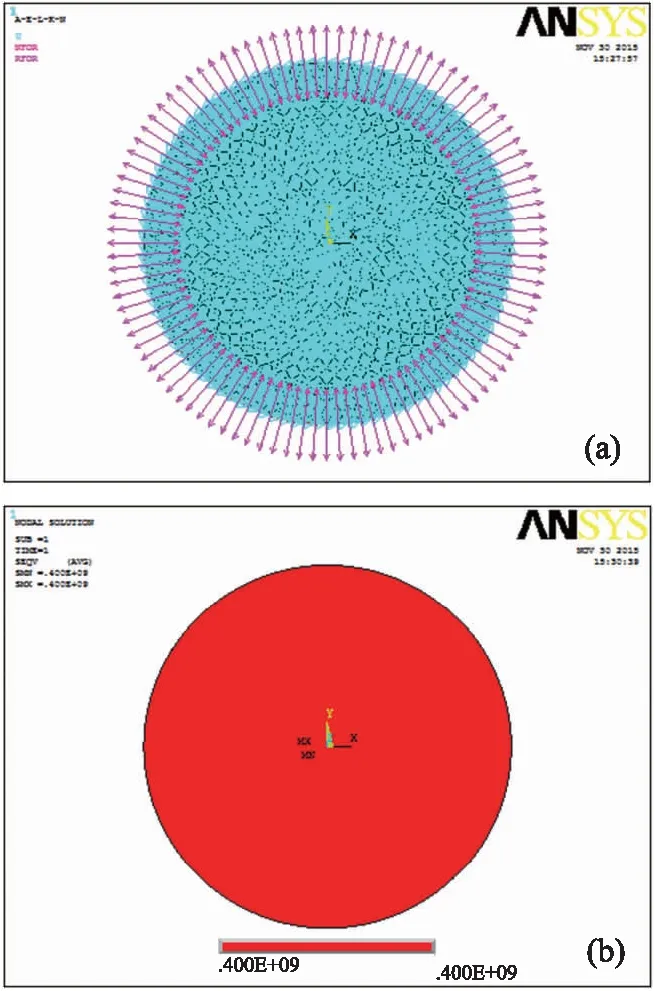
图3 静力求解结果(a)和膜内应力分布(b)

第二步:进行预应力模态分析。

在完成静力分析后,需要去掉静力分析时的边界条件,然后选择分析类型为模态(modal),并打开预应力命令“pstres,on”。在该类型分析中,需要设置计算的模态数量,本次分析设置为20,分析的频率范围采用默认值,并注意设置将每个子步的计算结果写入文件中,以保证后处理时可以正确查看每个模态的结果。

设置模态分析时的边界约束条件:对振膜周边的节点的所有自由度进行约束,设位移值为0,对于振膜内部除边界的所有节点,设置x,y方向位移为0,即振膜在外界作用下,只能沿横向振动。设置完成后求解,并查看结果。

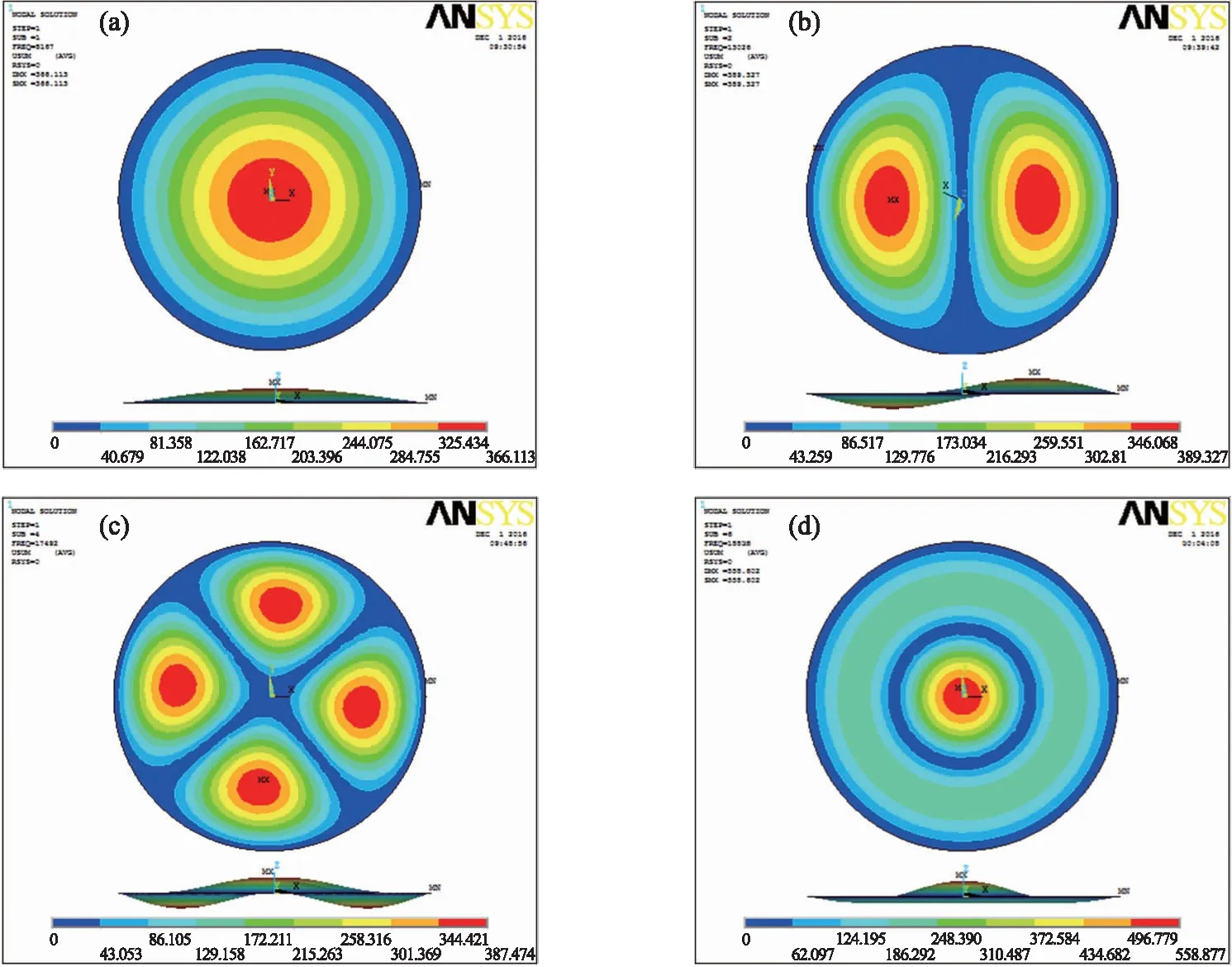
图4 模态数为1(a),2(b),4(c),6(d)时的振动模态图

表1给出了前6个模态的振动频率,其中1阶模态的频率是振膜振动的固有频率,其值为8 162.6 Hz。根据仿真分析所用的参数,利用集中参数计算振膜固有频率的公式:

式中:振膜半径a=10 mm,密度ρ=8 800 kg/m3,单位横截面上承受的应力为P=4×108N/m2,可计算出f=8 146 Hz。在施加同样大小的预应力情况下,仿真计算的值与理论值的偏差为0.20%,这表明仿真结果是真实可靠的。

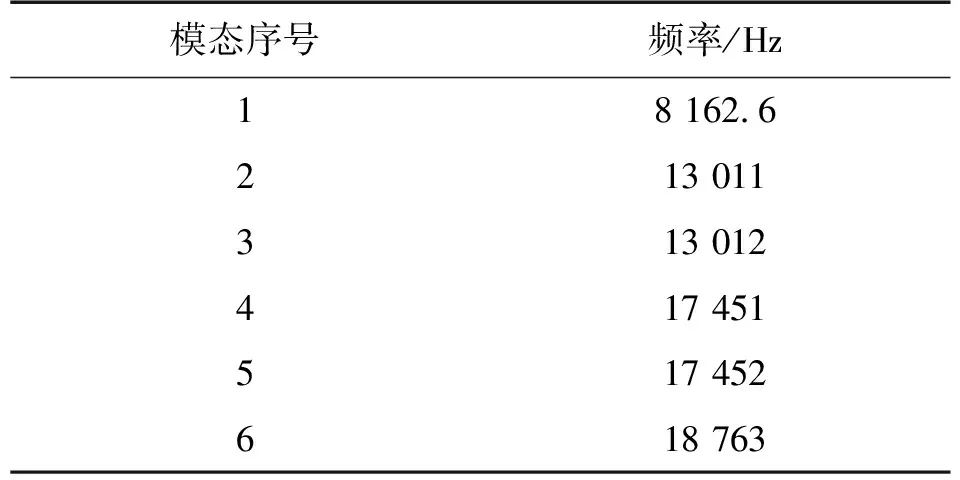
表1 预应力模态求解结果

通过有限元不仅能够得到各个模态的振动频率,还可以直观的得到各个振动模态的振形,通过观察不同振动模态的振形,可以更好的理解声传感器的工作过程,并通过参数设计,使声传感器工作在期望的模态下。

如图4所示,为求解的频率为8 162.6 Hz,13 011 Hz,17 451 Hz,18 763 Hz对应的振动模态振形图。从图中可以看出,一阶振形是振膜整体起伏,振膜中心处振幅最大。而所有的高阶模态,振膜内都存在不同相位振动区域,出现这种情况时,传感器将不会工作在线性区,并出现严重的谐波失真。

3.2 有预应力的谐响应ANSYS分析

谐响应分析可以获得振膜在外界作用下频率响应特性。进行有预应力的谐响应分析,首先要进行预应力分析,之后选择谐响应(harmonic)分析类型。分析采用的有限元单元类型、材料参数、预应力的施加方式都与前文相同。

在完成预应力分析后,进入谐响应分析设置,设置分析方法为完全法,分析的频率范围100 Hz～40 kHz,分为400个子步,边界约束条件与模态分析一致。外加1 Pa的压力载荷。并设置每个子步的计算结果都输出存储(以保证有可调用的数据结果)。然后计算。

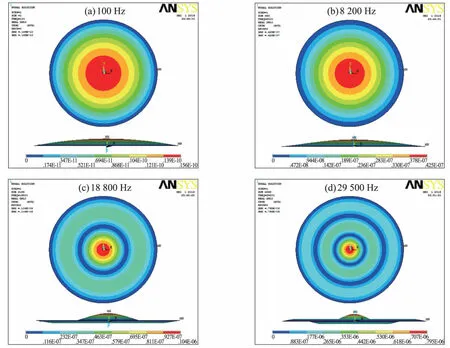
图6 在100 Hz(a),8 200 Hz(b),18 800 Hz(c)和29 500 Hz(d)激励下振膜的振动模态

通过时间频率后处理器(/post26)读取结果。通过提取振膜中心附近的节点的Z方向振幅,可以得到在分析的频率范围内,频率响应特性。如图5所示为在100 Hz～40 kHz范围内振膜的频率响应特性,从图中可以看出,一阶共振频率为8 200 Hz,再往高频段区间还有两个共振峰,这些频率与之前的模态分析的频率很好的吻合(注:误差是由于计算的步长引起的。)

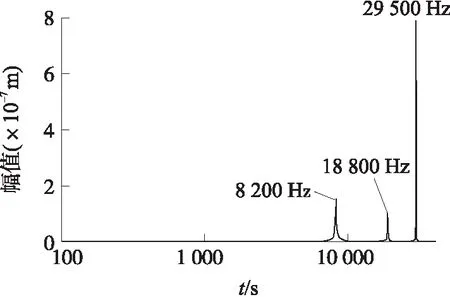
图5 在100 Hz～40 kHz范围内振膜的频率响应特性

至于频率响应曲线上哪个段频率范围可以作为设计传感器的依据,这需要知道在各个频率段内,振膜在不同频率激励下的振动模态。为此,进一步通过后处理模块(/post1)得到了100 Hz,8 200 Hz,18 800 Hz,以及29 500 Hz等关键频率点处的振动模态图,如图6所示。

从图6可以看出,在外界作用频率低于一阶共振频率时,振膜的振形与一阶振动模态的振形一致,即低于一阶共振频率的低频率段,振膜是整体起伏的,而在高频段的两个共振频率处,出现明显的不同相振动区域。

因此,从仿真结果可以知道,对于这种基于振膜敏感声波的光纤法珀腔声传感器,只有在离开一阶共振频率的低频段才具有良好的频率响应特性。

4 光纤法珀腔声传感器灵敏度分析

由以上有限元仿真分析可知,光纤法珀腔声传感器的振膜在工作时是整体起伏的,如图7所示,设振动的振幅为dm,振膜的半径为a、面度为σ、膜内张力为T、膜的振动基频为f0、声压为P,则f0与其他参数的关系为[20]:

(8)

图7 光纤法珀腔声传感器工作时振膜的振动示意图

在低频声波信号作用下,膜中心的振幅为:

dm=Pa2/(4T)

(9)

由振膜引起的干涉光相位变化的幅值为:

φs=4πndm/λ

(10)

式中:n空气折射率(n≈1),λ为工作光波长。

设电路的电流电压转换电阻为R,则在正弦声信号作用下,由式(6)可得传声器的灵敏度S为:

(11)

由式(8)～(11)可得:

(12)

从式(12)可以看出,光纤法珀腔声传感器的灵敏度与干涉光的强度和干涉对比度、光波长、振膜的面密度、振膜的共振频率、以及转换电阻相关。为了得到高灵敏度,需要高的干涉对比度、强度大的光强、大的转换电阻、短的光波长、小的振膜面密度、以及低的频率。其中光波长与传声器的动态范围相关,波长越长动态范围上限越大;转换电阻与传声器的本底噪声相关,阻值越小,本底噪声越底;共振频率与传声器的频率范围有关,共振频率越高,频率响应范围越大。

在实际的光纤法珀腔声传感器中,一些参数是由元器件的性能决定的,如光电转换系数k,光源的波长λ,电流电压转换电阻R,此外干涉光谱的对比度通过调节一般都能够达到0.9以上,因此,在设计光纤法珀腔声传感器时,主要关注的是光源的光功率、振膜的材料以及振膜的共振频率。

5 光纤法珀腔声传感器动态范围分析

由图8可知,光纤法珀腔声传感器的需要工作在正交相位点,且最大线性工作区间为(mπ,(km+1)π),m为整数,因此相位变化的最大幅度为π/2。根据式(10),可得相应的振膜允许最大振幅dm=λ/8n。对于1 550 nm的工作光,最大允许振幅dm≈193 nm。

对于半径a为4.5 mm、厚度为3 μm的金属振膜,在共振频率为8 000 Hz的情况下,受1 Pa(94 dB)声压作用,由式(8)、式(9)可得振膜中心的振幅为21.7 nm,由此可知,对应最允许振幅的声压为8.9 Pa,对应的有效声压为110 dB,此声压为动态范围的上限。动态范围的下限为传声器的本底噪声,需要通过实验测得。

6 实验验证

在以上理论的指导下,制作了光纤法珀腔声传感器样品,如图8所示。

图8 光纤法珀腔声传感器样品

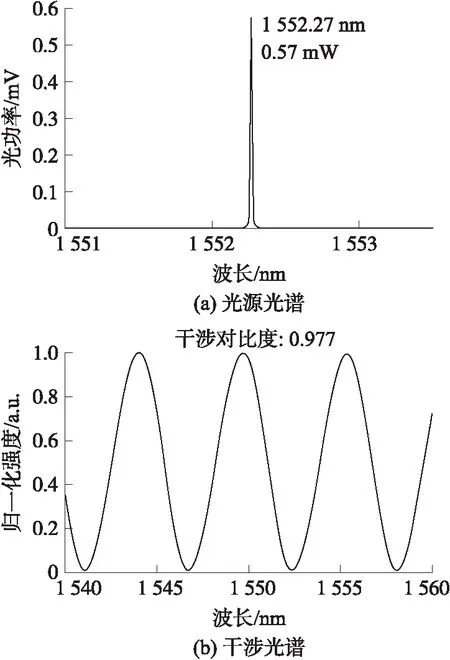
图9 光纤法珀腔声传感器的光源光谱和干涉光谱

该传感器采用3μm厚的镍箔为振膜,其密度为8 800 kg/m3,振膜的共振频率约为8 000 Hz;采用的PIN光电探测器的光电转换系数为0.9 mA/mW,电流电压转换电阻为100 kΩ。该传感器采用的光源的光谱如图9(a)所示,其波长为1 552.27 nm,入射光功率为0.57 mW。图9(b)所示为该传感器归一化干涉光谱,从图中可以得到干涉对比度为0.977。取空气的折射率为1,光纤端面的反射率为4%。由以上数据,可以计算得到,该传感器的理论灵敏度约为248.8 mV/Pa。

图10所示为光纤法珀腔声传感器样品频率响应曲线和动态范围的测试结果。由图10(a)可知,样品在1 kHz处的灵敏度为216 mV/Pa,该值接近于理论计算值,表明理论分析的结果正确可信。此外,该传感器在50 kHz～6.3 kHz频率范围内,频率响应曲线的平坦度小于±1.5 dB,具有比较平坦的频率响应特性,与谐响应分析也是一致的。图10(b)是光纤法珀腔声传感器样品对1 kHz声波的输出信号,该声波信号是由114 dB标准声源发出,从测试结果可以看出,在114 dB声压下,振膜的振幅引起的相位变化超过了一个线性区间范围,从而导致输出信号出现凹陷失真。从图10(b)中可以估计出此传感器最大不失真信号的峰值约为1.8 V,该值对应的声压为109.4 dB,与理论分析的110 dB是一致的。

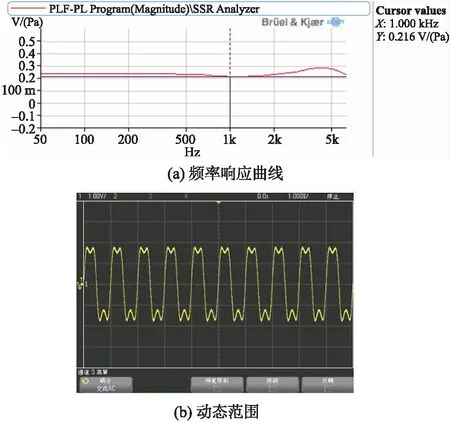
图10 光纤法珀腔声传感器样品频率响应曲线和动态范围测试结果

6 结论

本文对光纤法珀腔声传感器的敏感机理进行了分析,并对振动模态和谐响应进行了有限元仿真分析,分析了光纤法珀腔声传感器的灵敏度与材料、结构、光学、电学参量的关系,以及它的动态范围。

通过理论和仿真分析可知,光纤法珀腔声传感器工作在单色光源情况下,初始相位需要在正交点附近,然后利用干涉光谱的一段线性区间实现声波信号的解调。为了使光纤法珀腔声传感器具有良好的频率响应特性,根据模态分析和谐响应分析,传感器的频率上限要尽可能远离一阶共振频率。光纤法珀腔声传感器的灵敏度与干涉光的强度和干涉对比度、光波长、振膜的面密度、振膜的共振频率、以及转换电阻相关。在研制光纤法珀腔声传感器时,根据实际应用需求,确定这些参数。最后制作了光纤法珀腔声传感器样品,对理论分析进行验证,结果表明,实验结果与理论分析是一致的。